студ ивт 22 материалы к курсу физики / belonuchkin_ve_zaikin_da_tsipeniuk_ium_kurs_obshchei_fiziki

поэтому фактически скорость звука в выражении (8.25) является средней скоростью звуковых волн в кристалле, но принципиального значения это не имеет.

Теперь надо выяснить, до какой максимальной частоты мы должны интегрировать. С одной стороны, в единице объема кристалла имеется конечное число частиц и пусть оно равно , а это, согласно общим принципам механики, означает, что всего может быть 3 степеней свободы, т. е. 3 различных колебательных мод или 3 фононов. Но, с другой стороны, мы знаем, какова плотность состояний трехмерной системы: как следует из формулы (6.17), для фотонов число уровней в единичном интервале энергий 2 2 3 . Как выше было показано, при переходе к фононам надо вместо скорости света подставить скорость звука и умножить на 3/2. Чтобы найти полное число состояний в единице объема, надо проинтегрировать это выражение от 0 до . В дебаевском приближении эта максимальная частота называется дебаевской частотой Д и можно записать

Для простой кубической решетки 1 3 и поэтому дебаевская частота равна

Итак, дебаевская частота пропорциональна 1 3, фактически она очень близка к величине частоты на границе зоны Бриллюэна и поэтому можно при всех оценках считать ее равной . Дебаевской частоте можно поставить в соответствие некую характеристическую температуру — температуру Дебая :

Таким образом, дебаевской частоте соответствуют колебания с длиной волны порядка межатомного расстояния. Следует отдавать себе отчет, что температура Дебая является параметром модели, а не физической характеристикой вещества. Температура Дебая, как правило, лежит в области 200–500 K, хотя есть вещества и с очень высокой и очень низкой температурой Дебая. Например, у бериллия она равна 1440 К, а у цезия 30 K, у бария 74 K.

ласти температур возбуждаются лишь длинноволновые фононы, оптические волны (даже если таковые могут быть) не возбуждаются при низкой температуре: на их возбуждение при не хватает тепловой энергии. Поэтому интегрирование в формуле (8.25) можно продлить до бесконечности, а в таком случае имеем

и соответственно теплоемкость кристалла при низких температурах должна быть пропорциональна кубу температуры:

Мы получили так называемый закон Дебая для низкотемпературной теплоемкости твердого тела. Легко качественно показать, почему получается такая зависимость от температуры.

Рассмотрим импульсное пространство в изотропном случае (рис. 8.8).

новым вектором, длина которого меньше , имеют энергию, равную классической ее величине Б , а моды с волновыми векторами в интервале между и Д не возбуждаются вообще. Из 3 возможных мод доля возбуждаемых колебаний составляет 3, поскольку эта величина равна отношению объема внутренней сферы радиуса к объему сферы радиусом

Д . Для энергии в этом случае имеем Б 3 3, и соответственно теплоемкость будет подчиняться кубическому

закону.

Теперь рассмотрим другой предельный случай — высокие температуры ( ). Это классическая область, возбуждаются практически только дебаевские фононы, так как это фононы максимально возможной частоты, а тепловая энергия много большеД согласно нашему предположению. Тот факт, что возбуждаются приемущественно фононы максимальной частоты, связано с зависимостью плотности состояний от волнового вектора — она пропорциональна 2 (см. формулу (6.16)). Энергия кристалла

Следующим этапом нашего рассмотрения является теплопроводность твердого тела. Напомним, что мы сейчас рассматриваем только роль решетки в тепловых процессах, и поэтому речь будет идти о решеточной теплопроводности. Механизм переноса тепловой энергии атомными колебаниями в основе своей очень прост. Атомы в твердом теле тесно связаны друг с другом. Если при нагревании некоторого участка твердого тела какой-либо атом начинает колебаться около своего положения равновесия в решетке, то при своем движении он толкает соседние атомы, которые в свою очередь передают это движение своим соседям, и т. д. Кинетическая энергия колебания атомов переносится, таким образом, от нагретого участка к более холодному.

Однако как мы показали, возбуждение кристаллической решетки удобно описывать на языке фононов. Поэтому теплопроводность очень легко понять, если рассматривать кристалл как «ящик с фононами». Пусть на одном конце твердого тела поддерживается температура 1, а на другом 2, причем 2 1. Это означает, что на левом конце (там, где температура равна1) плотность фононов меньше, чем на правом конце. Ясно, что фононы с правого конца будут диффундировать в левый конец, пытаясь выравнять плотность фононов по всему телу. При своем перемещении от теплого конца к холодному фононы переносят тепло, которое отводится от холодного конца, если его поддерживать при постоянной температуре. Пришедшие фононы просто «исчезают», так как их число определяется температурой. На горячем конце фононы «зарождаются», ибо поддерживать постоянную температуру можно, только подводя тепло к телу.

Представление о тепловом движении в твердом теле как о газе фононов дает нам возможность вычислить теплопроводность твердого тела точно так же, как это делается в обычных газах. Согласно молекулярно-кинетической теории газов коэффициент теплопроводности равен

где — теплоемкость единицы объема газа, — средняя длина свободного пробега молекул газа, — их средняя тепловая скорость. Так как средней скоростью фононов можно считать скорость звука и теплоемкость нам уже известна, все, таким образом, определяется длиной свободного пробега фононов, которая ограничивается столкновениями и равна

В этом выражении — концентрация частиц, — сечение рассеяния.

Вкинетической теории газов причиной рассеяния частиц газа

иискривления их траекторий является факт конечности размеров молекул. В случае твердого тела длина свободного пробега обусловлена нарушениями правильности его кристаллической решетки. Причиной нарушения периодичности решетки могут быть как различные дефекты кристалла, так и сами фононы. Когда атом отклоняется от своего равновесного положения при прохождении фонона, то другой фонон, встречая отклоненный атом, испытывает сильное столкновение и резко меняет свой путь точно так же, как если бы на пути фонона встретился примесный атом. Так сами фононы мешают своему собственному движению как молекулы в газе.

Рассмотрим вначале теплопроводность твердого тела в области высоких температур. Высокие температуры в твердом теле означают, что . В этой области температур теплоемкость

фононного газа постоянна и равна 3 Б , все фононы движутся согласно дебаевской модели со скоростью звука и надо найти, как длина свободного пробега зависит от температуры. При температурах, б´ольших дебаевской, возбуждаются практически лишь фононы максимальной энергии. Как мы уже выяснили, в этой области справедлив классический подход, т. е. мы можем считать, что на каждую степень свободы приходится энергияБ , а это значит, что их среднее число может быть оценено как

Сечение рассеяния определяется размером неоднородности плотности в кристалле, вызванной фононом, но при высоких температурах они все практически одинаковы (одной частоты), а это значит, что сечение рассеяния — практически постоянная величина и поэтому длина свободного пробега

Следовательно, коэффициент теплопроводности зависит от температуры как

Теперь посмотрим, что происходит при уменьшении температуры. Теплоемкость начинает уменьшаться в соответствие с дебаевским законом как 3, но наиболее существенным фактором оказывается рост длины свободного пробега из-за уменьшения числа фононов с температурой и поэтому теплопроводность начинает возрастать.

Однако по мере уменьшения температуры процесс роста длины свободного пробега должен прекратиться либо за счет

476 Динамика атомов кристаллической решетки. Фононы [ Гл. 8

рассеяния на примесях либо на дефектах структуры, либо стать равным размерам кристалла. В этом случае

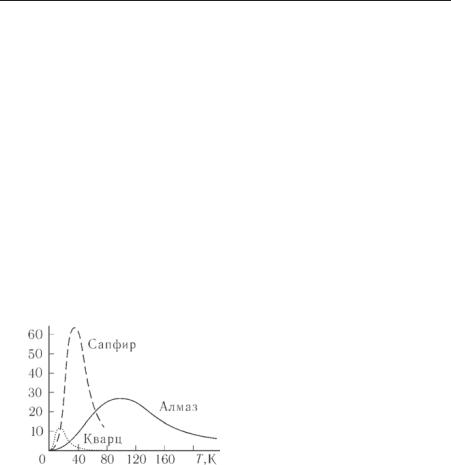
а это значит, что при низких температурах теплопроводность уменьшается как 3. Резкое уменьшение решеточной теплопроводности кристаллов при низких температурах приводит к появлению максимума коэффициента теплопроводности. Экспериментальные данные, приведенные на рис. 8.10 для некоторых диэлектриков (кварца, синтетического сапфира и алмаза), качественно полностью подтверждают температурную зависимость теплопроводности, рассмотренную нами на основе фононной модели.

В совершенных кристаллах значение в максимуме может быть очень большим. Так, например, у сапфира, как это видно из рис. 8.10, при 40 К коэффициент теплопроводности60 Вт/(м град), что больше теплопроводности меди при этих температурах.

, Âò/(ì . ãðàä)

, Âò/(ì . ãðàä)

И, наконец, рассмотрим качественно теплопроводность аморфных тел. Для аморфных тел характерно отсутствие дальнего порядка и, грубо говоря, их «кристаллиты» имеют размеры порядка атомных. Поэтому рассеяние на «границах» этих кристаллитов преобладает при всех температурах, а значит длина свободного пробега фононов . Поэтому у аморфных веществ в области низких температур коэффициент теплопроводности ведет себя как 3, а затем имеет постоянное значение. Для иллюстрации указанной закономерности на рис. 8.11 приведены результаты температурной зависимости коэффициента теплопроводности для ряда стекол: 1 — плавленный кварц, 2 — боросиликатный кронглас, 3 — пирекс, 4 — тюрингское стекло. Следует обратить внимание, что экспериментальные данные приведены в логарифмическом масштабе.

8.5 ] Задачи 477

возбуждению фонона в центре зоны Бриллюэна. Для NaCl упругая константа (жесткость цепочки) 15 Н/м.

Решение. Так как NaCl образует при кристаллизации гранецентрированную кубическую решетку, то можно считать, что ее фононный спектр описывается моделью одномерной двухатомной цепочки. Это означает, что в этом кристалле могут возбуждаться как акустические, так и оптические колебания.

частота является максимальной частотой колебаний для двухатомной линейной цепочки. Для NaCl приведенная масса равна

Длина волны оптических колебаний при 0 равна

2 2 2 0,06 мм 60 мкм,

что и требовалось показать.

2. В кристалле поваренной соли NaCl при температуре 10 K тепло-

емкость единицы объема 830 10 4 Дж/(м3 К). Оценить скорость звука в кристалле и его дебаевскую температуру. Постоянная решетки NaCl равна0,3 нм.

520 K.

3.Одинаковые массы свинца 207Pb и кремния 28Si охлаждают с помощью жидкого гелия (температура кипения гелия равна при нормальном давлении

4,2 К) от температуры 1 20 K до 2 4,2 K. Оценить отношение масс жидкого гелия, необходимых для охлаждения свинца и кремния, если известно, что дебаевские температуры равны: Pb 95 K и Si 645 K. Теплоемкостью электронов пренебречь.

Решение. Так как начальная температура много меньше температур Дебая обоих веществ, то справедливо низкотемпературное приближение. Теплота, отбираемая при охлаждении у тел, в соответствии с формулой (8.30) равна

Используя формулы (8.27) и (8.29), это выражение можно записать в виде

Так как масса кристалла , где — атомная масса, то

1

3

Так как масса испарившегося гелия пропорциональна величине отбираемой у тела теплоты, то окончательно имеем:

4. Свободное покоящееся ядро иридия-131 переходит из возбужденного состояния с энергией 129 кэВ в основное, испуская -квант. Найти энергию излучаемого -кванта и энергию отдачи ядра.

Решение. Поскольку энергия возбуждения атомных ядер всегда много меньше энергии покоя атомного ядра, задачу можно решать в нерелятивистском приближении. Из законов сохранения энергии и импульса следует:

Энергия излучаемого кванта отличается от энергии перехода на эту же величину.

5. При комнатной температуре примерно 20 % -распадов 119Sn в соединении BaSnO3 происходит без отдачи (эффект Мёссбауэра). Оценить, какой должна быть толщина источника, чтобы в нем не происходило заметного погло-

щения мессбауэровских -квантов. Плотность BaSnO3 3 г/см3, содержание изотопа 119Sn в естественной смеси 8 %, энергия -квантов 24 кэВ.

Решение. При прохождении через вещество интенсивность излучения уменьшается с расстоянием по экспоненциальному закону

0

Условие отсутствия заметного поглощения определяется неравенством

Авогадро, — молекулярная масса BaSnO3, которая равна 304. Самопоглощение мессбауэровских -квантов — резонансный процесс, сечение которого описывается формулой Брейта–Вигнера

При этом мы учли, что для -квантов соотношение между импульсом и волновым вектором линейно , а энергия -кванта , т. е. .

Таким образом, получаем, что толщина источника должна удовлетворять

Г л а в а 9

ЭЛЕКТРОНЫ В КРИСТАЛЛАХ

С точки зрения электрических свойств все твердые тела разделяются на металлы (хорошие проводники электричества), полупроводники и изоляторы (плохие проводники электричества). Одним из принципиальных вопросов теории твердого тела является вопрос об основном и возбужденных состояниях электронной подсистемы, т. е. фактически вопрос о том, почему одни химические элементы в кристаллическом состоянии оказываются хорошими проводниками, другие — изоляторами, третьи — полупроводниками, электрические свойства которых резко зависят от температуры.

Интуитивно ясно, что энергетические уровни изолированных атомов искажаются, когда большое число атомов приводится в твердом теле в тесный контакт. Полная энергия электронной подсистемы состоит из кинетической энергии электронов, потенциальной энергии электронов в электростатическом поле, создаваемом ионами, и энергией кулоновского взаимодействия электронов друг с другом. Вопрос заключается в том, в каких случаях можно пренебречь взаимодействием электронов с решеткой, а когда это взаимодействие существенно.

9.1. Электроны в металле

Простейшее приближение состоит в пренебрежении в выражении для полной энергии всеми членами, кроме кинетической энергии. Это так называемая модель свободных электронов, которая удачно объясняет электрические и магнитные свойства твердых тел, в первую очередь металлов. Она исходит из представления, что металл содержит свободные электроны, способные перемещаться по всему объему.

Принятая аппроксимация позволяет рассматривать систему как газ свободных электронов. Далее надо учесть, что электроны описываются статистикой Ферми–Дирака, т. е. подчиняются принципу Паули. Из принципа Паули следует, что в случае свободных электронов основным состоянием должно быть такое, в котором низшие одноэлектронные уровни полностью заполнены вплоть до некоторой энергии, называемой уровнем Ферми.

480 Электроны в кристаллах [ Гл. 9

В случае газа свободных электронов энергия состояния с волновым вектором имеет вид

В этом случае в -пространстве электроны занимают сферу, о поверхности которой говорят как о поверхности Ферми. Радиус Ферми Ф — максимальное значение волнового вектора электронов — определяется из условия, что состояния внутри этой сферы заполнены электронами, по паре электронов с противоположными спинами на каждом уровне. Объем сферы радиусом

где — плотность электронов. Соответственно фермиевский импульс (максимальный импульс электронов) равен

а величина Ф Ф называется фермиевской скоростью. Тем самым уровень Ферми или энергия Ферми Ф — максимальная энергия электронов, отсчитанная от нулевой кинетической энергии — следующим образом определяется через их концентрацию:

где мы учли, что 3.

При температурах, меньших температуры вырождения, электронная подсистема кристалла должна рассматриваться в рамках квантовой механики, так как тепловая энергия не может существенно исказить характер заполнения энергетических уровней электронами. В другом предельном случае она является чисто классическим объектом. Легко оценить величину температуры вырождения, исходя из соотношения неопределенностей: так как расстояние между частицами 1 3, то частицы тем самым локализованы в объеме такого размера; минимально возможный