
Проблемы обеспечения надежности и качества приборов, устройств и систем
.pdf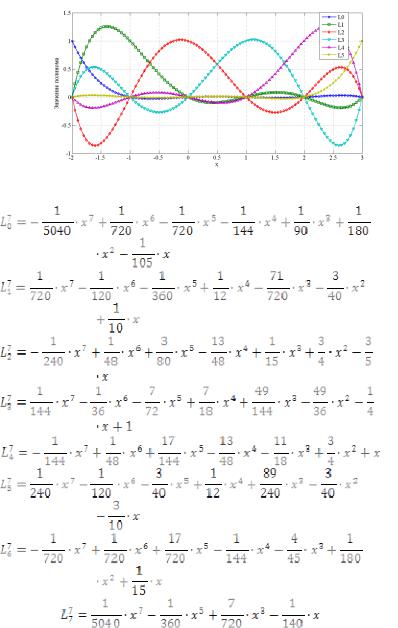
Рис. 2. Ортогональные полиномы Лагранжа 5-го порядка
(5)
101
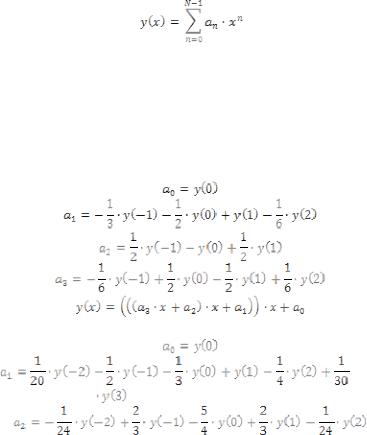
Для получения алгоритма нахождения коэффициентов интерполяции по отсчетам на старой частоте дискретизации следует воспользоваться выражением (6). В выражении (6) x – временное положение отсчета в произвольный момент времени (на новой частоте дискретизации) относительно ближайшего отсчета на старой частоте дискретизации, нормированное относительно старого значения интервала дискретизации. Значение x изменяется в диапазоне 0..1.
(6)
Приравняв выражения (1) и (6) и сгруппировав слагаемые определенным образом, можно однозначно выразить коэффициенты an через отсчеты на старой частоте дискретизации. Так, выражения
(7)-(9) дают математическое описание алгоритма нахождения коэффициентов интерполяции по отсчетам на старой частоте дискретизации для ресэмплеров 3-, 5-, 7-го порядков соответственно.
(7)
(8)
102
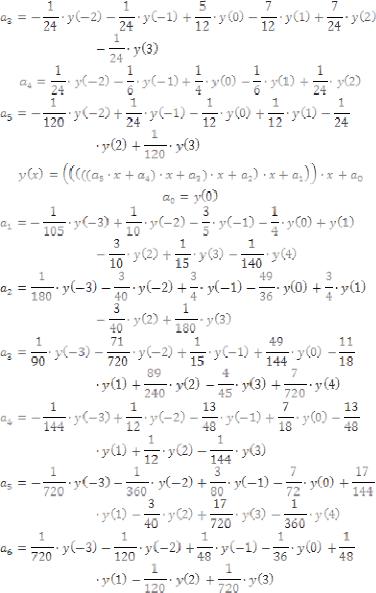
(9)
103
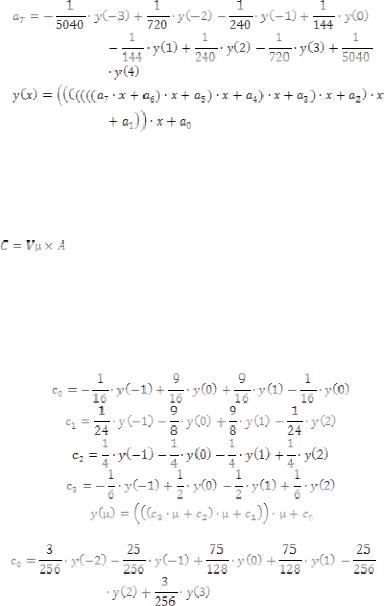
Кроме приведенной выше несимметричной формы представления коэффициентов интерполяции (7-9) существует симметричная форма [10]. Для вывода выражений в симметричной форме можно воспользоваться (10).
(10)
Выражения для нахождения коэффициентов интерполяции 3-, 5, 7-го порядков по дискретным отсчетам в симметричной форме приведены ниже (11-13). При этом значение нормированного временного положения µ изменяется в диапазоне -0.5..0.5.
(11)
(12)
104
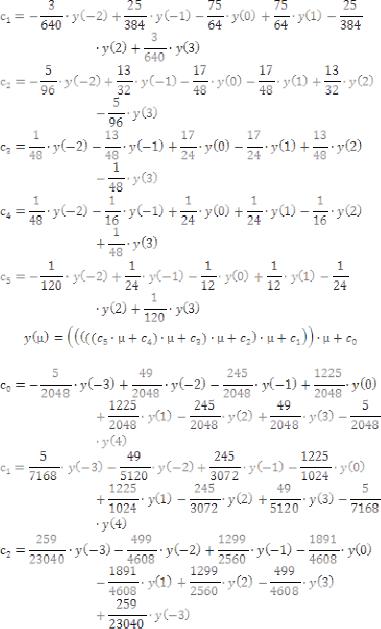
(13)
105
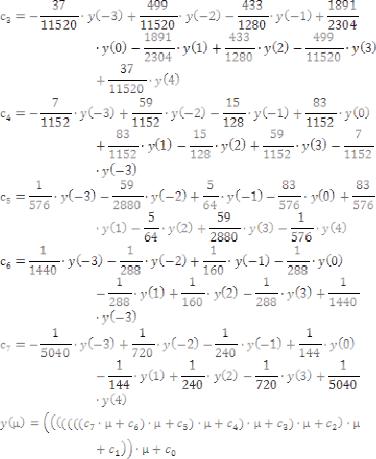
Таким образом, по дискретным отсчетам можно найти значение сигнала в произвольный момент времени. С практической точки зрения удобнее использовать выражения (11-13) для нахождения коэффициентов интерполяции по дискретным отсчетам. Это связано с удобством реализации на ПЛИС цифровых фильтров, реализующих выражения (11-13), или устройств на степенях числа 2.
Теоретическая оценка уровня нелинейных искажений, вносимых в сигнал.
Для оценки качества передискретизации было принято решение описать аналитически импульсную и частотную характеристики ресэмплеров различных порядков. С помощью
106
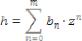
данных характеристик можно оценить уровень амплитудночастотных искажений ресэмплера.
Импульсная характеристика ресэмплера обладает следующими свойствами:
-является непрерывной, кусочно-заданной функцией, имеющей конечную длительность;
-число интервалов составляет n+1, где n – порядок интерполяции;
-на каждом временном интервале описывается полиномом, порядок которого не превышает порядок интерполирующего полинома.
На каждом временном интервале импульсная характеристика ресэмплера m-го порядка описывается выражением (14).
(14)
где an – коэффициент полинома, z – нормированное временное значение.
Для получения коэффициентов полинома импульсной характеристики ресэмплера (14) необходимо решить систему линейных уравнений с числом неизвестных, превышающих порядок ресэмплера на 1.
В табл. 1-3 представлены коэффициенты полинома (14) для ресэмплеров различных порядков.
Таблица 1 Коэффициенты полинома импульсной характеристики ресэмплера
3-го порядка
Коэффициенты полинома |
Интервалы |
|
z [0..1] |
z [1..2] |
|
b0 |
1 |
1 |
b1 |
–1/2 |
–11/6 |
b2 |
–1 |
1 |
b3 |
1/2 |
–1/6 |
|
|
|
107
Таблица 2 Коэффициенты полинома импульсной характеристики ресэмплера
5-го порядка
Коэффициенты |
Интервалы |
|
|
полинома |
z [0..1] |
z [1..2] |
z [2..3] |
b0 |
1 |
1 |
1 |
b1 |
–1/3 |
–13/12 |
–137/60 |
b2 |
–5/4 |
–5/8 |
15/8 |
b3 |
5/12 |
25/24 |
–17/24 |
b4 |
1/4 |
–3/8 |
1/8 |
b5 |
–1/12 |
1/24 |
–1/120 |
|
|
|
|
Таблица 3 Коэффициенты полинома импульсной характеристики ресэмплера
7-го порядка
Коэффициенты |
Интервалы |
|
|
|
полинома |
z [0..1] |
z [1..2] |
z [2..3] |
z [3..4] |
b0 |
1 |
1 |
1 |
1 |
b1 |
–1/4 |
–141/180 |
–87/60 |
–9801/3780 |
b2 |
–49/36 |
–189/180 |
–7/36 |
3283/1260 |
b3 |
49/144 |
231/240 |
889/720 |
–6769/5040 |
b4 |
7/18 |
0 |
–7/9 |
147/378 |
b5 |
–7/72 |
–7/40 |
77/360 |
–161/2520 |
b6 |
–1/36 |
1/20 |
–1/36 |
7/1260 |
b7 |
1/144 |
–1/240 |
–1/720 |
–1/5040 |
Для расчета частотной характеристики ресэмплера необходимо найти Фурье-образ импульсной характеристики ресэмплера n-го порядка. На рис.3 представлено семейство амплитудно-частотных характеристик ресэмплеров 3-, 5-, 7-го порядков. Нормировка частотной оси осуществляется относительно исходной частоты дискретизации Fs. По рассчитанным частотным характеристикам ресэмплера можно определить:
-динамический диапазон (степень подавления зеркальных спектральных составляющих);
-неравномерность в полосе пропускания;
-уровень нелинейных частотных искажений, связанный с отражением копий спектра дискретного сигнала при передискретизации.
108
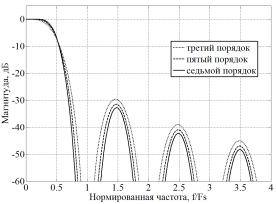
Рис. 3. Семейство амплитудно-частотных характеристик ресэмплеров
Литература
1.Прокис, Дж. Цифровая связь [Текст] / Дж. Прокис. – М.: Радио и связь, 2000. - 800 с.
2.Скляр, Б. Цифровая связь. Теоретические основы и практическое применение [Текст] / Б. Скляр. - М.: Издательский дом «Вильямс», 2007. - 1104 с.
3.Nezami, Mohamed RF Architectures & Digital Signal Processing Aspects of Digital Wireless Transceivers [Text] / M. Nezami, 2003. - 512 с
4.Шахнович, И. Современные технологии беспроводной связи [Текст] / И. Шахнович. - М.: Техносфера, 2006. - 288 с.
5.Спажакин, М.И. Оценка искажений при передискретизации цифрового сигнала с использованием фильтра Фарроу [Текст] / М.И. Спажакин, В. Д. Репников, А. Б. Токарев // Вестник Воронежского государственного технического университета. - 2013. - Т.9. - №6.3. - С. 26 – 29.
6.Peled, A. A New Approach to the Realization of Nonrecursive Digital Filters [Текст] / A. Peled, B.Liu // IEEE Trans. Audio and Electroacoustics, 1973. - vol. AU-21. - №6. - pp. 477–485.
7.Спажакин, М.И. Синтез нерекурсивных цифровых фильтров без умножителей [Текст] / А.В. Муратов, М.И. Спажакин, А. Б. Токарев // Вестник Воронежского государственного технического университета. - 2014. - Т.10. - №1. - С. 88 – 91.
109
8.Рабинер, Л. Теория и применение цифровой обработки сигналов [Текст] / Л. Рабинер, Б.Гоулд. - М.: Мир, 1978. - 848 с.
9.Фильтр Фарроу на примере фильтра третьего порядка. Ресэмплинг сигналов [Электронный ресурс]. Режим доступа: http://www.dsplib.ru/content/farrow/farrow.html, свободный (дата обращения: 20.10.2013).
10.Olli Niemitalo. Polynomial Interpolators for High-Quality Resampling of Oversampled Audio [Электронный ресурс]. Режим доступа: http://yehar.com/blog/wp-content/uploads/2009/08/deip.pdf,
свободный (дата обращения: 20.10.2013).
11.Discrete-Time signal processing Alan V. Oppenheim, Ronald W. Schafer, John R. Buck, PRENTICE HALL – second edition 1998
12.Y. C. Lim and S. R. Parker, FIR filter design over a discrete powers-of-two coefficient space, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP-31, pp. 583–591, June 1983.
Воронежский государственный технический университет
110
