3683

Затем локальный коэффициент теплоотдачи в СКФ, соответствующий температуре (z), определялся как

Отметим, что здесь коэффициент теплоотдачи определяется относительно среднемассовой температуры, поэтому, вообще говоря, может не совпадать со значениями, находимыми из других критериальных уравнений. Также коэффициент теплоотдачи непосредственно рассчитывается по среднемассовой температуре и температуре стенки, полученных в предыдущем разделе.

Локальное число Нуссельта определялось на основании значения (3.2) по формуле

Это значение также определялось для коэффициента теплопроводности, взятого при среднемассовой температуре.

В результате для каждой комбинации параметров найдена таблица (Nu1.i, i, ст.i, j, k ) зависимости числа Нуссельта от температур потока СКФ и

стенки трубки, давления СКФ и коэффициента теплоотдачи в теплоносителе. Некоторые результаты расчетов по формулам (3.1-3.3) представлены на

рис. 10-12.

Проведено также сравнение с расчетом теплоотдачи в околокритической области (рис. 10). Как видно из сравнения, выход в околокритическую область приводит к значительному немонотонному снижению коэффициента теплоотдачи. Поэтому режим работы криогенной системы следует выбирать таким образом, чтобы рабочая зона оставалась в закритической области давлений.

Рис. 10. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-кислорода при закритическом давлении СКФ и сравнение с данными для околокритического давления (10 МПа)

80

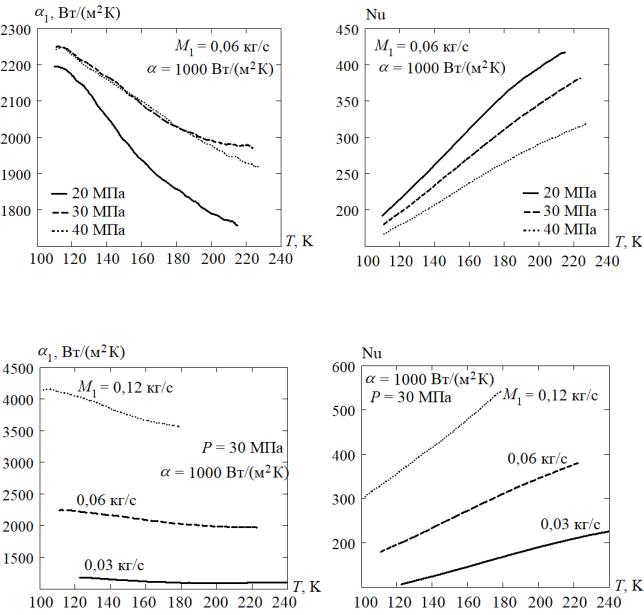
Рис. 11. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-кислорода при различном массовом расходе СКФ

Рис. 12. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-кислорода при различном коэффициенте

Для получения критериального уравнения была использована мультипликативная модель, в которую были включены все обычно используемые факторы:

нее по теплоемкости число Прандтля, часто используемое [8] при построении критериального уравнения для СКФ.

Коэффициенты i находились регрессионным анализом линеаризованной модели, полученной логарифмированием равенства (3.4). Анализ показал, что

81

существенно незначимыми. В результате отсеивания этих коэффициентов модель сократилась до вида

В данной модели все коэффициенты показали высокий уровень значимости, относительная ошибка определения натуральных (не логарифмированных) значений числа Нуссельта составила: максимальное значение 3 , среднее значение 1 . Окончательное полученное выражение числа Нуссельта для СКФкислорода имеет вид:

Корреляция полученных в вычислительном эксперименте и рассчитанных по формуле (3.6) значений числа Нуссельта показана на рис. 13.

Как видно, полученные данные показывают очень хорошую корреляцию с уравнением (3.6).

Отметим, что в высокотемпературном пределе последние три сомножите-

ля в левой части равенства (3.6) стремятся к единице, а Pr Pr, в результате уравнение (3.6) показывает хорошее согласие с классической формулой ДиттусаБолтера, что важно для расчетов в широкой области температур. Это также подтверждает достоверность формулы (3.6). Отличие в числовом коэффициенте связано с тем, что для рассматриваемых чисел Рейнольдса сама формула Дит- туса-Болтера неточна, а также наша формула построена для диапазона высоких давлений.

Рис. 13. Сравнение чисел Нуссельта для СКФ-кислорода, полученных в вычислительном эксперименте и по формуле (3.6)

82

4 Вычислительный ксперимент и аппроксима ия ко ффи иента теплоотдачи азота

Вторая серия расчетов проводилась для СКФ-азота при том же наборе параметров, что и для кислорода. Результаты обработки вычислительного эксперимента по формулам (2.6-2.8) показали, что влияние давления, массового расхода СКФ и коэффициента теплоотдачи для СКФ-азота качественно совпадает с аналогичными результатами, полученными для СКФ-кислорода.

Результаты обработки данных вычислительного эксперимента по азоту по формулам (3.1-3.3) приведены на рис. 14-16.

Рис. 14. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-азоте при различном давлении СКФ

Рис. 15. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-азоте при различном массовом расходе СКФ

83

Рис. 16. Температурная зависимость коэффициента теплоотдачи и числа Нуссельта в СКФ-азоте при различном коэффициенте

Для аппроксимации зависимости числа Нуссельта в азоте также использовалась модель (3.4), но потребовалось учесть зависимость коэффициентов модели от давления, как в уравнении Краснощекова и Протопопова [3]. Использовалась линейная зависимость от давления. В рамках регрессионного анализа установлены те же незначимые коэффициенты, что и в случае кислорода, и дополнительно коэффициент 5. Также значимую зависимость от давления показал только коэффициент 7. Результирующее критериальное уравнение для азота имеет вид:

Здесь относительная ошибка определения натуральных значений числа Нуссельта составила максимальное значение 4 , среднее значение 1,5 .

Корреляция полученных в вычислительном эксперименте и рассчитанных по формуле (3.6) значений числа Нуссельта показана на рис. 17.

Рис. 17 свидетельствует, что полученные данные показывают хорошую корреляцию с уравнением (3.6). Это уравнение также показывает хорошее соответствие с высокотемпературным пределом в форме уравнения ДиттусаБолтера. Отметим, что специфические коэффициенты в уравнении (4.1) для кислорода оказались существенно другими, чем для кислорода в уравнении (3.6). Поскольку данные уравнения получены в одном вычислительном эксперименте и отличались только теплофизическими зависимостями свойств от температуры, то это различие можно считать достоверным. Данное различие подтверждает мнение [3], что критериальное уравнение в псевдокритической области температур существенно зависит от природы и типа вещества.

84

Рис. 17. Сравнение чисел Нуссельта для СКФ-азота, полученных в вычислительном эксперименте и по формуле (4.1)

Отметим, что в критериальные уравнения (3.6), (4.1) не вошел в явном виде фактор коэффициента теплоотдачи с теплоносителем, его влияние автоматически учитывается через самосогласованное формирование температуры стенки в процессе теплопереноса. Это означает, что в рассматриваемой закритической области формируется автомодельный режим теплоотдачи из СКФ, позволяющий использовать универсальные зависимости вида (3.6), (4.1) для широкого диапазона давлений и массовых расходов.

Литература

1.Кутателадзе С. С. Теплопередача и гидродинамическое сопротивление. – М.: Энергоатомиздат, 1990. – 367 с.

2.Алексеев В. П., Вайншетейн . Е., ерасимов П. В. Расчет и моделирование аппаратов криогенных установок. – Л.: Энергоатомиздат, 1987. 280 с.

3.Петухов Б. С., енин Л. ., Ковалев С. А. Теплообмен в ядерных энергетических установках. М.: Атомиздат, 1974. 408 с.

4.Pioro Igor L., Duffey Romney B. Experimental heat transfer in supercritical water flowing inside channels (survey) // Nuclear Engineering and Design. 2005. V. 235. P. 2407-2430.

5. Huang Dan, ub Zan, Sunden Bengt, Li ei. A brief review on convection heat transfer of fluids at supercritical pressures in tubes and the recent progress // Applied Energy. 216. V. 162.

P.494-505.

6.Роуч П. Вычислительная гидродинамика. – М.: Мир, 1980. – 618 с.

7.Павловский В. А., Никущенко Д. В. Вычислительная гидродинамика. Теоретические основы. – СПб: Лань, 2018. – 368 с.

8.Petrov N. E., Popov V. N. Heat transfer and hydraulic resistance with turbulent flow in a tube of water under supercritical parameters of state // Thermal Engineering. 1988. V. 35. P. 557580.

9.Cheng He, Yonglin u, Yunzhun Fu. Experimental and simulation investigation on heat transfer characteristics of supercritical nitrogen in a new rib tube of open rack vaporizer // International ournal of Refrigeration. 2019. V. 111. P. 103-112.

85

SIMULATION OF HEAT AND MASS TRANSFER

IN THE FLO OF SUPERCRITICAL NITROGEN AND

OYGEN IN A TUBE BY THE FINITE ELEMENT METHOD S. V. Borodkin, I. L. Bataronov, A. V. Ivanov, V. I. Ryazhskikh

1Military Educational and Scientific Center of the Air Force “N.E. Zhukovsky

and Yu. A. Gagarin Air Force Academy”, Voronezh

2Voronezh State Technical University

A computational experiment was performed using the finite element method to determine the temperature and velocity fields in a supercritical turbulent flow of oxygen and nitrogen. Heat transfer with the environment was modeled using the Newton-Richman equation with a constant heat transfer coefficient. The distributions along the flow of the mean-enthalpy temperature, the wall temperature, and the linear density of the heat flow through the wall are found. Based on these data, the local heat transfer coefficients and the Nusselt number are calculated. The criterion equations for the local Nusselt criterion in nitrogen and oxygen in the over-critical region are constructed.

Keywords: modeling, turbulent heat and mass transfer, criterion equation, heat transfer coefficient.

86

УДК 539.21, 538.915

ФИЗИКО-МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ЭНЕР ЕТИЧЕСКО О СПЕКТРА СФЕРИЧЕСКИХ ЕТЕРОСТРУКТУР

В. В. Филиппов, А. О. Золотухина

Липецкий государственный педагогический университет им. П. П. Семенова-Тян-Шанского wwfilippow@mail.ru

Выполнено моделирование энергетического спектра слоистой структуры в сферических неоднородных квантовых точках. В работе представлен случай радиальносимметричного распределения слоев с различной величиной работы выхода электронов. Теоретический расчет реализован в рамках нерелятивистской теории квантовой механики.

Ключевые слова: энергетический спектр, квантовая точка, уравнение Шрёдин-

гера.

Внастоящее время наночастицы широкого диапазона строения, размеров

иструктуры находят все большее практическое использование в химической технологии, строительстве, машиностроении, электронике, медицине и других отраслях [1, 2]. Перспективным методом управления параметров квантовых точек (КТ), а также стабилизации их структуры является нанесение различных защитных нанотекстур или химически активных пленок [3, 4].

С целью анализа влияния покрытия на энергетические свойства КТ рассмотрим одноэлектронное стационарное уравнение Шрёдингера для квантовой ямы со сферической симметрией. В приводимых ниже расчетах будем полагать распределение электронной плотности по угловым компонентам симметричным, следовательно анализируемое решение реально описывает одноэлектронное состояние ( =0).

Врассматриваемом случае гамильтониан примет вид [5, 6]:

Соответственно, уравнение Шрёдингера удобно представить в виде:

когда сферически симметричная однородная наночастица, накрывается тонким защитным ( активным) нанослоем. При переходе из одного материала в другой учтем изменение физических свойств: m1 и m2 – эффективные массы электронов в слоях КТ (m0 – масса свободного электрона); 1 и 2 – работы выхода контактирующих материалов (рис. 2).

В силу рассматриваемой симметрии, задачу для КТ, как это показано в работах [3, 4], удобно решать в сферической системе координат ( , , ).

87

С учётом постановки физической задачи, уравнение распадается на три:

88

раничные условия, вытекающие из непрерывности волновой функции и плотности потока, в данном случае принимают вид:

ψ( = 0) ≠ 0,

ψ ( = ∞) = 0,

89