11. Энергия заряженного проводника и конденсатора. Плотность энергии электростатического поля.

1. Энергия заряженного проводника и конденсатора.

Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен  , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная  . Но потенциал электростатического поля данного проводника в бесконечности равен нулю  . Тогда

При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.

Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

Применяя соотношение  , можно получить следующие выражения для потенциальной энергии W:

Для заряженного конденсатора разность потенциалов (напряжение) равна  поэтому соотношение для полной энергии его электростатического поля имеют вид: 11. Энергия заряженного проводника и конденсатора. Плотность энергии электростатического поля.

1. Энергия заряженного проводника и конденсатора.

Если уединенный проводник имеет заряд q, то вокруг него существует электрическое поле, потенциал которого на поверхности проводника равен  , а емкость - С. Увеличим заряд на величину dq. При переносе заряда dq из бесконечности должна быть совершена работа равная  . Но потенциал электростатического поля данного проводника в бесконечности равен нулю  . Тогда

При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.

Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

Применяя соотношение  , можно получить следующие выражения для потенциальной энергии W:

Для заряженного конденсатора разность потенциалов (напряжение) равна  поэтому соотношение для полной энергии его электростатического поля имеют вид:

2. Плотность энергии электростатического поля.

Это физическая величина, численно равная отношению потенциальной энергии поля, заключенной в элементе объема, к этому объему. Для однородного поля объемная плотность энергии равна  . Для плоского конденсатора, объем которого Sd, где S - площадь пластин, d - расстояние между пластинами, имеем:

С учетом, что  и :

или .

12. Носители тока в средах. Сила и плотность тока. Уравнение непрерывности. Электрическое поле в проводнике с током. Силовые линии электрического поля и линии тока.

Электрический ток — упорядоченное некомпенсированное движение свободных электрически заряженных частиц, например, под воздействием электрического поля. Такими частицами могут являться: в проводниках — электроны, в электролитах — ионы (катионы и анионы), в газах — ионы и электроны, в вакууме при определенных условиях —электроны, в полупроводниках — электроны и дырки (электронно-дырочная проводимость).

Сила тока — скалярная физическая величина, определяемая отношением заряда Δq, проходящего через поперечное сечение проводника за некоторый промежуток времени Δt, к этому промежутку времени.

Единицей силы тока в СИ является ампер (А).

Если сила тока и его направление со временем не изменяются, то ток называется постоянным.

Единица силы тока — основная единица в СИ 1 А — есть сила такого неизменяющегося тока, который, проходя по двум бесконечно длинным параллельным прямолинейным проводникам очень маленького сечения, расположенным на расстоянии 1 м друг от друга в вакууме, вызывает силу взаимодействия между ними 2·10-7 Η на каждый метр длины проводников.

Рассмотрим, как зависит сила тока от скорости упорядоченного движения свободных зарядов.

Выделим участок проводника площадью сечения S и длиной Δl (рис. 1). Заряд каждой частицы q0. В объеме проводника, ограниченном сечениями 1 и 2, содержится nSΔl частиц, где n — концентрация частиц. Их общий заряд 

Рис. 1

Если средняя скорость упорядоченного движения свободных зарядов , то за промежуток времени  все частицы, заключенные в рассматриваемом объеме, пройдут через сечение 2. Поэтому сила тока: 

Таким образом, сила тока в проводнике зависит от заряда, переносимого одной частицей, их концентрации, средней скорости направленного движения частиц и площади поперечного сечения проводника.

Заметим, что в металлах модуль вектора средней скорости упорядоченного движения электронов  при максимально допустимых значениях силы тока ~ 10-4 м/с, в то время как средняя скорость их теплового движения ~ 106 м/с.

Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника, т.е. 

В СИ единицей плотности тока является ампер на квадратный метр (А/м2).

Как следует из формулы (1), . Направление вектора плотности тока  совпадает с направлением вектора скорости упорядоченного движения  положительно заряженных частиц. Плотность постоянного тока постоянна по всему поперечному сечению проводника.

Уравнение непрерывности.

Представим себе, в некоторой проводящей среде, где течет ток, замкнутую поверхность S. Для замкнутых поверхностей векторы нормалей, а следовательно, и векторы  принято брать наружу, поэтому интеграл  дает заряд, выходящий в единицу времени наружу из объема V, охваченного поверхностью S. Мы знаем, что плотность постоянного электрического тока одинакова по всему поперечному сечению S однородного проводника. Поэтому для постоянного тока в однородном проводнике с поперечным сечением S сила тока:

(

 Из (7.3.1) и постоянства значения I во всех участках цепи постоянного тока следует, что плотности постоянного тока в различных поперечных сечениях 1 и 2 цепи обратно пропорциональны площадям  и  этих сечений (рис. 7.2):

.

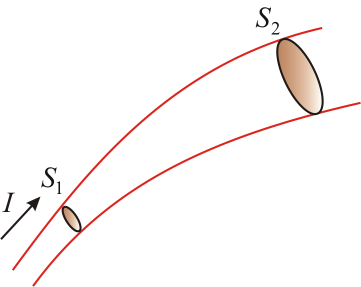
Пусть S – замкнутая поверхность, а векторы  всюду проведены по внешним нормалям . Тогда поток вектора  сквозь эту поверхность S равен электрическому току I, идущему вовне из области, ограниченный замкнутой поверхностью S. Следовательно, согласно закону сохранения электрического заряда, суммарный электрический заряд q, охватываемый поверхностью S, изменяется за время  на , тогда в интегральной форме можно записать:

.

(

  Это соотношение называется уравнением непрерывности. Оно является, по существу, выражением закона сохранения электрического заряда.

      Дифференциальная форма записи уравнения непрерывности записывается так:

или

(

  В случае постоянного тока, распределение зарядов в пространстве должно оставаться неизменным:

      следовательно,

(

это уравнение непрерывности для постоянного тока (в интегральной форме).  Линии  в этом случае нигде не начинаются и нигде не заканчиваются. Поле вектора  не имеет источника. В дифференциальной форме уравнение непрерывности для постоянного тока . Если ток постоянный, то избыточный заряд внутри однородного проводника всюду равен нулю. В самом деле, т.к. для постоянного тока справедливо уравнение , то

 Избыточный заряд может появиться только на поверхности проводника в местах соприкосновения с другими проводниками, а также там, где проводник имеет неоднородности.

Силовые линии электрического поля и линии тока.

Электрическое поле наглядно изображается с помощью силовых линий. Силовой линией электрического поля называется линия, в каждой точке которой касательная совпадает с вектором напряженности поля. Силовые линии проводятся с такой густотой, чтобы число линий, пронизывающих воображаемую площадку 1м², перпендикулярную полю, равнялось величине напряженности поля в данном месте. Тогда по изображению электрического поля можно судить не только о направлении, но и о величине напряженности поля. Электрическое поле называется однородным, если во всех его точках напряженность Е одинакова. В противном случае поле называется неоднородным.

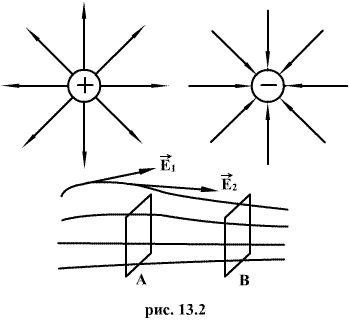
При положительном заряде, образующем поле, вектор напряженности направлен вдоль радиуса от заряда, при отрицательном - вдоль радиуса по направлению к заряду. Исходя из положительного заряда (или входя в отрицательный заряд) силовые линии теоретически простираются до бесконечности.

Линии тока векторного поля р - линии, в каждой точке которых касательная имеет направление вектора поля в этой точке (см. Векторное поле). Дифференциальные уравнения Линии тока имеют вид:

  dx/p1 = dy/p2 = dz/p3,

где p1, p2, p3 — координаты вектора поля, а х, у, z — координаты точки Линии тока.