8.Поле на границе раздела диэлектриков

В предыдущем параграфе мы предположили, что линии поля и направление вектора поляризации перпендикулярны к границе разделами тогда . В общем случае, когда линии поля не перпендикулярны к границе раздела это отношение остается справедливым лишь для нормальных составляющих вектора электрического смещения:

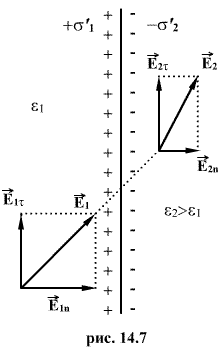
На границе двух диэлектриков с различными диэлектрическими проницаемостями , и при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов и (рис.14.7).

Дополнительное поле, создаваемое этими зарядами, перпендикулярно поверхности, поэтому нормальные составляющие полей , и в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.

(14.11)

Векторы электростатического смещения в обеих средах соответственно равны

и

(14.12)

Аналогично рассмотренному выше случаю границы диэлектрик - вакуум нормальная составляющая вектора на границе двух диэлектриков а отсюда следует, что

Из этого выражения следует, что в случае и линии вектора при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что

При и

При переходе через границу раздела из диэлектрика с меньшим значением в диэлектрик с большим значением , нормальная составляющая вектора остается неизменной, а касательная увеличивается, так что линии вектора преломляются под таким же углом как и линии напряженности поля (рис. 14.8).

Таким образом, при переходе через границу раздела двух диэлектриков изменяется не только вектор напряженности электрического поля , но и вектор . Однако поток вектора через произвольную площадку на границе раздела, равный по определению , с обеих сторон поверхности на основании остается неизменным. Следовательно, число линий вектора электрического смещения, переходящих через границу, не меняется. Поэтому теорема Гаусса остается справедливой для вектора в самом общем случае при наличии в поле диэлектриков любой формы и размеров.

9. Энергия системы неподвижных точечных зарядов.

Как мы уже знаем, электростатические силы взаимодействия консервативны; значит, система зарядов обладает потенциальной энергией. Будем искать потенциальную энергию системы двух неподвижных точечных зарядов Q₁ и Q₂, которые находятся на расстоянии r друг от друга. Каждый из этих зарядов в поле другого обладает потенциальной энергией (используем формулу потенциала уединенного заряда):    где φ₁₂ и φ₂₁ — соответственно потенциалы, которые создаются зарядом Q₂ в точке нахождения заряда Q₁ и зарядом Q₁ в точке нахождения заряда Q₂. Согласно,   и   поэтому W₁ = W₂ = W и    Добавляя к нашей системе из двух зарядов последовательно заряды Q₃, Q₄, ... , можно доказать, что в случае n неподвижных зарядов энергия взаимодействия системы точечных зарядов равна   (1)  где φ_i — потенциал, который создается в точке, где находится заряд Q_i, всеми зарядами, кроме i-го. 

Поле вблизи поверхности проводника.

  Выделим на поверхности S проводника площадку dS и построим на ней цилиндр с образующими, перпендикулярными к площадке dS, высотой dl (рис. 5.2).

      На поверхности проводника вектор напряженности поля  и вектор электрического смещения  перпендикулярны поверхности. Поэтому поток  сквозь боковую поверхность равен нулю.

      Поток вектора электрического смещения  через  тоже равен нулю, так как  лежит внутри проводника, где  и, следовательно, . Отсюда следует, что поток  сквозь замкнутую поверхность равен потоку  через :

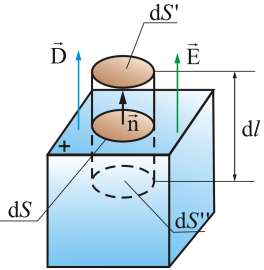
Рис. 5.2

      С другой стороны, по теореме Остроградского-Гаусса:

где σ – поверхностная плотность зарядов на dS. Из равенства правых частей следует, что , тогда

.

(5.2.1)

Итак, напряженность поля вблизи поверхности заряженного проводника прямо пропорцианальна поверхностной плотности зарядов.

Электроёмкость.

Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:

В системе СИ единица электроемкости называется фарад (Ф): 

Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники. Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, – обкладками.