3405

3.6 Определение количества теплоты, отданного цилиндром в процессе охлаждения

Так же как и для пластины, количество теплоты Qп, Дж, которое отдается или воспринимается поверхностью цилиндра за время от 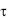= 0 до 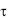= , должно равняться изменению внутренней энергии цилиндра за период полного его охлаждения:

(R изменяется от 0 до 1).

Если в это уравнение подставить значение согласно уравнению (3.53) и проинтегрировать в указанных ранее пределах, то получим:

Fo 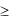0,25 также можно ограничиться одним первым членом ряда (3.65):

198

считать для соответствующих значений Bi и свести в таблицы.

3.7 Охлаждение шара

Рассмотрим охлаждение шара в среде с постоянной температурой и с постоянным коэффициентом теплоотдачи на его поверхности. В начальный момент времени при 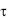= 0 все точки шара с радиусом го имеют одинаковую температуру t0. При заданных условиях температура для любой точки шара будет функцией только времени и радиуса. Требуется найти распределение температуры внутри шара.

Если обозначить избыточную температуру для любой точки шара = t . tж, то дифференциальное уравнение теплопроводности шара в сферических координатах запишется:

198

здесь = / 0; R = r/r0.

Постоянная в уравнении (3.68) является корнем харак-

Уравнение (3.69) является трансцендентным, имеет бесчисленное множество корней при заданном значении Bi и решается аналогично уравнению (3.14). Значения шести корней уравнения (3.69) для различных Bi приведены в [Л.111, табл.

6.5].

При Bi 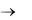согласно характеристическому уравнению

(3.69)

n n ,

при этом «начальная тепловая амплитуда» уравнения (3.68)

При Bi = 1 согласно уравнению (3.69):

При малых значениях Bi (Bi < 0,l) начальные амплитуды (Dn) всех членов ряда (3.68), за исключением первого, стремятся к нулю. Начальная амплитуда первого члена ряда D1 = 1, a 21 = 3Bi При этих условиях соотношение (3.68) запишется

198

Из анализа уравнения (3.68) следует, что при значениях Fo 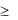0,25 ряд становится настолько быстросходящимся, что для выражения температурного поля можно ограничиться первым членом ряда:

Так как n в уравнении (3.68) зависят только от числа Bi, то уравнение температурного поля может быть записано в ви-

Функции, определяемые выражениями (3.74 ) и (3.74) для различных значений чисел Bi и Fo, представлены на рис.

3.13 и 3.14.

198

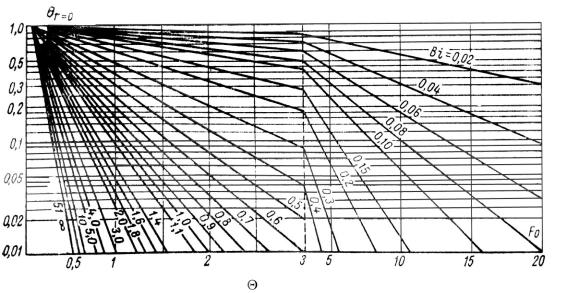
Рис. 3.13 Зависимость = F1 (Fo, Bi) для центра шара

198

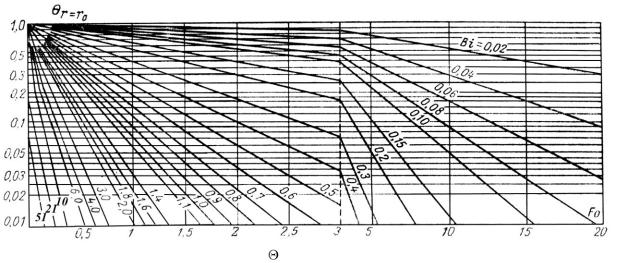
Рис. 3.14 Зависимость = F2 (Fo, Bi) для поверхности шара

198

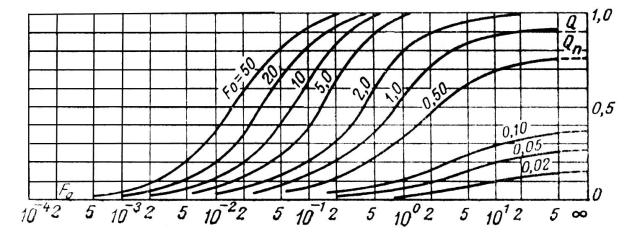
Рис. 3.15. Зависимость Q/Qп = F (Fo, Bi).

198

Аналогично, как для пластины и цилиндра, количество теплоты, которое отдается или воспринимается шаром за про-

быточная внутренняя энергия шара. Из рассмотрения (3.75) следует, что

Значения функции (3.76) для различных значений чисел Fo и Вi представлены на рис. 3.15.

3.8 Охлаждение (нагревание) тел конечных размеров

а) Охлаждение параллелепипеда

Рассмотрим охлаждение параллелепипеда в среде с постоянной температурой и с постоянным коэффициентом теплоотдачи на всех его гранях. В начальный момент времени ( = 0) все точки параллелепипеда имеют одинаковую температуру t0. Параллелепипед с размерами 2 x 2 y 2 z является однородным и изотропным. Требуется найти распределение температуры в параллелепипеде для любого момента времени, а также среднюю температуру, необходимую для определения количества подведенной (отведенной) теплоты.

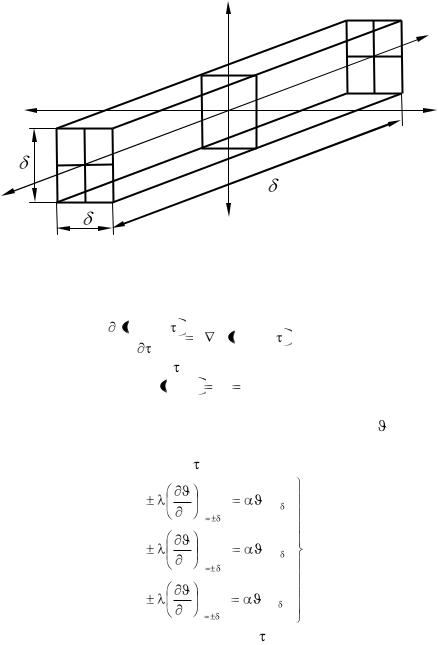
Поместим начало координат в центре параллелепипеда

(рис. 3.16).

198

Рис. 3.16 К охлаждению параллелепипеда

При этом днфференциальное равнение запишется следующим образом:

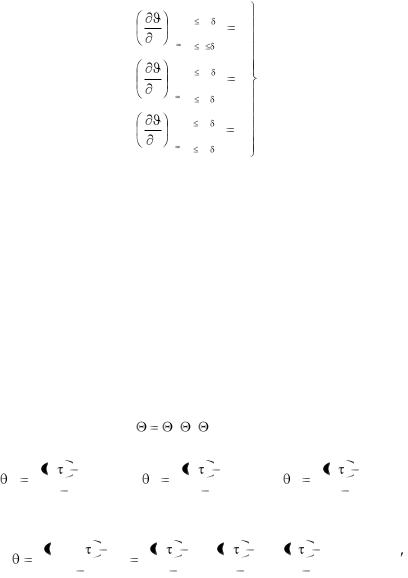
б) в центре параллелепипеда при > 0

198

Параллелепипеды, цилиндры конечных размеров и прямоугольные стержни можно рассматривать как тела, образованные пересечением соответственно трех взаимно перпендикулярных неограниченных пластин конечной толщины, цилиндра в пластины и двух пластин.

Можно доказать, что решение таких задач представляется произведением безразмерных температур для тел неограниченных размеров, в результате пересечения которых образовалось рассматриваемое тело.

Как было сказано, параллелепипед образован в результате пересечения трех взаимно перпендикулярных безграничных пластин конечной толщины. Следовательно, для него и решение можно представить, как произведение безразмерных тем-

Приведенное решение удовлетворяет как дифференциальному уравнению, так и граничным условиям, описывающим процесс теплопроводности в параллелепипеде.

Таким образом, решение задачи для рассматриваемого

198