
3405
.pdf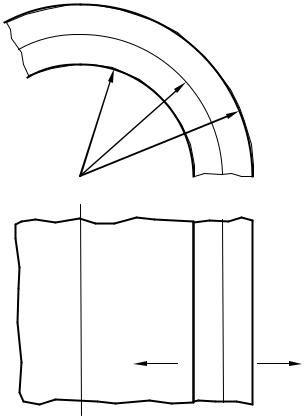
r1 |
r0 |
|
r2 |
||
|
tc1 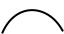 tc2
tc2
q1 |
q2 |
Рис. 2.28 Теплота внутренних источников отводится через обе поверхности цилиндрической стенки
Вслучае, когда теплота отдается окружающей среде как
свнутренней, так и с внешней поверхности, должен существовать максимум температуры внутри стенки. Изотермическая
поверхность, соответствующая максимальной температуре t0, разделяет цилиндрическую стенку на два слоя. Во внутреннем слое тепло передается внутрь трубы, во внешнем — наружу. Максимальное значение температуры соответствует условию dt/dr = 0, и следовательно, q = 0.
Таким образом, для решения данной задачи можно использовать уже полученные выше соотношения. Для этого
198
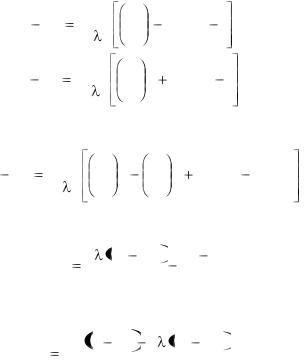
нужно знать радиус r0 (рис. 2.28), соответствующий максимальной
температуре t0.
Согласно уравнениям (2.156) и (2.162) максимальные перепады температур во внешнем и внутреннем слоях определяются уравнениями:
|
|
|
|
|
|
|
|
q |
r 2 |
|
|
r |
|
|
r |
|
|
|
|
|
|
||||||||
|
|
t |
|
t |
|
|
|
|
|
|
v 0 |
|
2 |
|
|
|
2 ln |
2 |
|
1 ; |
|
|
(а) |
||||||
|
|
0 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
4 |
|
|
|
|
r0 |
|
|
r0 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
q |
|
r 2 |
|
r |
2 |
|
|
r |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
t |
|
t |
|
|
|
|
|
v 0 |
|
|
1 |
|
|
|
2 ln |
0 |
1 . |
|
|
(б) |
|||||||
|
|
0 |
c1 |
4 |
|
|
|
r0 |
|
|
r1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Вычитая соответственно левые и правые части двух по- |
|||||||||||||||||||||||||||||
следних уравнений, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
q |
r 2 |
|
|
r |
2 |
|
|
|
r |
2 |
|
|
|
|
r |
|
r |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
t |
|
t |
|
|
|
v 0 |
|
2 |
|
|
|
|
1 |
|
|
2 ln |
0 |
|
2 ln |
0 |
. |
||||||||
c1 |
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
|
|
|
|
|
r0 |
|
|
|
|
|
r0 |
|
|
|
|
|
r2 |
|
r1 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Это уравнение необходимо решить относительно r0. Решив, получим:
r 2 |
4 |
t c1 t c2 |
||||
|
|
|
|
|
||
0 |
|
|
|
r1 |
|
|
|
q |
|
2 ln |
|
||
v |
r2 |
|||||
|
|
|
||||
|
|
|
|
|||
r 2 |
r 2 |
|
|
2 |
1 |
|
, |
2 ln |
r1 |
|
|
|
|
||
r2 |
|
||
|
|
||
или
r 2 |
q |
r 2 |
r 2 |
4 t |
c1 |
t |
c2 |
|
|
|||
|
v 2 |
1 |
|
|
|
|
|
. |
(2.163) |
|||
|
|
|
|
|
|
|
|
|
|
|||
0 |
|
|
|
|
|
r2 |
|
|
|
|
|
|
|
|
|
q |
|
2 ln |
|
|
|
|
|
|
|
|
|
|
v |
r1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||
Подставив вычисленное из уравнения (2.163) значение в выражения (а) и (б), найдем максимальную температуру в рассматриваемой стенке.
Для нахождения распределения температуры во внутреннем слое в уравнение (2.161) подставляются значения текущей координаты r1 < r < r0, а для нахождения распределения температуры во внешнем слое в уравнение (2.157) подставляются значения r0 < r < r2.
198

Если температуры внешних поверхностей цилиндрической стенки tc1 и tc2 равны, то уравнение (2.163) упрощается. В этом случае
r 2 |
r 2 |
r 2 |
|
|
|
2 |
1 |
|
, |
(2.163 ) |
|
|
|
|
|||
0 |
|
r2 |
|
|
|
|
2 ln |
|
|
|
|
|
r1 |
|
|
||
|
|
|
|
||
т. е. зависит только от размеров цилиндрической стенки и не зависит от тепловых условий. Например, при r2 = 2 и r1 = 1,
r0 = 1,46.
Если температуры поверхностей цилиндрической стенки tc1 и tc2 неизвестны, но известны температуры жидкостей tж1 и tж2 внутри и вне трубы и коэффициенты теплоотдачи 1 и 2 , то для определения r0 к уравнению (2.163) необходимо добавить уравнения
q q
l1 |
1 t c1 |
t ж1 |
2 r1 |
; |
(в) |
|
2 t c2 |
t ж 2 2 r2 , |
|||
l2 |
|
||||
где
q |
l1 |
q |
r 2 |
r 2 |
; |
q |
l2 |
q |
v |
r 2 |
r 2 . |
|
|
v 0 |
1 |
|
|
|
2 |
0 |
Для определения r0 нужно решать уравнения (в) совместно с уравнением (2.163).
3 НЕСТАЦИОНАРНЫЕ ПРОЦЕССЫ ТЕПЛОПРОВОДНОСТИ
3.1 Общие положения
Процессы теплопроводности, когда поле температуры в теле изменяется не только в пространстве, но в во времени, называют нестационарными. Они имеют место при нагревании (охлаждении) различных заготовок и изделий, производстве стекла, обжиге кирпича, вулканизации резины, пуске и остановке различных теплообменных устройств, энергетических агрегатов и т. д.
198
Среди практических задач нестационарной теплопроводности важнейшее значение имеют две группы процессов: а) тело стремится к тепловому равновесию; б) температура тела претерпевает периодические изменения.
К первой группе относятся процессы прогрева или охлаждения тел, помещенных среду с заданным тепловым состоянием, например, прогрев болванки в печи, охлаждение металлических брусков и чушек, охлаждение закаливание детали и т. п.
Ко второй группе относятся процессы в периодически действующих подогревателях, например тепловой процесс регенераторов, насадка которых то нагревается дымовыми газами, то охлаждается воздухом. На рис. 3.1 показан характер кривых, полученных при нагревании однородного твердого тела в среде с постоянной температурой tж. По мере нагрева температура в каждой точке асимптотически приближается к температуре нагревающей среды. Наиболее быстро изменяется температура точек, лежащих вблизи поверхности тела. С увеличением времени прогрева эта разность будет уменьшаться и теоретически через достаточно большой отрезок времени она будет равна нулю.
В условиях передачи теплоты через стенку при внезапном изменении температуры одного из теплоносителей не вся теплота будет передаваться через стенку; часть ее уйдет на изменение внутренней энергии самой стенки (ее температуры), и только при наступлении стационарного процесса вся теплота будет передаваться через стенку от одной жидкости к другой.
198
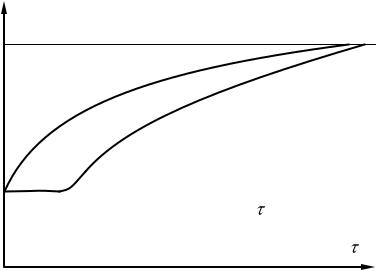
t |
tж |
|
tс
tоси
t = f ( )
0
Рис. 3.1 Характер изменения температуры тела во времени
Приведенные примеры указывают на то, что нестационарные тепловые процессы всегда связаны с изменением внутренней энергии или энтальпии вещества.
В настоящее главе будет рассмотрено лишь несколько наиболее важных задач, относящихся к процессам, в которых тело стремится к тепловому равновесию. Цель такого рассмотрения заключается в том, чтобы познакомиться с методом решения задачи нестационарной теплопроводности и получить математические соотношения для практических расчетов. Для более широкого ознакомления с решениями большого круга задач нестационарной теплопроводности как в случае стремления температуры тела к состоянию равновесия, так и ее периодического изменения следует обратиться к монографии А.В. Лыкова и другой специальной литературе.
198
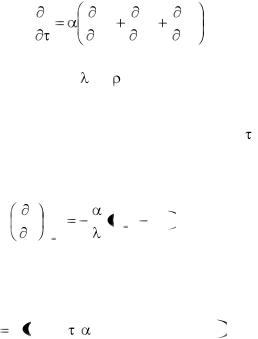
3.2 Аналитическое описание процесса
Аналитическое описание процесса теплопроводности включает в себя дифференциальное уравнение и условия однозначности.
Дифференциальное уравнение теплопроводности при отсутствии внутренних источников теплоты имеет вид:
|
t |
2 t |
|
2 t |
|
2 t |
. |
(3.1) |
|
|
|
|
x 2 |
|
y2 |
|
z 2 |
||
|
|
|
|
|
|
|
|||
Условия однозначности задаются в виде: |
|
|
|||||||
физических параметров |
, с, |
; |
|
|
|
|
|
||
формы и геометрических размеров объекта l0, l1, l2, …, ln; (3.2)
температуры тела в начальный момент времени = 0
t = t0 = f (x, y, z).
Граничные условия могут быть заданы в виде граничных условий третьего рода:
t |
|
|
t n 0 |
t ж . |
|
|
|
||
n |
|
|||
n 0 |
|
|||
Дифференциальное уравнение теплопроводности (3.1) совместно с условиями однозначности (3.2) дает законченную математическую формулировку рассматриваемой задачи. Решение ее заключается в отыскании функции
t f x, y, z, , , a, t 0 , t ж , l0 , l1 ,.., ln , |
(3.3) |
которая удовлетворяла бы уравнению (3.1) и условиям (3.2). Рассмотрим подробно решение задачи об охлаждении
плоской однородной стенки и получим для этого случая конкретный вид функции (3.3). Изучив метод решения задачи для пластины, можно понять принцип решения задач и для тел другой геометрической конфигурации.
198

3.3 Охлаждение (нагревание) неограниченной пластины
Постановка задачи. Дана пластина толщиной 2 . Если толщина пластины мала по сравнению с длиной и шириной, то такую пластину обычно считают неограниченной.
t
0
t0
t ж
x
0 2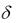
Рис. 3.2 К охлаждению плоской неограниченной пластины. При = 0 задано t0 = const и 0 = const
При заданных граничных условиях коэффициент теплоотдачи одинаков для всех точек поверхности пластины. Изменение температуры происходит только в одном направлении
х, |
в |
двух других направлениях температура не изменяется |
( |
t/ |
y = t/ z = 0) следовательно, в пространстве задача являет- |
ся одномерной. Начальное распределение температуры задано некоторой функцией t (x, 0) = f (x). Охлаждение происходит в среде с постоянной температурой tж = const. На обеих поверхностях от вод теплоты осуществляется при постоянном во
198

времени коэффициенте теплоотдачи. Отсчет температуры пластины для любого момента времени будем вести от температуры окружающей среды, т. е. t – tж = .
Так как задача в пространстве одномерная, то дифференциальное уравнение (3.1) принимает вид:
|
2 |
|
|
|||
|
|
|
a |
|
. |
(3.4) |
|
|
|
x 2 |
|||
Начальные условия: |
|
|||||
при = 0 |
= 0 = f(x) – tж = F (x). |
(3.5) |
||||
При заданных условиях охлаждения задача становится симметричной и начало координат удобно поместить на оси пластины, как показано на рис. 3.2. При этом граничные условия на оси и на поверхности пластины запишутся так:
а) аз оси пластины при x = 0 |
|
|
|
|
0 ; |
|||
|
x x 0 |
|||||||
|
|
|
|
|
|
|||
б) на поверхности пластины при x = |
|
|
||||||
|
|
|
|
|
|
x |
. |
(3.6) |
|
x |
|
|
|
|
|||
|
|
|
|
|
|
|
||
|
x |
|
|
|||||
Дифференциальное уравнение (3.4) совместно с начальными (3.5) и граничными (3.6) условиями однозначно формируют поставленную задачу. Решение дифференциального уравнения (3.4) с учетом начальных и граничных условий и дает искомое распределение температуры в плоской пластине.
Решение дифференциального уравнения (3.4) ищем в виде произведения двух функций, из которых одна является функцией только , а другая . только х (метод разделения переменных):
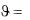
 , x
, x 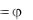
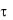 x . (3.7)
x . (3.7)
После подстановки последнего выражения в дифференциальное уравнение (3.4) получим:
|
|
|
2 |
x |
|
|
x a |
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
или |
|
|
||
198

x a x |
. |
В этом уравнении легко разделяются переменные, и его можно записать следующим образом:
a |
x |
. |
(3.8) |
|
|||
|
x |
|
|
Левая часть уравнения (3.8) есть функция только , а правая - функция только х.
Если зафиксировать аргумент х в менять только , то при любом его значении левая часть уравнения (3.8) равна постоянной величине, стоящей в правой части, т. е.  ( ) = const. Аналогично при фиксации
( ) = const. Аналогично при фиксации 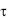 и изменении х правая часть уравнения (3.8) для любого значения х должна равняться постоянной левой части, которая зависит только от , т. е.
и изменении х правая часть уравнения (3.8) для любого значения х должна равняться постоянной левой части, которая зависит только от , т. е.  (x)/ (x) = const.
(x)/ (x) = const.
Так как равенство (3.8) должно иметь место при любых значениях х в , то обе его части должны быть равны одной в той же постоянной величине. Обозначим последнюю через 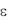 и перепишем соотношение (3.8):
и перепишем соотношение (3.8):
1 |
|
|
|
x |
const . |
|
|
|
|
|
|
a |
|
|
|
x |
|
|
|
|
|
Заметим, что нетривиальное |
решение для функции (х) |
получаем не при всех значениях , |
а только при < 0. Так как |
пока произвольная постоянная по численному значению, то
полагаем = .k2. Подставляя это значение для |
, получим: |
|||||||||
1 |
|
|
|
|
x |
|
const |
k 2 , |
|
|
|
|
|
|
|
|
|
|
|
||
|
a |
x |
|
|
||||||
|
|
|
|
|
||||||
откуда |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
ak 2 |
0 ; |
(3.9) |
|
|
|
|
|
x |
k 2 x |
0 . |
(3.10) |
|||
Постоянная k определяется из граничных условий, а знак минус выбирается из физических соображений. Для тепловых процессов, стремящихся к тепловому равновесию, знак может быть только минус.
198

В результате мы получили систему обыкновенных дифференциальных уравнений (3.9) и (3.10), которые легко интегрируются.
Уравнению (3.9) удовлетворяет функция |
C1e ak 2 . |
Уравнению (3.10) удовлетворяет функция вида: |
|
x C 2 sin kx C3 cos kx . |
|
Подставляя полученные выражения для ( ) |
и (x) в |
уравнение (3.7), получаем частное решение: |
|
C |
2 |
sin kx C |
3 |
cos kx C e ak 2 . |
(3.11) |
|
|
1 |
|
||
Выражение (3.11) |
удовлетворяет исходному уравнению |
||||
(3.4) при любых значениях постоянных C1, C2, C3 и k.
Для того чтобы уравнение (3.11) было решением поставленной задачи, его нужно подчинить начальным и граничным условиям. Подчиняя уравнение (3.11) граничным условиям при х = 0
|
|
|
|
|
0 . |
|
|
|
|
|
x |
|
|||
|
|
|
x 0 |
|
|||
находим: |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
C1e ak 2 k C2 cos kx C3 sin kx |
|
0 , |
|||
|
x |
||||||
|
x 0 |
|
x |
0 |
|||
или |
|
|
|
|
|
|
|
|
|
C2 cos 0 |
C3 sin 0 , |
|
|||
Это значит, что частное решение x C2 sin kx долж-
но быть отброшено как не удовлетворяющее заданным граничным условиям.
Если учесть, что С2 = 0, и обозначить С2С3 = А, то уравнение (3.11) можно записать в виде
Ae ak 2 cos kx . |
(3.12) |
Подчинив частное решение (3.12) граничному условию
|
|
|
x |
, |
x |
|
|
||
|
|
|
||
x |
|
|||
получим:
198
