3188

воспринимаемого датчиками. Ввиду этого устройство способно определять, находится ли высота объекта в пределах данного интервала.

Чтобы уменьшить число «призраков», возникающих благодаря затенению ленты конвейера частью объекта, еще не достигшей прямой, на которую сфокусирована фотолинейка, добавлены еще два источника света (однако проблему представляют глубокие отверстия, которые не будут обнаруживаться устройством).

На этом рисунке, например, поверхность освещается полоской света. Фотолинейка расположена вертикально над прямой, по которой полоса пересекает поверхность ленты конвейера. Когда на ней находится объект, то он загораживает свет и тот не достигает поверхности. Фотолинейка воспримет свет только в том случае, когда он достигнет поверхности. Чтобы получить полное изображение, необходимо пропустить весь объект через светочувствительную область воспринимающего устройства.

1.3.7. Пространственная взаимосвязь

На типичных изображениях уровни яркости соседних элементов не являются независимыми. Например, можно заранее предсказать, что изображение многогранного объекта содержит области с практически постоянной яркостью. Аналогично яркость изображений объектов с гладкой поверхностью изменяется постепенно. Мы воспользуемся такой пространственной взаимосвязью несколькими способами.

При сегментации изображения обязательно найдется несколько неправильно классифицированных элементов (в основном благодаря шуму). Если отношение сигнал — шум мало, почти все эти ошибки будут изолированы, за исключением элементов, расположенных вблизи границы объекта. Такой эффект называется крапчатым шумом. После разделения по порогу подобные ошибки нетрудно устранить, если учесть, что соседние элементы будут иметь противоположное значение.

Однако можно попытаться на первом же этапе избежать

158

возникновения такого сорта ошибок путем исследования уровней яркости соседних элементов до порогового разделения. Если уровень яркости какого-то элемента изображения выше максимального уровня его соседей, то, вероятно, он б(ыл подвержен воздействию шума. Это — «выброс». Его необходимо заменить максимальным уровнем яркости

соседних элементов. Аналогичную «фильтрующую» операцию можно применить, если уровень яркости элемента ниже минимального уровня его соседей. Заметьте, что после такой операции полутона элементов изображения, находящихся на границе между объектом и фоном, останутся без изменения.

Снижения шума можно достигнуть и с помощью других фильтрующих операций. Мы уже упоминали операцию усреднения по значениям соседних элементов. Она приводит к сглаживанию особенностей и потому уменьшает пространственное разрешение. В результате усложняются проблемы, встречающиеся на границах. Другая возможность заключается в замене каждого значения уровня не средним, а медианным значением соседних элементов. (Числа элементов множества, лежащих ниже и выше медианы, равны.)

Как и в первой схеме, такая операция не изменяет значений элементов на границе. Однако вычислить медиану сложнее, чем максимальное или среднее значение.

Каждый из описанных методов позволяет уменьшить количество элементов изображения, которые в дальнейшем будут неправильно классифицированы в процессе бинаризации. Однако они не гарантируют получения абсолютно надежных результатов. Случайный шум может привести к появлению неожиданного уровня яркости не только в отдельном, но и в нескольких соседних элементах. При этом малая вероятность возникновения значительной ошибки в одном элементе умножается на малые вероятности значительных ошибок в соседних. Поэтому вероятность того, что среднее значение или медиана содержат ошибку, сравнимую с ошибкой отдельного элемента, относительно

мала.

Здесь мы пользуемся пространственной взаимосвязью между элементами. В тех простых случаях, к которым мы обращались до сих пор, предполагалось, что яркость объекта приблизительно одинакова, в результате чего соседние элементы имеют близкие по

значению уровни. В таких условиях вводятся ограничения, вытекающие из предположения о том, что именно представлено на изображении. В дальнейшем мы вновь вернемся к этому подходу.

1.3.8. Сегментация изображений

Изображение желательно разбить на областих[34,35,36,37], каждая из которых соответствовала бы поверхности отдельного объекта наблюдаемой сцены. Последующую обработку можно осуществить независимо над каждой областью изображения. До сих пор мы рассматривали весьма простой случай, когда объекты и фон обладают равномерной яркостью. Теперь мы распространим эти методы на случаи, в которых каждый объект имеет яркость, отличную от яркостей других объектов.

Если нам известен средний уровень яркости каждого объекта, то нетрудно выбрать пороговые значения, заключенные между этими уровнями, что позволит нам классифицировать любой элемент изображения. Однако сразу же возникают новые проблемы. Предположим, что область А примыкает к области С. Как было

которой лежит между уровнями яркости областей А к С, то часть точек границы будет классифицирована неправильно, как

Например, интересующие нас точки скорее всего образуют не широкую область в виде пятна, а изрезанную полосу с зазубренными краями. Если мы предположим, что все области обладают некоторой минимальной шириной, то нетрудно заменить ошибочно присвоенные метки. Можно также использовать тот факт, что эти неверно классифицированные точки примыкают к обеим областям и А, и С.

Иногда требуемые пороговые уровни определяют путем анализа гистограммы. Однако часто гистограмма оказывается

слишком изрезанной, поскольку лишь незначительное число точек непосредственно образуют каждый отдельный всплеск и, кроме того, эти всплески перекрываются значительно сильнее, чем в случае одного объекта и однородного фона.

Упоминавшиеся ранее проблемы шума здесь еще более серьезны. Если имеется несколько областей, то минимальная разница между их уровнями не может быть очень большой. Она должна быть малой по отношению к общему диапазону изменения уровней. Если N — общий диапазон, a R — число областей, то минимальная разность уровней должна быть меньшей или равной N/(R — 1). В итоге вероятность неправильной классификации заметно возрастает. Данную проблему можно несколько смягчить, если учесть пространственную взаимосвязь объектов.

1.3.9.Использование цвета

Другой способ улучшить классификацию состоит в использовании информации о цвете. Если даже в результате измерений с помощью единственного оптического устройства окажется, что поверхности имеют одинаковую яркость, они все же могут отличаться по цвету. Один из путей использования этого обстоятельства состоит в квантовании (по уровням яркости) нескольких изображений, полученных с помощью датчиков с различными функциями спектральной чувствительности. Этого можно достичь размещением перед объективом цветных светофильтров. Как Обычно формируются три подобных изображения (через красный, зеленый и синий фильтры). Здесь детальное поведение кривых спектральной чувствительности этих фильтров значения не имеет.

Уровни яркости трех зарегистрированных изображений удобно объединить в один вектор, приписываемый соответствующему пикселу. Каждая компонента вектора представляет собой уровень яркости изображения в этом пикселе, полученный с помощью одного из фильтров. Отдельной области отвечает одна или множество точек в соответствующем векторном пространстве.

Разбить цветовое пространство на части, отвечающие различным областям, не просто. При обсуждении темы, относящейся к классификации образов, мы отметим некоторые методы, позволяющие осуществить это. Один из них состоит в измерении расстояния от представительного или среднего вектора, отнесенного к каждой области. Неизвестный вектор можно затем приписать тому классу, который соответствует ближайшему вектору

—представителю. Это равнозначно разбиению пространства плоскостями, которые перпендикулярны отрезкам между векторами

—представителями и делят эти отрезки пополам.

1.3.10.Наращивание и разбиение областей

Допустим, что тем или иным методом мы произвели детальную, но грубую сегментацию изображения. Например, просто объединили в группы соседние элементы с одинаковыми уровнями яркости. Дальнейшее улучшение сегментации достигается слиянием соседних областей с близкими уровнями. «Близость» может означать, что уровни отличаются меньше некоторой пороговой величины. При проверке на близость могут также учитываться геометрические факторы, например отношение длины общей границы к суммарной длине границ двух областей.

Более сложная проверка основана на оценке среднего уровня яркости и его вариаций внутри каждой области. С помощью стандартных методов, заимствованных из статистики, нетрудно определить, какова вероятность того, что разные области случайно имеют близкие уровни -яркости. Если вероятность мала, то мы объединяем такие области. Слияние — это монотонная операция, которая обязательно завершится. Конечно, при этом возможен и такой исход, что все изображение будет отождествлено с одной областью!

Иногда подобный процесс слияния приводит к объединению областей с близкими уровнями, которые объединять не следовало бы. Ошибки такого рода можно выявить по геометрическим соображениям. Например, если на границе имеются два ярко выраженных выреза, идущих приблизительно с противоположных

162

сторон, то весьма вероятно, что разграничительную линию необходимо провести между их концами. Оценка среднего и разброса значений полутонов для выделенных областей может подтвердить правильность этого предположения. Подобные методы применяются в основном для разбиения, а не наращивания областей. В частности, их можно использовать для выделения границ между областями с различными уровнями яркости. Более детально проблема обнаружения границ будет рассмотрена позже.

Одна из проблем, связанных с рассмотренными методами сегментации, состоит в том, что те предположения, на которых они основываются, в реальных случаях часто не соблюдаются. Хотя отражательная способность многих поверхностей и в самом деле одинакова, их изображения совершенно не обязаны сохранять это свойство. Как мы увидим позднее, на яркость изображения влияют многие факторы. Поэтому элементы изображения, отвечающие точкам поверхности различных объектов, могут иметь одинаковые уровни яркости. Только в особых случаях может оказаться целесообразным представление об изображении как о совокупности однородных по яркости областей.

Часто гораздо плодотворнее отложить сегментацию до тех пор, пока не станет известна дополнительная информация, например приблизительная форма поверхности объекта. Одна из трудностей, возникшая при построении оценочных схем для сегментации изображения, заключается в отсутствии четкой постановки самой задачи. Что такое «правильная» сегментация? Ответ на этот вопрос зависит от того, каким образом вы предполагаете использовать результат.

2.2.Обработка непрерывных изображений

Часто удобно каким-либо образом преобразовать изображение в такое, которое легче поддается дальнейшему манипулированию. Обработка изображений включает в себя поиск методов, позволяющих осуществить подобные преобразования. Большинство

163

рассмотренных до сих пор методов являются линейными: инвариантными по отношению к сдвигу, т. е. пространственноинвариантными. Методы, обладающие такими свойствами, позволяют применить мощный аналитический аппарат. В этой главе мы покажем, что линейные пространственно-инвариантные системы можно характеризовать сверткой, т. е. операцией, одномерный случай которой был введен нами при рассмотрении плотности распределения вероятности двух случайных величин.

Мы также продемонстрируем пользу[39,40,41] от введения понятия пространственной частоты и преобразований между пространственными и частотными областями. Как оптические, так и цифровые системы обработки изображений можно охарактеризовать в пространственной области функцией рассеяния точки (импульсной переходной функцией), а в частотной области — передаточной функцией. Обсуждаемые в этой главе математические приемы будут применены к анализу дифференциальных операторов, используемых при выделении краев объектов, а также методов оптимальной фильтрации, используемых при подавлении шума.

Большинство обсуждаемых здесь методов представляет собой обобщение на случай двумерных линейных систем соответствующего аппарата, относящегося к одномерным сигналам, однако мы не будем предполагать знакомство читателя с этим аппаратом. В настоящей главе рассматривается непрерывный, а в следующей главе — дискретный случаи.

2.2.1. Линейные пространственно-инвариантные системы

Рис. 2.2. Расфокусированное изображение g (x, у), рассматриваемое как идеальное изображение f(x, у), подвергнутое преобразованию.

Изображение можно рассматривать как двумерный сигнал. Основываясь на такой точке зрения, можно разработать соответствующий подход к обработке изображений. Рассмотрим расфокусированную зрительную систему (рис. 2.2). Изображение д(х, у), полученное с помощью такой системы, можно считать преобразованным вариантом идеального изображения f(x, у), которое было бы получено с помощью правильно сфокусированной системы. Если освещение изменится так, что яркость идеального изображения удвоится, то яркость расфокусированного изображения также удвоится. Далее, если несколько сместить зрительную систему так, что идеальное изображение слегка сместится в плоскости изображения, то расфокусированное изображение сместится подобным же образом. Поэтому говорят, что переход от идеального изображения к расфокусированному является линейной пространственно-инвариантной операцией. В действительности и более сложные оптические зрительные системы, как правило, также линейны и пространственно-инвариантны. Теперь эти понятия будут определены точнее.

Рассмотрим двумерную систему, которая при входных

сигналах f2 (х, у) и f2 (х, у) дает выходные сигналы f2 (х, у) и f2 (х, у) соответственно :

систем ограничены по величине отклика и потому не могут быть строго линейными. Более того, яркость (световая энергия, отнесенная к единице площади) не может быть отрицательной. Поэтому входной сигнал (изображение) ограничен неотрицательными значениями, хотя значения промежуточных результатов наших вычислений могут быть произвольными.

Теперь рассмотрим систему, которая по заданному входу

дает на выходе g (х, у). Система называется

пространственно-инвариантной, если для произвольных а и b

реакция системы на смещенный входной сигнал f(x — a,y — b) представляет собой смещенный выходной сигнал g(х - а,у - b).

На практике изображения ограничены по площади, так что пространственная инвариантность справедлива только для ограниченных сдвигов. Кроме того, аберрации в оптических зрительных системах зависят от расстояния до оптической оси; следовательно, такие системы лишь приблизительно пространственно-инвариантны.

Методы анализа линейных пространственно-инвариантных систем играют важную роль для понимания свойств систем формирования изображений. Недостатки последних часто можно рассматривать как результат наличия линейной пространственноинвариантной системы, которая преобразует идеальное изображение в реально наблюдаемое. Для нас более важно изучение линейных пространственно-инвариантных систем, которое приводит к полезным для обработки изображений алгоритмам, основанным либо на оптических, либо на численных методах.

Простым примером линейной пространственно-инвариантной

166

системы служит система, которая выдает производную входного сигнала по х или у. Линейность такой системы вытекает из правил дифференцирования произведения произвольной функции на постоянную величину и суммы двух функций. Также легко доказать и пространственную инвариантность. Алгоритмы вычисления производных находят применение на этапе предварительной обработки в системах выделения краев.

Мы начинаем с изучения непрерывных изображений, чтобы заложить фундамент для построения дискретных операторов. Линейные пространственно-инвариантные системы обработки изображений являются обобщением на случай двух измерений одномерных линейных

пространственно-инвариантных систем, например простых пассивных электрических цепей. Неудивительно поэтому, что подавляющую часть представленных здесь результатов можно получить путем простого обобщения способов доказательства аналогичных утверждений, относящихся к одномерному случаю. Для простоты (где это возможно) мы будем представлять функции двух переменных в виде произведения двух функций от одной переменной. Это позволит двумерные интегралы разложить на произведение двух одномерных интегралов.

При анализе одномерных систем в качестве входных и выходных сигналов обычно фигурируют временные функции. Выходной сигнал такой системы никогда не может опережать входной сигнал. Это накладывает жесткое ограничение на системы обработки одномерных сигналов: они должны быть каузальными. Физически реализуемы только те системы, которые удовлетворяют этому условию. При синтезе двумерных систем подобной проблемы не возникает.

Поскольку мы привлекаем мощные методы обработки сигналов в одномерных системах, необходимо отметить и недостатки такого подхода. Условия линейности и пространственной инвариантности являются весьма жесткими и значительно сужают наши возможности работы с изображением. Все же трудно добиться какого-либо прогресса без руководящей теории.

167

2.2.2. Cвертка и функция рассеяния точки

Рассмотрим систему, реакция которой на заданный входной сигнал[44,45]

f(х, у) имеет вид:

При этом говорят, что g — свертка функций f и h. Легко показать, что такая система линейна, поскольку ее реакция на сигнал

g1 (x, y) g2 (x, y) . Здесь, как и ранее, g1 (х, у) — реакция на сигнал fi(x,y), а g2(х,у) — на сигнал f2(х,у). Результат вытекает из

правил интегрирования произведения функции на постоянную величину и суммы двух функций. Также нетрудно убедиться в пространственной инвариантности системы: если на вход подать сигнал f(х — а, у — b), то на выходе получим g(х — а, у — b). Таким образом, система, реакцию которой можно описать операцией свертки, является линейной и пространственно-инвариантной. Скоро мы покажем и обратное, что любая линейная пространст- венно-инвариантная система описывается некоторой операцией

Было бы желательно связать функцию h (х, у) с некоторым наблюдаемым свойством системы. Всегда ли можно для произвольной функции h(x, у) найти входной сигнал f(x, у), который приводил бы на выходе к функции h(х, у)? Более точно, всегда ли можно найти функцию f(x, у), такую, что

h(x, y) f (x , y )h( , )d d ?

Беглый анализ подсказывает, что если это соотношение справедливо для произвольной функции h(x, у), то необходимо, чтобы функция f(х, у) равнялась нулю во всех точках, кроме начала координат и «бесконечности» в начале координат. «Функция», о которой идет речь, называется единичным импульсом или дельта-

по любой области, включающей начало координат, равен единице. (Если функцию двух переменных х и у рассматривать как поверхность, то этот интеграл равен объему, ограниченному этой

поверхностью.) Импульс 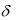не является функцией в классическом смысле (т. е. не определяется своими значениями для каждой пары аргументов). Это — обобщенная функция, которую

можно рассматривать как «предел» при 0 последовательности

квадратных импульсов размером 2по осям х и у и высотой 1/ 4 2 . Об этом подробнее будет сказано позже, а сейчас мы лишь укажем на фильтрующее свойство

(x, y)h(x, y)dxdy h(0,0)

на основе которого можно определить импульс. Из. этого

в чем можно убедиться простой заменой переменных. Сравнивая с нашим исходным уравнением для выхода системы, убеждаемся, что h (х, у) — реакция системы на вход, представленный единичным импульсом.

Рассматриваемая в виде изображения функция представляет собой черный фон везде, кроме начала координат. Поэтому функция h (х, у) говорит нам о том, как система смазывает или рассеивает светящуюся точку. В двумерном случае ее называют

функцией рассеяния точки (или импульсной переходной функцией).

Она является реакцией системы на единичный импульс и, следовательно, аналогична хорошо знакомой реакции на единичный импульс одномерной системы.

Теперь нам нужно показать, что выход любой линейной пространственно-инвариантной системы образуется путем свертки входного сигнала. Функцию рассеяния точки можно определить,

подав на вход контрольный сигнал (x, y) . Считая реакцию на единичный импульс известной, входной сигнал f(х, у) удобно представить в виде бесконечного числа смещенных

отмасштабированных единичных импульсов k( , ) (x , y ) . Простое геометрическое построение поможет представить, как это можно осуществить. Разобьем плоскость ху на квадраты со стороной

. Над каждым таким элементарным квадратом построим импульс высотой, равной среднему значению функции f(x, у) в этом квадрате. Функция f(х, у) аппроксимируется кусочно-постоянной функцией, которая представляет собой сумму всех таких импульсов.

Можно сделать еще один шаг и заменить каждый прямоугольный импульс точечным импульсом, расположенным в центре элементарного квадрата. Объем пространства под импульсом можно приравнять объему прямоугольного импульса, т. е. интегралу от функции f(х, у) по элементарному квадрату. Если функция f(х, у) непрерывна, а величина е достаточно мала, то этот интеграл можно приближенно представить в виде произведения значения f(х, у) в центре квадрата на его площадь. Требуемый результат достигается в

Точно такое же разложение функции f(х, у) на совокупность импульсов можно получить, если принять во внимание фильтрующее свойство единичного импульса. В любом случае мы приходим к выражению

170

Имея разложение функции на совокупность импульсов, можно определить суммарный выход g(х,у) на заданный вход f(х, у) путем сложения реакций системы на смещенные отмасштабированные импульсы. Это следует из линейности рассматриваемой системы.

Реакцией на импульс k (x , y ) является произведение kh(x , y ) , поскольку система пространственно-инвариантна.

Линейную пространственно-инвариантную систему всегда можно описать подходящей функцией рассеяния точки h(x, у). С помощью этой функции мы можем вычислить реакцию g (х, у) на любой заданный входной сигнал f(х, у). Функция рассеяния точки является исчерпывающей характеристикой линейной пространственно-инвариантной системы. Таким образом, мы показали, что линейная пространственно-инвариантная система осуществляет операцию свертки.

(a b) c a (b c) . Это позволяет нам рассматривать последовательность (каскад) двух систем с функциями рассеяния точки h1(x,y) и h2(x,y). Если f(х, у) — входной сигнал, то на выходе

совпадает с выходом, который мы имеем у системы с функцией рассеяния точки (h1 h2 )

2.2.3. Передаточная функция

Свертку представить гораздо труднее, чем результат произведения двух функций. Поскольку при переходе от

172

пространственной к частотной области свертка преобразуется в произведение, то в случае линейных пространственно-инвариантных систем переход к частотной области выглядит привлекательным. Однако, прежде чем развивать эти идеи, мы должны понять, что такое частота применительно к двумерным системам.

Вслучае одномерных линейных пространственно-

системы называется функция, которая воспроизводится системой, возможно, с изменением амплитуды:

Рис. 2.3. Комплекснозначные экспоненциальные собственные функции двумерной линейной пространственно-инвариантной системы.

Здесь А(w) представляет собой (возможно, комплексный) множитель, на который умножается входной сигнал. Таким образом, если на вход линейной пространственно-инвариантной системы подать сигнал в виде экспоненциальной комплекснозначной функции, то на выходе получим аналогичный по форме сигнал, умноженный на некоторый коэффициент и сдвинутый по фазе. Величина w называется частотой собственной функции. На практике

173

употребляются действительные синусоидальные сигналы, например coswt и sinwt, соответствующие действительной и мнимой частям

форма записи используется при выводе результатов, так как при этом выражения принимают более компактный вид и отпадает необходимость рассматривать косинусы и синусы отдельно.

В двумерной линейной пространственно-инвариантной

Подынтегральное выражение в правой части зависит лишь от и и v,следовательно, выходной сигнал g(х, у) — это просто умноженный на некоторый масштабный множитель и, возможно, сдвинутый по фазе входной сигнал f(x, у). Таким образом,

g(x, y) e i (ux vy ) собственная функция свертки в двумерной системе. Заметьте, что теперь частота содержит две компоненты u и v. О плоскости uv мы будем говорить как о частотной области в противоположность плоскости ху, которая представляет собой пространственную область.

Волнам в пространстве двух измерений соответствуют действительные синусоидальные гармоники cos(ux vy ) и sin(ux vy) . Максимумы и минимумы функции cos(ux vy ) лежат на параллельных

174

равноудаленных гребнях вдоль прямых ux y k , где k — целое число (рис. 2.3). Если провести сечение рассматриваемой поверхности под прямым углом к этим прямым, т. е. в направлении (u, v), то получим синусоидальные гармоники с длиной волны

2 . В чистом виде подобные гармоники в зрительной системе возникнуть не могут, поскольку яркость не бывает отрицательной. Обязательно произойдет смещение на некоторую постоянную величину. Если

рассматриваемом до сих пор, будем иметь g(х, у) = Н(u, v)f(x, у), — это видно из приведенного ранее интеграла. Таким образом, функция Н(u, v) характеризует реакцию системы на синусоидальные сигналы, точно так же как функция h (x, у) — на импульсные сигналы. Для каждого значения частоты эта функция позволяет определить амплитуду и фазу реакции системы. В случае двумерной системы ее называют передаточной функцией. Она представляет собой частотную реакцию двумерной системы на гармонический сигнал и, следовательно, аналогична известной частотной реакции одномерной системы на гармонический сигнал. (Следует иметь в виду, что функция Н(u, v) не обязана быть действительной.)

Точно так же, как о качестве звукового усилителя можно судить по его частотной характеристике, о качестве линз камеры можно, например, судить, сопоставляя графики их передаточных функций.

2.2.4. Преобразование фурье и фильтрация

Входной сигнал f(x, у) можно рассматривать как сумму бесконечного числа синусоидальных гармоник[45,46,47] (как ранее мы представили его в виде суммы бесконечного числа импульсов). Это является еще одним удобным способом разложения входного сигнала, поскольку при заданной передаточной функции Н(и, v) нам известна реакция системы на каждую компоненту разложения. Если

175

функцию f(x, у) представить в виде:

формулой, приводимой ниже.) Единственная проблема состоит в том, что разложение на гармонические сигналы совсем не так тривиально, как разложение на импульсы. Как найти функцию F(u, v), если дана f(х, у) ? Как будет показано позже, ответ будет следующим:

если этот интеграл существует. В справедливости приведенного соотношения можно убедиться, произведя замену переменных

и подставив выражение для f(х, у):

Внутренний интеграл не сходится. С помощью так называемых множителей сходимости мы позже покажем, что его

176

Функция F(u, v) называется преобразованием Фурье функции f(х, у).. Подобным же образом мы можем определить преобразование Фурье G (и, v) для выходного сигнала g(х, у). Так что окончательно G (и, v) = H(и, v)F(u, v), что проще, чем выражение

преобразованиях Фурье. Постоянные множители здесь разделены так, чтобы соответствовать принятой в других книгах форме записи. То, что преобразования почти симметричны, позволяет свойства, применимые к прямому преобразованию, переносить на обратное преобразование. Однако необходимо иметь в виду, что в общем случае F(u,v)-комплексная функция, тогда как f(x, у) - действительная. Заметьте также, что Н(u, v) - преобразование Фурье функции h(x, у).

Не для всех функций можно найти преобразование Фурье. Функции из некоторых простых классов равны интегралам Фурье от их преобразований Фурье. Однако трудно точно описать, какие функции допускают преобразование Фурье, а какие — нет.

Другого типа трудность связана с тем, что интегралы берутся по всей плоскости ху, тогда как зрительные устройства дают практически пригодные изображения только на ограниченной части плоскости изображения. Более того, в компьютерах используется только дискретное по пространству представление этих изображений. Более детально эти два вопроса будут рассмотрены в

177