3188

Вывод легко распространяется на движение в произвольном направлении. И вновь нижние частоты почти не затрагиваются, тогда как высокие гасятся. Сигналы на некоторых частотах

инвертируются, а те, для которых ul k , где k — целое число, полностью подавляются. Те сигналы, у которых гребень волны параллелен направлению движения, естественно, остаются без изменения.

2.2.11. Восстановление и улучшение изображений

Чтобы устранить эффекты размывания изображение мы можем пропустить его через систему с передаточной функцией

H '(u, ) , которая является обратной к передаточной функции

H(u, ) системы, вызывающей размывание, т. е. Н(u, v)H' (u, v) = 1. Другими словами, нам нужна система с такой импульсной функцией h' (х, у), свертка которой с функцией h (х, у) дает единичный импульс, т. е. h'(x, y) h(x, y) (x, y)

Каскад двух таких систем есть тождественная система.

Сразу возникает проблема, вызванная тем, что мы не можем восстановить частоты, которые были полностью подавлены и для которых Н (u, v) = 0. Другая проблема возникает при попытке вычисления обратного преобразования Фурье функции H' (u, v), чтобы получить функцию h' (x, у). Как правило, требуемый интеграл

не будет сходиться, хотя мы и могли бы получить результат введением множителя сходимости. Однако при этом результат не будет функцией в классическом понимании.

Самой серьезной проблемой является шум. Измерения реального изображения неточны, и возникающие погрешности мы можем, как правило, смоделировать аддитивным шумом. Шум в одной точке изображения обычно не зависит и, следовательно, не коррелирует с шумом во всех других точках. Как можно показать, отсюда следует, что шум имеет плоский спектр: энергия шума, соответствующая любому

заданному участку частотной области, имеет то же значение, что и для любого другого участка той же площади.

К сожалению, шум, о котором здесь идет речь, возникает после размывания. В результате сильно подавляемые частоты начинают смешиваться с шумом, и когда мы их пытаемся восстановить путем усиления, то усиливаем и шум. Это основная трудность, возникающая при восстановлении изображения, и ее причина состоит в том, что независимо от частоты мы не можем отличить полезный сигнал от шума.

Приведем один эвристический подход к восстановлению изображений. Мы можем создать систему, передаточная функция которой приближенно совпадает с обратной величиной передаточной функции системы, вызывающей размывание. Однако

коэффициент усиления. Можно придумать и нечто более оригинальное вроде функции H '(u, ) H (u, ) /[H (u, )2 B 2 ] ,

где 1/ 2B — максимальный коэффициент усиления при условии, что функция H (u, v) действительна (рис. 2.9).

199

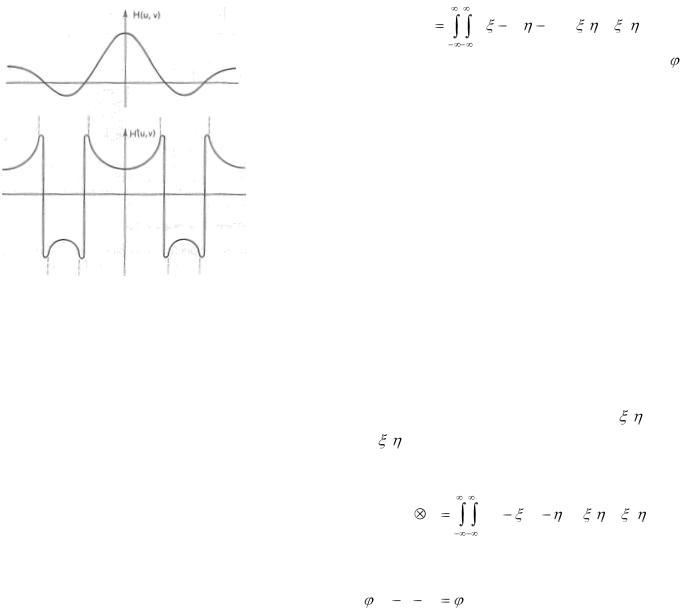
Рис. 2.9. Восстанавливающая система с передаточной функцией Н'(u, v), которая устраняет искажения, возникающие на выходе исходной системы с передаточной функцией Н(u, v). Функция Н' (u, v) обратно пропорциональна Н(u, v). На практике для ограничения усиления шума в восстанавливающей системе вводят верхний предел коэффициента усиления.

2.2.12. Корреляция и энергетический спектр

При обработке изображений иногда бывает полезно сопоставлять (коррелировать) их друг с другом. Таким путем мы, например, можем сказать, насколько похожи две яркостные картинки (рис. 2.10). Взаимная корреляция функций а (х, у) и b (x, у) определяется в виде

200

внимание, что это определение похоже на определение свертки. Единственное

В в

Рис. 2.10. Возможность использования корреляции при сравнении двух похожих изображений а(х, у) и b(х, у). Ее можно также использовать при определении положения фрагмента изображения, содержащего известный образ.

отличие заключается в аргументах первой функции подынтегрального выражения. Здесь a( , ) перед умножением на

b( , ) просто сдвигается. Кроме того, в свертке аргументы первой функции меняют знак:

Если b(х, у) = а(х, у), то результат называется автокорреляцией. Автокорреляция функции симметрична, т.е.

любой функции имеет максимум при (х, у) = (0, 0), так что для всех

сдвигом, т. е. b(х, у) = а (х - х0, у — у0), то аналогичный максимум возникает в точке, соответствующей величине сдвига, а именно

ab (x, y) для всех (х, у). Заметьте, что возможны и другие максимумы, особенно если функция а(х, у) периодическая. Тем не менее если b (х, у) мало отличается от сдвинутой функции а (х, у), то величину сдвига можно оценить путем нахождения

максимума ab .

Часто информативными оказываются преобразования Фурье взаимных корреляций и автокорреляций. По причинам, которые сейчас станут ясны, их называют энергетическими спектрами и обозначают через ФаЬ(и, v) и Фаа(и, v) соответственно. Если

преобразованием Фурье функции а (х, у) является функция А (и, v),

то Фаа (и, v) = /A(u, v)/2 =А* (и, v) А (и, v), где А * (и, v) - комплексно-

сопряженная к А (и, v) функция. Отсюда видно, что функция Фаа всегда действительна [свойство, которое можно также вывести из

симметрии aa и того факта, что преобразование Фурье функции а(- х, -у) есть А*(и, v)]. В любом случае для малых 8и и 8v величина Фаа (и, v) 8u8v представляет собой энергию, заключенную в прямоугольной области частотного диапазона, ограниченной значениями и, и + 8и и v, v + 8v. Этим и объясняется происхождение термина энергетический спектр.

Даже если интеграл Фурье для функции а(х, у) не сходится, ее энергетический спектр может существовать. Необходимо также отметить, что по А (и, v) посредством обратного преобразования Фурье функция а (х, у) восстанавливается однозначно, в то время как подобная функция, соответствующая заданному спектру Фаа(и, v), не единственна. Бесконечно много функций обладают одной и той же автокорреляцией и, следовательно, одним и тем же энергетическим спектром. Он не меняется, например, при сдвиге изображения, поскольку при этом изменяется лишь фаза в преобразовании Фурье. Если объект можно распознать по энергетическому спектру изображения, то его можно распознать независимо от его положения на изображении. В связи с этим одно время возлагали большую надежду на то, что методы Фурье-

202

преобразований сыграют значительную роль в решении задач распознавания. К сожалению, такие методы оказываются пригодными лишь тогда, когда на изображении имеется только один объект и при этом он не поворачивается и не меняется в размерах. Более того, как мы видели, энергетический спектр различных объектов может быть одинаковым. Случайный шум предоставляет другую интересную иллюстрацию. Фурье-преобразование изображения, на котором каждая точка подвержена случайному шуму с нулевым средним и стандартным отклонением а, представляет собой подобное же зашумленное изображение со

средним шума, равным нулю, и стандартным отклонением 2 . Среднее значение энергетического спектра бесконечного числа таких зашумленных изображений стремится на всех частотах к

постоянному значению. ( 2 )2.

2.2.13. Оптимальная фильтрация и подавления шума

Данный раздел, относящийся к оптимальной фильтрации, требует некоторого терпения при прослеживании нетривиальных математических выкладок. Нетерпеливый читатель при первом чтении может его пропустить без серьезного ущерба для дальнейшего понимания. Однако позже имеет смысл к нему вернуться, поскольку это первое место в книге, где вводятся приемы вариационного исчисления.

Допустим, мы имеем сумму полезного сигнала b (х, у) и шума и n(х, у). Наша задача — как можно точнее восстановить сигнал b (х, у). Мерой того, насколько хорошо нам это удалось сделать, будет интеграл от квадрата разности между выходным b(х, у) и искомым d (х, у) сигналами (рис. 2.11). Обычно d(x, у) - это просто Ь(х, у). Мы выбрали минимизацию интеграла от квадрата ошибки, поскольку при такой постановке задача поддается аналитическому решению. (Именно это обстоятельство, естественно, является реальной причиной популярности метода наименьших квадратов и его

203

аналогов.)

Нам нужно минимизировать квадрат ошибки

Рис. 2.11. Оптимальный фильтр, представляющий собой фильтр, который минимизирует разность между выходным о (х, у) и

требуемым d(x, у) сигналами. При этом шум п(х, у) добавляется к входному сигналу b (х, у) линейной пространственно-инвариантной системы с функцией рассеяния точки h(x, у).

Если фильтрация будет осуществляться линейной системой, то мы можем охарактеризовать ее функцией рассеяния точки h (х, у). На вход системы поступает сигнал i (х, у) = b (х, у) + п (х, у), а с

и, следовательно,

2 (x, y)dxdy

o(x, y)d (x, y) i(x , y )h( , )d (x, y)d d

и поэтому

у). Наконец, последний член имеет вид

d 2 (x, y)dxdy dd (0,0)

можем переписать выражение для минимизирующей ошибки в виде

Это выражение нужно минимизировать путем выбора импульсной функции h(х, у). Такая задача относится к вариационному исчислению. (Более подробно вариационное исчисление рассматривается в приложении.) Мы будем ее решать с помощью основного метода этого раздела математики. В типичной вариационной задаче отыскивается такое значение параметра, которое приводит к стационарному значению заданной функции. В нашем случае вместо этого необходимо найти функцию, которая дает стационарное значение заданного функционала. Функционал — это выражение, зависящее от функции, как, например, приведенная

выше величина Е зависит от h( , ) .

Допустим, что функция h (х, у) обеспечивает минимальное значение Е, и пусть 8h (х, у) — произвольная функция, используемая для изменения h (х, у). Тогда независимо от выбора 8h (х, у) функция

h(x, y) h(x, y) приведет к значению функционала, которое не может быть меньше Е. Пусть это значение равно Е + 8E. Если мы

мы могли бы уменьшить Е, добавив к h (х, у) вариацию 8h(х, у), умноженную на малую скалярную величину, и тем самым вошли бы в противоречие с предположением об оптимальности h(х, у). Далее

уравнение относительно функции h (х, у) можно решить, используя

энергетические спектры. Таким образом, чтобы в рамках принятых допущений построить систему, восстанавливающую изображение, достаточно знать эти спектры. Одна и та же система будет оптимальной не для одного, а целого класса изображений. (Иначе она, естественно, и не представляла бы особого интереса.)

В качестве примера рассмотрим систему, подавляющую шум, т. е. такую систему, на вход которой поступает сумма изображения b (х, у) и шума п(х, у), а на выходе формируется сигнал о(х, у), ближайший (в смысле метода наименьших квадратов) к исходному

207

изображению b (х, у}. Здесь d (х, у) = b (х, у) и i (х, у) = b (х, у) + п (х.

Теперь допустим, что шум не коррелирует с полезным сигналом, т.

как работает оптимальный фильтр. В тех частях спектра, где

отношение сигнал — шум bb / nn велико, усиление почти равно единице; в частях, где превалирует шум, коэффициент усиления

очень мал и равен приблизительно bb / nn , т. е. просто отношению полезного сигнала к шуму.

Теперь рассмотрим случай, когда перед сложением с шумом сигнал b (х, у) пропускается сквозь систему с функцией рассеяния

точки h (х, у). Результат i b h n необходимо пропустить через систему с функцией рассеяния точки h'(х, у). Необходимо, чтобы

внимание на совпадение этого результата с ранее полученным эвристически.

Наконец, может оказаться поучительным рассмотреть оптимальный фильтр для восстановления не исходного изображения, а уже прошедшего определенную обработку. Допустим, нам нужно оценить по методу наименьших квадратов

208

где P(u, v) - преобразование Фурье функции р (х, у). Таким образом,

собой просто каскад оптимального фильтра, восстанавливающего изображение b (х, у), и обрабатывающего фильтра Р (u, v). Ничего другого и не требуется.

Здесь необходимо указать на то, что в нашем случае построение оптимального фильтра намного проще, чем в одномерном случае.

Дело в том, что в одномерной системе импульсный отклик должен быть однонаправленным, так как он не может опережать входной сигнал. Ограничения во временной области не так просто выразить через ограничения в частотной области. Например, ограничение f (t) = 0 при t < О трудно выразить через функцию F(w), представляющую собой преобразование Фурье функции f(t). К счастью, в случае изображений подобной проблемы не существует, поскольку носитель функции рассеяния точки может распространяться от начала координат по всем направлениям. Носителем функции называется множество точек, в которых эта функция не равна нулю.

2.2.14. Модели изображений

Чтобы использовать методы оптимальной фильтрации, нам необходимо оценить энергетические спектры обрабатываемых изображений. Изучение спектров нескольких «типичных» изображений[48,49,50]быстро убедит вас в том, что основная часть энергии приходится на низкие частоты. Полезно знать о таком затухании энергии с ростом частоты, поскольку это помогает отделить требуемый сигнал от шума, имеющего плоский спектр.

209

Наблюдаемое уменьшение энергии с ростом частоты частично обусловлено тем фактом, что многие объекты или их части непроницаемы и обладают почти равномерной яркостью. Соответствующие участки изображения отделяются перепадами яркости вдоль тех краев, где объекты загораживают друг друга.

Подробное обсуждение моделей изображения выходит за рамки настоящей книги, однако основную идею можно уловить, рассматривая простой прямоугольный участок:

Преобразование Фурье такой функции имеет вид

F(u, v) = WH sin(uW)sin(vH)/(uWvH). Сдвиг участка приводит к изменению лишь фазы, а не амплитуды преобразования. Не обращая внимания на колебания, мы видим, что преобразование затухает как 1/(uv). Таким образом, в зависимости от выбора направления в

частотной области, затухание будет пропорционально либо 1/ ,

Другой полезной составной частью модели изображения мог бы стать круговой участок

многоугольные или круговые участки, как правило, затухают пропорционально некоторой степени частоты. На высоких частотах реальные изображения затухают еще сильнее, что обусловлено ограничением разрешающей способности системы. Например, в телескопах существует абсолютная верхняя граница частоты (определяемая отношением диаметра апертуры к длине световой волны), выше которой волны вообще не пропускаются. Микроскопам свойственно аналогичное абсолютное ограничение, определяемое числовой апертурой объектива и длиной световой волны.

Другое приложение того обстоятельства, что основная часть энергии изображений приходится на низкие частоты, можно найти в сфере воспроизведения изображений. Способы воспроизведения изображений, например полутоновая печать, фоторепродукция и телевидение, имеют ограниченный динамический диапазон, т. е. с их помощью можно воспроизвести лишь ограниченный диапазон уровней яркости. Если говорить о качестве воспроизведения, то нас прежде всего интересует отношение самого яркого уровня к самому темному. При воспроизведении изображений важна различимость небольших перепадов яркости. Даже значительные перепады яркости между соседними областями могут оказаться незаметными, если сами области очень ярки. Важна относительная величина перепада, т. е. отношение разности яркостей к меньшей из них. Именно поэтому динамический диапазон измеряется отношением самого яркого уровня к самому темному, а не их разностью.

Динамический диапазон цветных диапозитивов может достигать более ста к одному, тогда как газетной печати — обычно не более десяти к одному. Естественные изображения, как правило, имеют большие динамические диапазоны. При их воспроизведении часто приходится идти на компромисс. Обычно если мы пытаемся поддерживать неизменными средние значения яркости, то самые яркие и самые темные участки будут воспроизведены неточно. Чтобы из-за насыщения не утратить деталей на сильно освещенных и затененных участках, динамический диапазон необходимо сжать.

Подобное сжатие можно осуществить с помощью показательной функции. Если яркость репродукции описывается функцией b' (х, у), а оригинала — функцией b(х, у), то b' (х, у) =[b(х, у)]т, где 0 < у < 1. Так репродукция в общем оказывается

211

приемлемой, хотя легкоразличимые перепады яркости на оригинале будут незаметны на репродукции.

Другой подход состоит в использовании того обстоятельства, что изображения, как правило, содержат обширные низкочастотные участки. Фильтр, подавляющий низкие частоты, можно построить путем вычитания из изображения его сглаженной копии. В большинстве случаев

такой фильтр будет сужать динамический диапазон, Примером служит фильтр с функцией рассеяния точки

при 0 < k < 1. Его передаточная функция имеет вид

Можно применять и другие сглаживающие функции. Фотографический метод достижения подобного эффекта называется мягким маскированием. Здесь из оригинала частично «вычитается» расфокусированное изображение. Заметьте, что в этом случае резкие края воспроизводятся с полным контрастом. Однако мы должны осторожно использовать этот процесс, поскольку значения яркости смещаются от своего нормального уровня, в результате чего на изображениях объектов могут возникнуть ложные изменения. Как мы увидим позже, значения яркости используются, например, при восстановлении формы поверхности.

2.3. Обработка дискретных изображений

212

Чтобы в этом убедиться, представим, что плоскость экрана покрыта копиями заданного изображения. Иными словами, мы расширяем наше изображение до периодической в обоих направлениях функции

На практике мы имеем дело с изображениями, которые имеют ограниченные размеры и в то же время отсчитываются в дискретном наборе точек. Поэтому методы, разработанные до сих пор, необходимо приспособить, расширить и модифицировать так, чтобы их можно было применить и в такой области. Возникает также и несколько новых моментов, требующих аккуратного рассмотрения.

Теорема отсчетов говорит о том, при каких условиях по дискретному набору значений можно точно восстановить непрерывное изображение. Мы также узнаем, что происходит, когда условия ее применимости не выполняются. Все это имеет прямое отношение к разработке зрительных систем.

Методы, требующие перехода к частотной области, стали популярными частично благодаря алгоритмам быстрого вычисления дискретного преобразования Фурье. Однако нужно соблюдать осторожность, поскольку эти методы предполагают наличие периодического сигнала. Мы обсудим, как можно удовлетворить этому требованию и к чему приводит его нарушение.

2.3.1. Ограничение размеров изображения

На практике изображения всегда имеют конечные размеры. Рассмотрим прямоугольное изображение шириной W и высотой Н. Теперь нет необходимости брать интегралы в преобразовании Фурье в бесконечных пределах:

Любопытно, что для восстановления функции f(х, у) нам

213

необязательно знать F(и, v) на всех частотах. Знание того, что f(х, у)

= О при | x | W / 2 и [ у | > H/2, представляет собой жесткое ограничение. Иными словами, функция, отличная от нуля только в ограниченной области плоскости изображения, содержит гораздо меньше информации, чем функция, не обладающая этим свойством.

Чтобы в этом убедиться, представим, что плоскость экрана покрыта копиями заданного изображения. Иными словами, мы расширяем наше изображение до периодической в обоих направлениях функции

где

Здесь [х] — наибольшее целое число, не превосходящее х. Преобразование Фурье такого размноженного изображения имеет вид

Доказано, что

образом, чтобы найти f(х, у), нам достаточно знать F (и, v) в этих точках. Однако функция f (x, y) получается из f (x, y) простым

отсечением участка, для которого | х | < W/2 и | у | < H/2. Поэтому, чтобы, восстав овить f(х, у), нам достаточно знать лишь Fkl F[(2 /W )k, (2 / H )l] для всех k и l. Это — счетное множество чисел.

Обратите внимание на то, что преобразование периодической функции оказывается дискретным. Обратное преобразование можно представить в виде ряда, поскольку

215

Другой способ убедиться в этом — рассматривать функцию f(х, у) как функцию, получающуюся обрезанием некоторой функции

определяется следующим образом:

Преобразование Фурье f(х, у) — обычная свертка преобразования Фурье f (x, y) с преобразованием Фурье w(x, у). Последнее имеет вид

Таким образом, фурье-образ f(х, у) представляет собой сильно сглаженный фурье-образ f (x, y) . Позже мы увидим, что подобную

отфильтрованную функцию можно полностью задать подходящим образом выбранными отсчетами. Значения функции в точках, отличных от точек отсчета, легко находятся путем интерполяции между отсчетами.

2.3.2. Пространственная дискретизация изображения

Если изображение дискретизовано[55,56], его яркость известна только в дискретном множестве точек. Можно считать, что

216

изображение представляет собой дискетную решетку импульсов

функция преобразуется в периодическую. Последнее означает, что мы можем отбросить ту часть F (и, v), для которой | и | > / w или | v | > / w . Для восстановления функции f(х, у) она нам не нужна.

Интересно найти обратное преобразование функции, которая в указанной области совпадает с F (и,v), а всюду вне ее равна нулю: