
3188
.pdf
следующей главе.
2.2.5. Преобразование фурье для операции свертки
Пусть |
c a |
b ; |
тогда |
преобразование |
Фурье C(u, v) |
|
функции с (х, у) имеет вид: |
|
|
|
|||
[ |
a(x |
, y |
)b( |
, |
)d d ]e i(ux |
y ) dxdy |
или |
|
|
|
|
|
|
[ |
a(x |
, y |
)e i(ux |
y ) dxdy]b( , |
)d d |
|
Таким образом,
C(u, ) A(u, )e i(u ) b( , )d d
) b( , )d d
Операция свертки в пространственной области становится операцией умножения в частотной области. В этом заключается основной довод в пользу введения сложного аппарата пространственных частот. Коммутативность и ассоциативность свертки непосредственно вытекают из соответствующих свойств умножения.
Используя почти симметрию между прямым и обратным преобразованиями, нетрудно показать, что Фурье-преобразование
произведения |
двух |
функций |
d |
= |
ab |
имеет |
вид |
D(u, ) (1/ 4 |
2 ) A(u, ) |
B(u, ) . |
Вывод |
этого |
выражения |
||
аналогичен используемому выше. |
|
|
|
|
|
||
Далее, рассмотрим свертку c |
a |
b в точке (х, у) = (0, 0): |
|
||||
c(0,0) a( ,
, )b( , )d d
)b( , )d d
Применяя обратное преобразование к функции С (u, v), мы также получаем
c(0,0) |
|
1 |
|
C(u, )dud |
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
|||
4 |
|
|
|
|
|
|
||
Поскольку С (и, v) = А (и, v) В (и, v), то |
||||||||
a( , |
|
)b( , )d d |
|
1 |
|
A(u, ) A(u, )dud |
||
|
|
|
|
|||||
|
|
|
2 |
|||||
|
|
|
|
4 |
|
|
||
Если повторить предыдущие рассуждения для функции: а(-x,- у), то вместо этого получим
a( , )b( , )d d |
|
1 |
|
A * (u, )B(u, )dud |
|
|
|
||
|
|
2 |
||
4 |
|
|
||
поскольку преобразование Фурье функции а( —х, —у) есть A*(u, v), т. е. комплексно-сопряженная функция к А (и, v). Считая функцию а(х, у) действительной, в частности, видим, что
a 2 ( , )d d |
|
1 |
|
| A(u, ) |2 |
dud |
|
|
|
|||
|
|
2 |
|||
4 |
|
|
|
||
Здесь |А(u, v)|2 = А*(u, v)A(u, v). Этот результат, устанавливающий равенство энергий в пространственной и частотной областях, известен как теорема Рэлея. Ее дискретный аналог — теорема Парсеваля.
178 |
179 |

2.2.6. Обобщенные функции и единичные импульсы
Единичный импульс  не является функцией в традиционном смысле слова, поскольку ее нельзя определить заданием ее значений для всех х и у. Тем не менее, если
не является функцией в традиционном смысле слова, поскольку ее нельзя определить заданием ее значений для всех х и у. Тем не менее, если
рассматривать  как предел последовательности функций, то он допускает согласующуюся с традиционным представлением интерпретацию. Нам нужна функция, которая так зависит от параметра, что при его стремлении к некоторому пределу ее свойства приближаются к тем, на основе которых определяется единичный импульс. Говорят, что такая последовательность определяет обобщенную функцию. Пример поможет прояснить эту идею.
как предел последовательности функций, то он допускает согласующуюся с традиционным представлением интерпретацию. Нам нужна функция, которая так зависит от параметра, что при его стремлении к некоторому пределу ее свойства приближаются к тем, на основе которых определяется единичный импульс. Говорят, что такая последовательность определяет обобщенную функцию. Пример поможет прояснить эту идею.
Рассмотрим последовательность квадратных импульсов единичного объема:
(x, y) |
1/(4 2 ),| x | |
& | y | |
|
0,| x | |
& | y | |
||
|
|||
Ясно, что |
|
|
(x, y)dxdy 1
и далее, если f(х, у) ведет себя достаточно хорошо, то
lim |
(x, y) f (x, y)dxdy lim |
1 |
|
f (x, y)dxdy |
|
2 |
|||
|
4 |
|
||
|
180 |
|
|
|
Как легко видеть, разлагая функцию f(x, у) в ряд Тейлора в точке (0,0), последнее выражение равно просто f(0,0). Кроме того,
lim (x, y) 0 |
0 для всех |
(x, y) (0,0) . Таким образом, |
|
можно считать, что последовательность функций { (x, y)} определяет единичный импульс. При вычислении интеграла,
(x, y)} определяет единичный импульс. При вычислении интеграла,
содержащего функцию |
(x, y) , мы можем заменить ее на |
(x, y) , |
||
а затем в конечном результате перейти к пределу при |
|
0 . |
|
|
Из приведенного |
вида последовательности |
(x, y) |
мы |
|
|
|
|||
заключаем, что (x, y) |
можно представить в виде произведения |
|||
двух одномерных единичных импульсов одномерный импульс определяется следующим свойством:
f (x) (x) 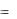 f (0)
f (0)
(x) ( y) , где фильтрующим
для любой функции f(x).
Интеграл от одномерного единичного импульса представляет
собой единичную ступенчатую функцию
1, x 0 (t)dt u(x),u(x) 1/ 2, x 0
0, x 0
И наоборот, единичный импульс можно рассматривать как производную единичной ступенчатой функции. Это легко усмотреть, если единичную функцию представить в виде предела
последовательности {u (x)}, где
(x)}, где
181

1, x 
u (x) |
1/ 2[1 (x / )],| x | |
0, x 

Откуда ясно, что
d |
u (x) |
1/ 2 ,| x | |
|
dx |
0,| x | |
||
|
Следует подчеркнуть, что одну и ту же обобщенную функцию можно определить различными последовательностями. Например, можно рассмотреть последовательность функций Гаусса
|
|
|
1 x2 |
y 2 |
|
|
|
(x, y) (1/ 2 |
2 )e 2 |
2 |
|
|
|
|
|
|
|
0 |
|
|
Функции этой последовательности охватывают единичный |
||||||
объем, а |
(x, y) стремится к нулю для всех точек (x, y) (0,0) |
|||||
при |
0 . |
Перед |
последовательностью |
(x, y) |
||
|
||||||
(x, y)
последовательность имеет то преимущество, что она всюду дифференцируема.
Чему равно преобразование Фурье единичного импульса? С одной стороны, мы имеем
(x, y)e i(ux y ) dxdy 1
y ) dxdy 1
в чем легко убедиться, подставляя в e i(ux y) значения x = 0 и y = 0 на основе фильтрующего свойства единичного импульса. Мы можем также исходить из данного выше определения:
lim |
(x, y)e i(ux y ) dxdy |
или
lim |
1 |
|
e iux dx |
1 |
|
e i y dy |
|||
2 |
2 |
||||||||
|
|
|
|
|
|
|
|||
|
lim |
sin u |
|
sin |
|
1 |
|||
|
|
|
|
||||||
т.е. |
|
|
u |
|
|
|
|||
Отсюда следует, что система, функция рассеяния точки которой представляет собой единичный импульс, является тождественной, так как она не изменяет входного сигнала. Все частоты проходят сквозь нее с единичным коэффициентом усиления, и никакого сдвига по фазе не происходит, поскольку передаточная функция Н (u, v) равна единице, т. е. выходной сигнал тождествен входному.
2.2.7. Множители сходимости и единичный импульс
Интеграл
e i(ua b) dud
b) dud
182 |
183 |

Рис. 2.4. Комплекснозначные экспоненциальные собственные функции двумерной линейной пространственно-инвариантной
системы.
не сходится. Причина в том, что колебания в подынтегральном выражении не затухают с увеличением u и v. Один из способов приписать осмысленное значение интегралу, несмотря на указанную трудность, состоит в умножении подынтегральной функции на множитель сходимости, который уменьшит ее значения для больших u и v
Отсутствие сходимости у интеграла от синусоиды (сплошная линия). Однако если подынтегральное выражение умножить на гауссову функцию (штриховая линия), то мы получим функцию, которую можно проинтегрировать. Исходный интеграл можно рассматривать как предел интеграла с множителем сходимости, становящимся плоским
Таким образом, чтобы новый интеграл приближался к исходному при стремлении параметра к некоторому определенному пределу. Значение, приписываемое исходному интегралу, полагается равным [48] пределу значений модифицированного интеграла при стремлении параметра к упомянутому пределу. Сформулированный метод станет ясен, если мы применим понятие множителя сходимости к интегралу, приведенному выше.
В этом случае удобным множителем сходимости является функция Гаусса
1 u 2  2
2
c (u, ) e 2 2
где |
|
|
|
|
|
— параметр, который будет изменяться. Заметим, что |
|||||||||||||||||||||
для |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
любой |
конечной |
точки |
(u, v) |
lim c |
(u, |
) |
|
1 |
при |
0 . |
Интеграл, |
|||||||||||||||||
который |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
необходимо вычислить, имеет вид |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
1 u 2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
e 2 |
|
|
|
2 ei(ua |
b) dud |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|||
|
|
1 |
( |
|
|
u 2 |
|
|
)2 |
iua |
|
1 |
( |
|
2 |
)2 |
iua |
|
|
|
|
|
|
||||
e 2 |
2 |
|
|
|
|
du |
e 2 |
2 |
|
|
|
d |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Теперь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
( |
|
u 2 |
|
)2 |
|
|
|
|
|
|
|
|
|
|
|
1 |
2 2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
e 2 |
2 |
|
|
|
cos(ua)du |
|
2 |
|
e 2 |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
в то время как |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
1 |
( |
u 2 |
)2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
e 2 |
2 |
|
|
|
sin(ua)du 0 |
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
поскольку sin(ua) — нечетная функция от и. Поэтому весь |
|||||||||||||||||||||||||||
интеграл равен |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
1 |
(a2 b2 ) 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
2 e 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Он стремится к нулю при |
|
|
|
|
, |
если только a2 |
b2 0 . |
||||||||||||||||||||
Однако при а = b = 0 результат не стремится к конечному пределу при .
Следовательно, интеграл
184 |
185 |

ei(ua b) dud
b) dud
должен быть пропорционален единичному импульсу (a,b) . Но чему равен коэффициент пропорциональности?
Поскольку
(a, b)dadb 1
мы можем определить этот коэффициент, если вычислим
|
1 |
(a2 |
b2 ) |
2 |
||
|
|
|
|
|||
lim |
2 2 e 2 |
dadb |
||||
|
|
|||||
Двойной интеграл можно представить в виде произведения двух простых интегралов и получить выражение
1 a2 2 |
1 b2 |
2 |
||||
|
|
|
|
|
|
|
2 2 e 2 |
da e 2 |
db 4 2 |
||||
Произведение не зависит от , и окончательно мы имеем
ei(ua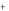 b) dud
b) dud 4 2 (a, b)
4 2 (a, b)
Этот результат мы уже использовали во время обсуждения преобразования Фурье.
186
2.2.8. Частные производные и свертка
Для выделения краев на изображениях мы используем дифференцирование, и поэтому интересно будет узнать, как связаны преобразования Фурье исходного и дифференцированного изображений. Иными словами, если F(u, v) — преобразование Фурье для функции f(х, у), то каковы преобразования Фурье для
операторов |
|
f / x и f / y Рассмотрим преобразование |
|
||||||||||
|
|
|
|
|
f |
e i(ux |
y ) dxdy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x |
или |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
[ |
|
|
|
f |
e iux dx]e i y dy |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
x |
|
|
|
|
|
|
||
Внутренний интеграл берется интегрированием по частям |
|||||||||||||
|
f |
e iux dx |
[ f (x, y)e iux dy] |
(iu) |
f (x, y)e iux dx |
|
|||||||
|
|
|
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|||
Однако следующий |
шаг мы |
сможем |
предпринять |
только |
|||||||||
тогда, когда |
f (x, y) |
0 |
при |
x |
. В этом |
случае |
|||||||
|
|
|
|||||||||||
преобразование Фурье имеет вид:
(iu) f (x, y)e i(ux y ) dxdy iuF(u, )
y ) dxdy iuF(u, )
Если f(х, .у) не стремится к нулю на бесконечности, интеграл не сходится, но при этом мы можем прибегнуть к множителям сходимости и получить тот же результат. Подобным же способом
легко показать, что преобразование Фурье для оператора |
f / y |
|
|
187 |
|

равно i |
F(u, ) . Отсюда заключаем, что |
дифференцирование |
||
выделяет |
высокочастотные |
компоненты |
и |
подавляет |
низкочастотные. В частности, любой постоянный фон или состав-
ляющая с нулевой частотой полностью теряется. |
|
|
|||||||
|
Лапласиан |
функции |
f(х, |
у) |
определяется |
|
как |
||
2 f |
2 f / dx2 |
2 f / dy2 |
Следовательно, преобразование Фурье |
||||||
лапласиана равняется |
(u 2 |
2 )F (u, ) |
. Выражение — (u |
2 |
2 |
||||
|
|
|
|
+ v ) |
|||||
можно рассматривать как передаточную функцию оператора |
2 в |
||||||||
смысле, который станет ясен в дальнейшем. Обратим внимание на круговую симметрию этой передаточной функции: она зависит только от (u2 + v2), а не по отдельности от u и v. Это наводит на мысль о том, что и сам оператор Лапласа обладает круговой
симметрией. |
|
|
|
|
Может |
показаться |
странным |
совпадением, |
что |
дифференцированию в пространственной |
области соответствует |
|||
умножение |
в частотной области, поскольку раньше мы уже |
|||
наблюдали подобное же соответствие между сверткой и умножением. Такое совпадение становится менее удивительным, если представить результат дифференцирования как реакцию линейной пространственно-инвариантной системы! Возможно ли, что дифференцирование эквивалентно свертке с некоторой особенной функцией? (Эта функция должна быть действительно особенной, поскольку ввиду локального характера операции дифференцирования она должна равняться нулю всюду, кроме начала координат.) Изучим этот вопрос более подробно.
Передаточной функцией Н(u, v), соответствующей первой частной производной по х, является iu. Используя обратное преобразование Фурье к iu, мы можем найти функцию рассеяния точки, соответствующую первой частной производной
|
1 |
|
iue i(ux y) dud |
|
|
|
|
4 |
|
2 |
|
|
|
Этот интеграл не сходится. Его можно было бы взять с помощью множителя сходимости, однако проще заметить, что
188
iue i(ux y ) dud |
4 2 |
(x, y) |
Следовательно, интеграл |
равен ( / x) (x, y) , поскольку |
|
умножению преобразования Фурье на iu соответствует
дифференцирование по х. Поскольку  — необычная функция, то нельзя ожидать, что ее производная окажется функцией в классическом смысле. Однако ее можно найти с помощью последовательности функций, например таких:
— необычная функция, то нельзя ожидать, что ее производная окажется функцией в классическом смысле. Однако ее можно найти с помощью последовательности функций, например таких:
|
|
|
|
|
|
x |
|
1 x2 |
y2 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x, y) |
|
|
|
|
e 2 |
|
2 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
4 |
|
|
|
|
|
|||
|
x |
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Равнозначный способ ее определения — в виде предела |
||||||||||||||
последовательности |
|
|
|
|
|
|
|
|
|
|||||
|
x, (x, y) |
|
1 |
[ (x |
|
, y) |
|
(x |
, y)] |
|
||||
|
|
|
|
|
|
|||||||||
|
|
|
||||||||||||
Здесь мы имеем два близко расположенных импульса |
||||||||||||||
противоположной |
полярности. Результат, называемый |
дуплетом, |
||||||||||||
будет обозначаться |
x |
(x, y) |
. |
Это |
определение |
аналогично |
||||||||
|
|
|
|
|||||||||||
обычному способу определения частной производной как предела приращения функции
f (x, y) |
|
f (x |
, y) f (x |
, y) |
|
|
|||
|
|
|
|
|
|
|
|
||
x. |
2 |
|
|
|
|
|
|||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
так что |
|
|
|
|
|
|
|
|
|
lim f (x, y) |
x. (x, y) |
f (x, y) |
|
(x, y) |
f |
||||
x. |
|
|
|||||||
x |
|||||||||
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
189

Рис. 2.5. Действие оператора Лапласа, рассматриваемое как предел последовательности операций свертки с функциями, обладающими круговой симметрией по отношению к началу координат.
Обобщенную функцию, соответствующую лапласиану, можно представить в виде предела следующей последовательности,
получаемой, например, дифференцированием  (x, y) (рис. 2.5):
(x, y) (рис. 2.5):
|
x 2 |
|
y 2 |
2 |
1 x2 y 2 |
|
|
|||
|
|
|
|
|
|
|
|
|||
L (x, y) |
|
|
e 2 |
2 |
|
|
|
|||
|
2 |
6 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
Эта функция обладает круговой симметрией. В центре |
||||||||||
симметрии имеется впадина глубиной 1/(2 4 ) |
и радиусом |
, по |
||||||||
краям которой расположено |
|
кольцеобразное |
возвышение |
с |
||||||
максимальной высотой e 3 / 2 /( 4 ) и радиусом 
 3
3 .
.
В дальнейшем при работе с дискретными аналогами этих непрерывных операторов она нам пригодится.
2.2.9. Круговая симметрия и изотропные операторы
Лапласиан представляет собой линейную комбинацию частных производных наименьшего порядка, обладающую круговой симметрией. Это означает, что результаты применения лапласиана к повернутому изображению и повернутого лапласиана к исходному изображению совпадают. И наоборот, если мы повернем изображение, применим оператор Лапласа и повернем
190
получившееся изображение назад, то получим тот же результат, что и при простом применении лапласиана.
Другим оператором второго порядка с круговой симметрией
является |
квадратичная |
вариация |
|
( 2 / x 2 )2 |
2( 2 / x y)( 2 / y x) ( 2 / y 2 )2 . |
Однако |
этот |
оператор нелинеен. Если мы допустим нелинейность, то
дифференциальным |
оператором |
с |
круговой |
симметрией |
||
наименьшего |
порядка |
будет |
|
квадрат |
градиента |
|
( 2 / x 2 )2 ( 2 / y 2 )2 .
Операторы, обладающие круговой симметрией, привлекательны тем, что результат их применения к изображению не зависит от ориентации последнего. Кроме того, функцию, обладающую круговой симметрией, можно описать простым плоским профилем, а не поверхностью. Наконец, как сейчас будет показано, преобразование Фурье такой функции вычисляется с помощью однократного, а не двойного интегрирования.
Введем полярные координаты как в пространственной, так и
частотной областях (рис. 2.6): |
x |
r cos |
, y r sin |
, |
sin |
, |
так что ux y r cos( |
) . |
Теперь |
если f(x, |
у) |
=f(r), |
то |
преобразование Фурье |
|
|
|
|
|
|
Рис. 2.6. Удобство введения полярных координат как в пространственной, так и в частотной областях при работе с
функциями, обладающими круговой симметрией.
191

F (u, ) f (x, y)e i(ux y ) dxdy
y ) dxdy
примет вид
F ( ) r f (r)e ir cos( ) drd
) drd
0
(Величина r в подынтегральном выражении — это просто определитель якобиана преобразования от декартовых координат к полярным.) Если поменять порядок интегрирования, то после очевидной замены переменных внутренний интеграл примет вид:
e ir cos( ) d |
2 cos(r cos )d |
2 J |
0 |
(r ) |
|
|
|
|
|
|
0 |
|
|
|
где J0 (х)_— функция Бесселя нулевого порядка. Следовательно, если F(u, v)=F(p), то
Рис. 2.7. Функция
J0 (z)/z, играющая в двумерных системах ту же роль, что и функция sin(z)/z — в одномерных.
192
F( ) 2 r f (r)J 0 (r )dr
0
Аналогично можно показать, что
|
|
1 |
|
|
|
|
|
|
f (r) |
|
f ( )J |
0 |
(r )d |
||||
|
|
|||||||
2 |
||||||||
|
|
0 |
|
|
|
|
||
|
|
|
|
|
|
|
||
Две последние формулы определяют преобразование Ганкеля. (Причина их асимметричности кроется в асимметричности нашего определения преобразований Фурье.)
Мы видим, что преобразование Фурье функции с круговой симметрией также обладает круговой симметрией. Кроме того, оно является действительной функцией, откуда следует, что сдвиг по фазе равен нулю.
Этими выводами мы воспользуемся при анализе некоторых простых дефектов зрительной системы. В качестве примера рассмотрим импульсную функцию системы, которая действует как фильтр нижних частот с частотой среза В, т. е.
|
|
1, |
B |
|
H ( ) |
||||
|
|
|||
0, |
B |
|||
|
|
|||
Производя обратное преобразование, получим
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
h(r) |
|
H ( )J 0 (r )d |
J |
0 |
(r )d |
|||||||
|
|
|
|
|||||||||
2 |
|
|
2 |
|||||||||
|
|
|
|
0 |
|
|
|
0 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
Пусть z r |
|
, тогда |
|
|
|
|
||||||
193

|
|
|
|
|
1 |
|
rB |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
h(r) |
|
|
|
zJ |
0 |
(z)dz |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
2 r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Далее |
(d / dz)zJ1 (z) |
zJ0 |
|
zJ0 |
(z) |
, |
где |
J |
1 |
(z) |
- |
функция |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Бесселя I порядка. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
2 J1 (rB) |
|
|
|
|
|
|||||
h(r) |
|
|
|
(rB)J |
1 |
(rB) |
|
B |
|
|
|
|
|
|||||||||||||
|
2 |
r 2 |
|
2 |
|
|
|
(rB) |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
Можно |
доказать, что |
lim J1 (z) / z |
1/ 2(z |
|
|
) . |
Поэтому |
||||||||||||||||||
h(r) имеет максимум в начале координат, а затем плавно убывает до нуля при z = = 3,83171... (рис. 2.7). Потом она становится отрицательной и в дальнейшем осциллирует около нуля со все убывающей амплитудой. Асимптотически снижение амплитуды
описывается функцией z-3/2. Функция J1 (z) / z для двумерных систем играет ту же роль, что и функция sin (z)/z для одномерных.
Между прочим[49,50,51], должно быть ясно, что фильтр со слишком крутым срезом приведет к возникновению колебаний или «кольцевых» эффектов в пространственной области (иногда называемых явлениями Гиббса). Во многих случаях предпочтительнее фильтр с более плавным понижением, поскольку он меньше подвержен воздействию указанных явлений. Например, гауссов фильтр имеет очень плавный срез, который захватывает заметный интервал частот. Он не порождает никаких ложных изменений в отфильтрованном изображении.
2.2.10.Размывание, расфокусировка и скоростной смаз
Вобычной зрительной системе оказывается, что лучи, которые в идеальных условиях должны были бы фокусироваться в одной точке, в действительности немного расходятся. Такое «размывание» изображения может принимать различные формы,
194
однако иногда его можно смоделировать гауссовой функцией рассеяния точки, нормированной на единичный объем:
|
1 |
|
1 x2 y2 |
||
|
|
|
|
|
|
h(x, y) |
|
e 2 |
2 |
||
|
|
|
|||
2 |
2 |
|
|||
|
|
|
|
||
|
|
|
|
|
|
Поскольку эта функция зависит от х2 + у2, а не по отдельности от х или у, она обладает круговой симметрией. Преобразование Фурье для нее можно вычислить с помощью формулы Ганкеля.
Однако заметим, что функция Гаусса распадается на произведение двух функций от х и от у. Поэтому другой подход может оказаться менее трудным:
|
|
|
|
|
|
|
1 |
|
|
|
1 x2 |
y2 |
|
|
|
||
H (u, |
) |
|
|
|
|
e 2 |
2 e i(ux |
y) dxdy |
|||||||||
|
|
2 |
|||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
1 x2 |
|
|
|
|
1 |
1 |
y2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
e 2 2 e |
iux dx |
|
|
|
e 2 |
y 2 e i y dy |
||||||||||
|
|
|
|
|
|
|
|||||||||||
2 |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Первый интеграл в правой, части равен
|
1 |
|
1 x2 |
1 |
u |
2 2 |
|||
|
|
|
|
|
e |
|
|
||
|
|
e 2 2 cos(ux)dx |
2 |
|
|||||
|
|
|
|
||||||
|
2 |
|
|||||||
|
|
|
|
|
|
|
|
|
|
195

Рис. 2.8. Эквивалентность расфокусировки изображения и его свертки с функцией, обладающей круговой симметрией.
График последней ограничивает единичный объем и напоминает цилиндрическую коробочку
Поэтому в итоге получаем, как и должно быть функцию с круговой симметрией:
1 |
(u 2 2 ) 2 |
||
|
|
||
H (u, ) e 2 |
|||
|
|||
Мы видим, что низкие частоты проходят непогашенными, в то время как высокие частоты уменьшаются по амплитуде, это
особенно заметно у частот выше примерно 1/ . Но  — характерный размер исходной функции рассеяния точки, следовательно, чем больше величина размывания, тем ниже подавляемые частоты. Это пример обратной зависимости между изменениями масштабов в пространственной и частотной областях.
— характерный размер исходной функции рассеяния точки, следовательно, чем больше величина размывания, тем ниже подавляемые частоты. Это пример обратной зависимости между изменениями масштабов в пространственной и частотной областях.
В самом деле, если r — характерный радиус пятна в пространственной области, а — его размер после
преобразования, то r — величина постоянная.
Один из способов размывания изображения заключается в его расфокусировке. В этом случае функция рассеяния точки представляет собой небольшую цилиндрическую коробочку, в чем можно убедиться, если рассмотреть конус лучей, проходящих через линзу, с вершиной в фокусе. (Эта точка не принадлежит плоскости изображения, а находится несколько впереди или сзади от нее.) Плоскость изображения пересекает этот конус по окружности. Внутри нее яркость постоянна (рис. 2.8), и, следовательно, мы имеем
h(x, y) |
1/( R2 ), x2 |
y 2 |
R2 |
|
0, x2 y 2 |
R2 |
|
|
|
|
|
|
||
здесь R 1/ 2(d / f ')e , |
где |
d — диаметр линзы; f' — |
||
расстояние от линзы до точки точной фокусировки, а е — смещение
плоскости изображения. Мы можем применить преобразование Ганкеля и получить формулу
|
|
|
2 |
R rJ |
|
(r )dr 2 |
J1 (R ) |
|
|
H ( ) |
0 |
||||||
|
|
|
||||||
|
|
|
R2 |
|
(R ) |
|||
|
|
|
|
|
||||
|
|
|
0 |
|
|
|
|
|
в которой используется упоминавшееся ранее соотношение |
||||||||
(d / dz)zJ1 (z) |
zJ0 (z) |
. При этом снова низкие частоты проходят |
||||||
|
|
|
|
|
|
|||
свободно, а верхние срезаются по амплитуде, причем некоторые вообще не пропускаются. Другие инвертируются, поскольку функция J1 (z) колеблется около нуля. На частотах, для которых
J1 (R ) 0 , как мы видим, светлые участки расфокусированного изображения совпадают с темными участками идеального изображения и наоборот. Компоненты изображения с частотами, для
которых J1 (R ) 0 , гасятся полностью. Такие компоненты невозможно восстановить по расфокусированному изображению. Как упоминалось выше, первый нуль функции J1 (z) появляется при 2 = 3,83171.... Мы снова наблюдаем обратную зависимость между пространственной и частотной областями, поскольку теперь мы
имеем z (R ) , |
т. е., чем больше радиус расфокусировки R, тем |
меньше частота |
, при которой J1 (R ) 0 . |
Другой тип |
ухудшения изображения обусловлен движением. |
При этом может двигаться как зрительная система, так и наблюдаемые объекты. В обоих случаях точка на изображении смазывается, превращаясь в черточку. Допустим для удобства, что движение происходит вдоль оси х, а длина черточки равна 2l. Тогда функцию рассеяния точки можно представить в виде произведения
hx |
(x, y) [u(x l) u(x l)] ( y) / 2l |
, где, как и ранее, и u(z) — |
|
|
единичная ступенчатая функция. Здесь функция рассеяния точки не обладает круговой симметрией. Ее преобразование Фурье можно найти следующим образом:
197
