Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2748

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

2.2 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

первая из которых зависит только от аргумента

а вторая –

только от t.

Находя вторые производные от соотношения

68 по x

и по t, в результате подстановки их в уравнение

полу-

чим

X x T

t X x T t ,

x T

t X x T t ,

X x T t a

X x T t ,

или

1 T t

X x

T t

X x

Соотношение

должно

выполняться

при

любых

x 0, l и t

0. Отличительная

черта соотношения 69 –

возможность разделения переменных, то есть левая часть этого равенства зависит только от t, а правая – только от x. То-

гда, при условии, к примеру, фиксации

правая часть, а,

следовательно, и левая обязаны сохранять постоянное значение при любых значениях t. Точно также левая часть, а вме-

сте с ней и правая часть соотношения при фиксации

долж-

ны сохраняться при изменении x. Отсюда следует, что соотношение 69 выполнимо только тогда, когда обе его части не зависят ни от x, ни от t, то есть являются постоянной ве-

личиной. Придав данной константе разделения символ					со
знаком минус, запишем 69 в форме
	1 T t		X x
				.	70
	a2	T t	X x	.	70
			51

Следовательно, функции

T t

X x

представляется

возможным найти, решая обыкновенные дифференциальные уравнения с постоянными коэффициентами

	T t a2T t 0; X x X x 0.
	С целью выполнения для частных решений в форме
68	граничных условий 67	для всякого t 0 должны удо-
влетворяться условия X 0 0		и X l 0.
	Тогда для нахождения координатной функции X x

нужно решить такую задачу: дифференциальное уравнение

X x X x

решить линейное однородное

0, 0 x l,	71

для которого на границах

X 0

x 0 и

0, X l

x l0.

выполняются условия

Для каждого ненулевое решение

const

X x 0.

для данной задачи существует Однако, для некоторых значе-

ний константы 0	для задачи 71 ,	72 существуют и
ненулевые решения.	Данные значения		именуются соб-

ственными значениями, а отвечающие им ненулевые решения

X x – собственными функциями задачи 71 , 72 . Задача

определения собственных значений и собственных функций именуется задачей Штурма-Лиувилля.

Рассматривая снова задачу 71 и 72 , исследуем все

варианты, когда константа разделяющая постоянная нулевая, меньше нуля или больше нуля.

В случае

общее решение уравнения

пред-

ставляет собой линейную функцию X торой оба условия 72 выполняются

x C1x C2 ,

для ко-

только тогда, когда

C172

C2 0. Следовательно, в случае 0 для задачи
существует лишь нулевое решение X x 0.
В случае 0 то общее решение уравнения	71

71 ,

X x C e		x
X x C e
1

при подстановке в граничные данные ма

C e	x
C e
2
72	получается систе-

C C

C e

Поскольку детерминант данной однородной системы

D e

l e l

e l

для

каждого

0 отличен от нуля,

она имеет только одно

решение C1

C2 0.

Таким образом,

для задачи 71 ,

не существует отрицательных собственных чисел.

При

общее

решения

уравнения

X x C1 cos

x C2 sin

x может удовлетворить гранич-

ным условиям

0 C 0;

l C cos

l C sin

l 0

при

C1 0,

но C2 C 0, если определитель системы

D sin

l 0,

что выполняется

образом, только для собственных

n 2 , n n

при

чисел

l n, n N.

Таким

задача	71 ,	72		имеет в роли ненулевых решений семей-
ство собственных функций
		X		x sin	nx		, n N,
		X	n	x sin	l		, n N,			75
					l


ортогональных на промежутке 0, l .
Любому		собственному				числу		n отвечает	функция
Tn t ,	определяемая					из		решения	уравнения

	n			2
	n				2		t
T t					a T		t
n		l			n
		l
форме
			T		t	a
				n			n

0.	Его общее решение записывается в

cos	na	t b sin	na	t,	76


	l	n	l

здесь

an и bn – произвольные константы.
После подстановки соотношений 75	и 76 в выра-

жение

68 ,

определим частные решения

уравнения

65 ,

для которых выполняются граничные данные

67 .

Тогда

любому n N соответствует решение

x, t

cos

b sin

sin

Наложение всех решений в форме

u x, t

a cos

t b sin

sin

n 1

тоже есть решение уравнения 65 , для которого выполняются граничные данные 67 , в этом случае представляется возможным подыскать константы an и bn в уравнении 78 при условии выполнения для функции в виде ряда 78

начальных данных

66 .

С этой целью продифференцируем

почленно ряд

по t :

a sin

t b

cos

sin

n 1

и для t 0

потребуем выполнения начальных данных

x , 0 x l;

t 0

sin

n 1

b sin

x , 0 x

t 0

n 1

Соотношения

есть разложение исходных функций

и x

в ряды Фурье по ортогональной в промежутке

x0, l


системе тригонометрических функций		nx		Тогда
системе тригонометрических функций	sin		.	Тогда
		l	n 1

коэффициенты an	и	na		bn	данных разложений есть коэф-
			l

фициенты Фурье	n	и	n		функций x и x . Находя

данные коэффициенты с использованием формул ЭйлераФурье, имеем

x sin

dx;

x sin

dx.

Следовательно,

ряд

с коэффициентами

bn ,

определѐнными по выражениям краевой задачи 65 – 67 .

80 ,

даѐт решение заданной

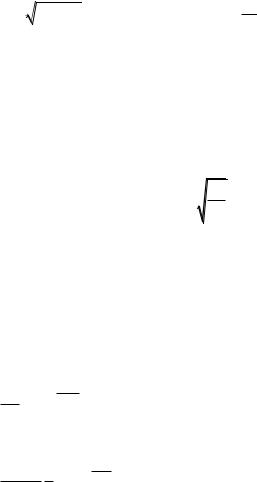
ду:

где

Решение 78

можно преобразовать к следующему ви-

u x, t un x, t n cos nt n sin

n 1

;

arctg

Каждое из слагаемых

un x, t в уравнении

описы-

вает движение струны в виде стоячей волны, которая образуется в результате наложения прямой и обратной бегущих волн при отражении их от концов струны. Эти стоячие волны называются простыми тонами или гармониками.

В стоячей волне все частицы струны колеблются с одинаковой частотой

	n	,	a	T		.
	n	,		0		.
				0
n	1	1	l
			l		0
					0

Эти частоты n , n N, называются ми колебаний ограниченной струны.

собственными частота-

Самая низкая частота 1

соответствует основному тону струны, а более высокие частоты, кратные 1 , соответствуют обертонам. Изменяя длину

струны или силу еѐ натяжения T0 , можно изменять частоты колебаний n .

	Для		n -ой стоячей волны точки струны с координатами
xm	ml	, m 0, n, в которых sin		nx	0,
				m		остаются всѐ время
	n			l

неподвижными. Они называются узлами стоячей волны (рис.

7,	тѐмные		точки).	Точки струны с координатами
xm	2m 1 l		, m 1, n,	совершают колебания с максимальной
xm	2	n	, m 1, n,	совершают колебания с максимальной
	2	n
				56

амплитудой, равной n . Такие точки носят название пучностей стоячей волны (рис. 7, светлые точки).

Рис. 7. Стоячие волны

Пример 1. Решить однородное волновое уравнение

, t 0, 0 x 1,

с начальными данными

t 0

x 1 x , 0 x 1,

и однородными граничными данными

x 0

0, u

x l

0, t 0.

Решение.

1. Находим ненулевое решение заданного уравнения в форме произведения двух функций

u x, t X x T t .

Определяя вторые производные этого выражения по x и по

t, в результате подстановки их в заданное уравнение имеем
2u		X x T t X x T t ,
t2	t	X x T t X x T t ,
		57

X x T t X x T t ,

X x T t 4X x T t ,

или

T t

X x

4 T t

X x

Поэтому функции

T t

X x

являются решениями обык-

новенных дифференциальных уравнений T

t 4T t 0;

X x X x 0, X 0 X 1 0.

2. Решаем задачу

x X x 0, X 0 X 1 0.

k 2 0, k 2 , k

1, 2

X x C1 cos

x C2 sin

X 0 C 0

;

X 1 C sin

x sin nx, n N.

Каждому собственному значению n

соответствует функция

Tn t ,

которую

находим

из

решения

уравнения

Tn t 4 2n2Tn t 0. Общее решение данного уравнения за-

писывается в форме	T	t a	cos 2 nt b sin 2 nt,	здесь	a	n
	n	n	n			n

иbn – произвольные константы.

3.Решение исходной краевой задачи ищем в виде

u x, t an cos 2 nt bn sin 2 nt sin nx,

n 1

u t 0 0, u t 0 x 1 x , u x 0 u x 1 0.


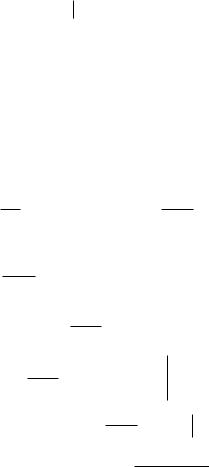
u	t 0	a sin nx 0, a		0.
	t 0	n	n
		n 1

Дифференцируя функцию

t
t		2
u		2
	n 1

u	по t
nb cos
	n

, получим 2 nt sin nx;

ut t 0 2 nbn sin nx x 1 x .

n 1

Определяя коэффициенты																	bn
получаем
	1			1		x 1 x sin nxdx
n	1
n
b	n
	n			0
				0
		1						x		2	x cos nx
										2
			n
		2	n		2

												1			1
												1			1		2
												3	n	3	1		2
													n		0
															0
							1				1 2x					sin
							1				1 2x					sin
								n
							3	n	3

по формулам Эйлера – Фурье,

		1				1
		1			2	x		2	x d cos nx
		2			2	x			x d cos nx

	n					0
						0
		1


1
1				2x 1					cos nxdx
0
		0
x d sin nx
						1
		1
nx		0	2				sin nxdx
						0

Подставляя функции u,

		2			cos nx			0	;
								0
		4	n	4				1
		4		4				1

b	0, b						4			, k N.
b	0, b						2k	1	4	, k N.
2k	2k 1					4			4
						4

найденные коэффициенты в выражение для получим

		4
u x, t		4			sin 2	2k 1 t sin 2k 1 x.

	4	2k	1	4
k 0	4	2k	1

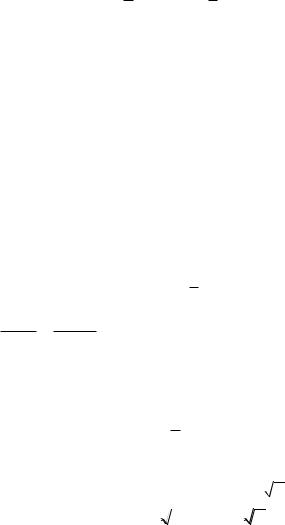
Пример 2. Решить первую смешанную задачу для волнового уравнения на отрезке.

		u	1	u , x				0,	3	, t	0, ,
		u		u , x				0,		, t	0, ,
		tt	4		xx
			4						2
					3	, ut
					3
u	t 0	x x					t 0 0, u				x 0	u		3	0.
u	t 0	x x					t 0 0, u				x 0	u		3	0.
					2								x
					2								x	2

Решение.
1. Будем		искать	нетривиальное	решение	исходного
уравнения	в	виде	произведения	двух	функций
u x, t X x T t . Дифференцируя дважды это выражение
по x и по t,	после подстановки его в исходное уравнение по-

лучим
		X x T t ,
u X x T t		X x T t ,
tt	t
	t

		u
		xx
или 4	T t	X x
или 4	T t	X x
	T t	X x

Поэтому функции

Xx T

x T tt

X x

		X x T t ,
		X x T t ,
		x
	1	X x T t ,
	4	X x T t ,
	4

являются решениями обык-

новенных дифференциальных уравнений

X x X x 0, X 0			X			3
X x X x 0, X 0			X					0.
						2
2. Решаем задачу X				x X x 0,
2. Решаем задачу X				x X x 0,
k	2	0, k			2		, k
	2				2
								1, 2
X x C1 cos
X x C1 cos						x C2 sin

4T t T t 0;

X0 X 2 0.

<<< < Предыдущая 1 2 3 4 56 / 126 7 8 9 10 11 12 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.17 Mб02738.pdf
#
15.11.20222.19 Mб12741.pdf
#
15.11.20222.19 Mб22742.pdf
#
15.11.20222.19 Mб02746.pdf
#
15.11.20222.2 Mб22747.pdf
#
15.11.20222.2 Mб42748.pdf
#
15.11.20222.2 Mб02749.pdf
#
15.11.20222.21 Mб32750.pdf
#
15.11.20222.21 Mб12753.pdf
#
15.11.20222.21 Mб22755.pdf
#
15.11.20222.22 Mб12758.pdf