
2748
.pdf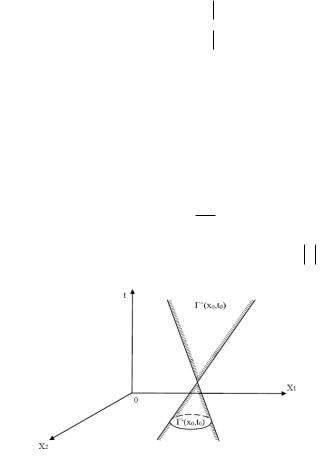
именуемая характеристическим конусом с вершиной в точке
x |
, t |
0 |
, |
0 |
|
|
является характеристикой волнового уравнения.
Характеристический конус
|
|
|
|
|
|
|
|
|
t |
|
x |
, t |
0 |
|
a |
|
|||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
t |
||||
|
x |
, t |
0 |
|
a |
|
|||
|
|
0 |
|
|
|
|
|
|
34 |
||
t |
0 |
|
|
|
|
t |
0 |
|
|
|
|
есть граница конусов
x x |
|
|
, |
|
|
|
|||
0 |
|
|
|
|
x x |
|
|
, |
|
|
|
|||
0 |
|
|
|
|
именуемых соответственно конусами будущего и прошлого с
вершиной в точке x0 , t0 (рис. 6).
. Введѐм обозначение |
|
|
|
|
|
0, 0 |
|
. |
|
|
|||||||
|
|
|
|
|
|
Для волнового
уравнения существует и иное множество характеристических поверхностей – множество касательных плоскостей к характеристическим конусам
|
|
|
|
|
at x, b C, |
|
35 |
|
в котором |
b |
|
b , b |
, ..., b |
, b , k 1, n, |
и C – произвольные |
||
|
1 |
2 |
n |
k |
||||
действительные числа, удовлетворяющие условию |
b 1. |
|||||||
Рис. 6. Характеристический конус
31
б) Уравнение теплопроводности |
u |
2 |
u f . |
Его ха- |
t |
a |
|||
|
|
|
|
|
рактеристиками является множество плоскостей t C. |
|
|||
в) Уравнение Пуассона u f . |
Оно не имеет действи- |
|||
тельных характеристик, так как из характеристического урав-
|
n |
|
|
2 |
|
|
|
||||
нения |
|
x |
|
0 |
|
|
i 1 |
|
|
||
|
i |
|
|||
что невозможно.
на
0
следует
grad 0
на
0,
Вопросы для повторения
1.Порядок уравнения в частных производных.
2.Общий вид уравнения в частных производных второго порядка.
3.Квазилинейное уравнение.
4.Линейное уравнение. Линейное уравнение с постоянными коэффициентами.
5.Уравнения гиперболического, параболического и эллиптического типов. Уравнение Трикоми.
6.Замена независимых переменных.
7.Каноническая форма уравнения.
8.Характеристическое уравнение. Характеристики.
9.Канонические виды уравнений гиперболического, параболического и эллиптического типов. Канонические виды линейных уравнений с постоянными коэффициентами гиперболического, параболического и эллиптического типов.
10.Классификация квазилинейных дифференциальных уравнений второго порядка со многими переменными в точке.
11.Канонический вид квазилинейного дифференциального уравнения с постоянными коэффициентами со многими переменными в точке.
12.Канонические виды линейных дифференциальных уравнения второго порядка гиперболического, параболиче-
32

ского и эллиптического типов с постоянными коэффициентами с тремя и четырьмя переменными.
13.Характеристическая поверхность (характеристика) квазилиейного дифференциального уравнения. Характеристическое уравнение. Характеристическая линия.
14.Характеристический конус. Конусы будущего и прошлого.
15.Характеристики уравнения теплопроводности.
Задачи для самостоятельного решения
Привести к канонической форме уравнения 1 и 2.
1. |
z |
4z |
3z |
2z |
6z |
0. |
|
xx |
xy |
yy |
x |
y |
|
2. |
|
|
|
0. |
zxx |
2zxy |
2zyy |
3. Преобразовать уравнение
u |
yu |
|
1 |
u |
0 |
|
|||||
xx |
yy |
|
2 |
y |
|
|
|
|
|
|
к кано-
ническому виду в области, в которой оно принадлежит к гиперболическому классу.
4. Преобразовать к каноническому виду уравнение с по-
|
|
|
|
|
|
u 0. |
стоянными коэффициентами auxx 2auxy |
auyy |
cuy |
||||
|
5. В |
области эллиптичности |
привести |
уравнение |
||
|
|
0 к канонической форме. |
|
|
|
|
uxx |
xyuyy |
|
|
|
|
|
33
ГЛАВА 3. КРАЕВЫЕ ЗАДАЧИ МАТЕМАТИЧЕСКОЙ ФИЗИКИ
3.1. Постановка краевых задач для уравнений математической физики
Классификация краевых задач.
Пусть G – область, где происходит физический процесс, и S – еѐ граница. С целью полной интерпретации того или другого физического явления, нужно, помимо уравнения, моделирующего данное явление, закрепить начальное состояние данного явления (начальные условия) и режим на границе области, где осуществляется данное явление (граничные условия). Начальные и граничные условия именуются краевыми условиями. Соответствующая задача для дифференциального уравнения именуется краевой задачей. Классифицируют такие три основных вида краевых задач для дифференциального уравнения.
а) Задача Коши для уравнений гиперболического и параболического классов: имеются начальные условия, граничных условий нет.
б) Краевая задача для уравнений эллиптического класса: присутствуют граничные условия на границе S, началь-
ных условий нет.
в) Смешанная задача для уравнений гиперболического и параболического классов: имеются и начальные, и граничные условия.
Корректность в постановке задач математической физики.
Поскольку задачи математической физики являются математическими моделями действительных физических явлений, то для их постановок обязательно выполнение нижеперечисленных условий.
а) Решение должно существовать.
34

б) Решение должно быть единственным.
в) Решение должно непрерывно зависеть от данных за-
дачи (начальных и граничных данных, свободного члена, коэффициентов уравнения и так далее), что означает его устойчивость к незначительным отклонениям исходных данных.
Задача, для которой выполняются эти условия, именуется корректно поставленной (по Адамару). Задача, для которй не выполняется, по крайней мере, одно из требований а) – в),
именуется некорректно поставленной.
Устойчивость решения к незначительным отклонениям исходных данных для корректности задачи по Адамару трактуется в том смысле, что в данной задаче незначительные отклонения начального состояния могут вызывать только малые отклонения очередных состояний, то есть если
u1 0 u2 |
0 , то |
u1 t u2 t K |
для всех t 0, t0 . |
|
Здесь |
K |
– некоторая постоянная. |
|
|
|
Условие устойчивости решения отвечает простому фак- |
|||
ту, что определению начального состояния системы обязательно сопутствует процесс измерения, обладающий определѐнной погрешностью. Следовательно, физически разумной нужно считать постановку задачи, при которой незначительная погрешность в определении начального состояния системы не приводит к значительным ошибкам в прогнозировании очередных состояний.
К некорректно поставленным задачам математической физики часто приводят обратные задачи нахождения характеристик процессов по результам измерений. Таковыми обратными задачами являются задача нахождения теплофизических характеристик материала по итогам оределения температуры в некоторых точках и гравиметрическая задача нахождения вида и размера аномалии плотности по данным измерения силы тяжести на поверхности Земли.
35

3.2.Задачи на бесконечной прямой. Задача Коши. Уравнение колебаний струны и его решение
методом Даламбера
Исследуем свободные колебания бесконечной струны, то есть достаточно длинной струны, влияние концов которой на процесс колебаний можно не учитывать.
Причинами таких возмущений возможны начальные отклонения струны от положения равновесия или приданный струне начальный импульс, вызывающий определѐнное распределение скоростей частиц струны. Следовательно, моделируя свободные колебания бесконечной струны, требуется найти решение однородного уравнения свободных колебаний
|
u |
|
|
|
u |
|
|
2 |
|
a |
|
2 |
|
|
, |
t |
|
2 |
x |
|
|||
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
||
с начальными условиями
u |
t 0 |
x |
|
|
|
|
|
здесь функции x |
и |
||
оси.
Начальные условия
t
;
0, x , |
36 |
|||||
|
|
|
||||
u |
|
x , |
|
|
|
|
t |
t 0 |
37 |
||||
|
||||||
|
|
|
|
|||
|
|
|
|
|
||
x |
определены всюду на числовой |
|||||
37 |
единственным образом задают |
|||||
возмущения бесконечной струны. В этом случае задача |
36 , |
37 |
именуется задачей с начальными условиями или задачей |
||||||||||||||||||
Коши. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решим данную задачу методом Даламбера. С этой це- |
||||||||||||||||||
лью |
зададим |
новые |
независимые |
|
аргументы |
x at; |
|||||||||||||
x at. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Находя производные в новых аргументах, получим: |
||||||||||||||||||
u u u au au |
a |
u |
u |
|
; |
|
|
|
|
||||||||||
t |
|
t |
t |
|
|
|
|
|
|
|
|
|
2u |
u |
|
; |
|||
u a u u u u |
|
a |
|
|
u |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
tt |
|
t |
t |
|
t |
|
t |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
36 |
|
|
|
|
|
|
|
|
|
|
||
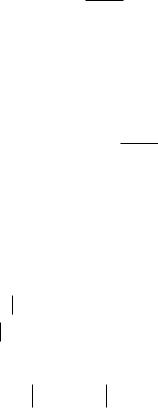
u u u |
u u |
; |
|||
t |
x |
x |
|
|
|
u |
u |
u |
u |
u |
u |
2u |
u . |
||
xx |
|
x |
x |
|
x |
x |
|
|
|
|
Уравнение |
36 |
с новыми аргументами примет |
||||||
такого дифференциального уравнения для функции u
форму
, :
a |
|
|
u |
2u |
u |
a |
|
u |
|
2u |
u |
; |
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
u |
|
|
|
|
|
||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0. |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||
4u |
0 |
|
|
или
Непосредственной подстановкой можно проверить, что решением уравнения является функция типа
где
u |
|
1 |
|
и
u |
2 |
|
|
|
u , u1 u2 ,
– произвольные дважды дифференцируе-
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 |
|
|
|
u2 |
|
|
|
|
мые функции. Действительно, |
|
|
|
|
|
0. |
||||
|
|
|
|
|
|
|
|
|
||
тельно, функция |
|
|
|
|
|
|
|
|
|
|
u x, t u |
x at |
u |
x at , |
|
|
|
|
|||
1 |
|
2 |
|
|
|
|
|
|
|
|
удовлетворяет уравнению 36 .
Следова-
38
Определим теперь u1 и |
u2 таким образом, |
||||||||
влетворялись начальные условия 37 . Тогда |
|
|
|||||||
|
u |
t 0 |
u |
x u |
x x , |
|
|
||
|
|
|
1 |
2 |
|
|
|
||
u |
t 0 |
au x au x x . |
|
|
|||||
|
|
|
|
1 |
2 |
|
|
||
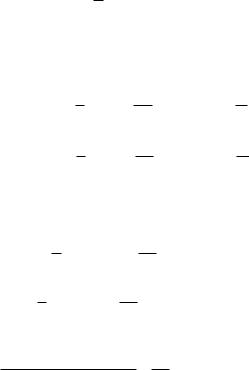
Интегрируя равенство |
40 в пределах от x0 |
до |
x, |
||||||
|
|
|
|
|
|
|
x |
|
|
au2 x xx0 |
au1 x |
xx0 d |
|
|
|||||
|
|
|
|
|
|
|
x0 |
|
|
чтобы удо-
3940
получаем
или
37
|
|
|
|
|
|
|
1 |
x |
|
d С, |
|
||||||
|
|
u |
2 |
|
1 |
|
|
|
|||||||||
|
|
|
x u x |
a |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
где |
x0 и С |
– постоянные, |
С u2 |
x0 |
u1 |
x0 . |
|
||||||||||
|
Из системы уравнений |
39 |
и |
41 |
имеем |
|
|||||||||||
|
|
|
|
|
x |
|
1 |
x |
1 |
x |
d |
С |
|||||
|
|
|
|
u |
|
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
1 |
|
|
2 |
|
|
|
|
|
2a |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
x |
|
|
С |
|
|
|
|
u2 |
x |
x |
d |
||||||||||
|
|
|
|
2 |
2a |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
Подставляя теперь функции u1 и u2 в уравнение дим
|
|
1 |
|
|
1 |
x at |
|
u x, t |
x at |
d |
|||||
2 |
2a |
||||||
|
|
|
|
x |
|||
|
|
|
|
|
|
0 |
|
|
1 |
|
|
1 |
x at |
|
|
|
x at |
d , |
|||||
2 |
2a |
||||||
|
|
|
x |
|
|||
|
|
|
|
|
0 |
|
|
;
.
38 ,
41
нахо-
или
u x, t |
x at |
|
|
|
|
Если функция |
|
|
2x
x at |
|
1 |
x at |
d . |
|
|
|
|
42 |
||||
|
2a |
|||||
|
|
x at |
|
|||
|
|
|
|
|||
|
|
|
|
|
имеет производные первого и вто-
рого порядка включительно, а функция x – первого порядка, то соотношение 42 является решением задачи Коши36 , 37 . В этом случае ение 42 именуется формулой Даламбера. Из неѐ вытекает, что для задачи Коши 36 , 37
волнового уравнения существует только одно решение, непрерывно зависящее от начальных условий, то есть если
 1 x 2 x
1 x 2 x  1 и
1 и  1 x 2 x
1 x 2 x  2 , то
2 , то
38
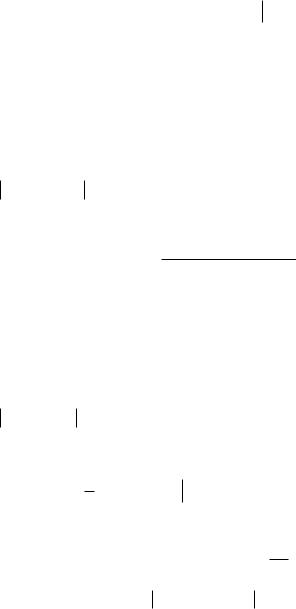
и |
|
0,
когда
1, 2
 u1 0.
u1 0.
x, t u |
2 |
x, t , |
Данное свойство непрерывной зави-
симости решения от начальных условий гарантирует корректность постановки задачи Коши для уравнения гиперболического класса, являющуюся следствием физической детерминированности моделируемого волнового явления.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
u |
|
|
2 |
u |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Пример 1. Найти решение уравнения |
t |
2 |
|
x |
2 |
|
, |
если |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u |
t 0 |
|
x2 , |
u |
t 0 |
|
0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Решение. Так как a 1, а |
x 0, |
|
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
u |
x at x at |
, |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
2 |
. Таким образом, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x at |
2 |
x at |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
u |
|
|
x |
2 |
t |
2 |
. |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
u |
|
|
|
u |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
||
|
|
|
Пример 2. Найти решение уравнения |
t |
2 |
4 |
x |
2 |
, если |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
u |
|
|
0, |
u |
|
|
x. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
t 0 |
|
t |
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Здесь a 2, |
x 0, |
|
x x. Отсюда |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
x 2t |
|
|
2 |
|
|
x |
2t |
2 |
x 2t |
2 |
|
|
|
|
|
||||||||||||
|
|
|
|
|
u |
|
|
|
d |
|
x 2t |
|
|
|
|
xt. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
x 2t |
|
8 |
|
|
|
|
|
|
|
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Пример 3. Определить вид струны, задаваемой уравне- |
||||||||||||||||||||||||||||||||
|
|
|
|
u |
|
|
|
u |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
нием |
|
|
a |
2 |
|
|
|
|
в момент времени t |
|
|
|
|
при условии, что |
|||||||||||||||||||||
t |
2 |
|
x |
2 |
2a |
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
u t 0 sin x, |
u |
|
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
t |
|
t 0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
39 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

Решение. Имеем
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
sin x |
|
|
1 |
x |
2 |
|
|
|
u |
|
2 |
|
2 |
|
|
d |
, |
|||
|
|
2 |
|
2a |
2a |
||||||
|
|
|
|
|
x |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
2 |
|
|
|
то есть струна параллельна оси абсцисс.
Неоднородное уравнение.
Вынужденные колебания бесконечной струны описы-
ваютя уравнением
|
u |
|
|
|
u |
|
|
2 |
|
a |
|
2 |
|
|
g x, t , x , 0 t . |
t |
|
2 |
x |
|
|||
2 |
|
|
2 |
|
|||
|
|
|
|
|
|
||
Пусть требуется найти решение этого уравнения, удовлетворяющего начальным условиям (решить задачу Коши):
u |
|
0 |
|
f |
x , |
|
|
|
|
t |
|
1 |
|
43 |
|
|
|
|
|
||||
|
u |
|
|
x . |
|||
f2 |
|
||||||
|
t |
|
|||||
|
|
|
|
|
|
||
Решение исходной задачи ищут в виде:
|
u x, t v x, t w x, t , |
здесь функция |
v x, t представляет собой частное решение |
однородного дифференциального начальными условиями, а функция
уравнения с исходными
w x, t |
– неоднородного |
дифференциального уравнения с нулевыми начальными условиями:
|
|
v |
|
|
|
|
|
v |
|
|
|
|
|
w |
|
|
|
|
|
|
w |
|
|||||
|
|
2 |
2 |
a |
|
|
2 |
2 |
, |
|
|
|
2 |
|
2 |
|
a |
|
|
2 |
|
2 |
g x, t , |
||||
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
t |
|
|
|
|
x |
|
|
|
|
|
t |
|
|
|
|
|
x |
|
|
||||||
1) |
|
|
|
f1 |
x , |
|
2) |
|
|
|
|
|
0, |
|
|
|
|
|
|||||||||
v t 0 |
|
w t 0 |
|
|
|
|
|
||||||||||||||||||||
|
|
v |
|
|
|
|
|
x |
; |
|
|
w |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
f |
|
|
|
|
|
0. |
|
|
|
|
|||||||||||||
|
t |
t |
0 |
2 |
|
t |
|
t 0 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение первой задачи даѐтся формулой Даламбера:
40
