2568

Используя константы подобия, выражаем величины 2-й системы через величины 1-й системы:

С помощью последних соотношений переменные 2-й системы заменя-

ем через переменные 1-й системы и константы подобия:

Полученное соотношение разделим на уравнение 1-й системы, что дает

(21)

Таким образом, получили выражение, составленное лишь из констант подобия. Выражение типа (21) называется индикатором подобия, который всегда равен единице. Индикатор подобия накладывает ограничения на вы-

бор констант подобия. В рассмотренных двух подобных явлениях три кон-

станты подобия можно выбрать произвольно, а четвертая определяется из индикатора подобия (13.21).

6. Заменяя в индикаторе подобия константы подобия отношением од-

нородных величин, получаем безразмерный комплекс, называемый критери-

ем или числом подобия, который для всех подобных явлений сохраняет одно и то же численное значение:

(22)

Теория подобия базируется на трех теоремах подобия. Первая теорема подобия: подобные между собой явления имеют одинаковые числа подобия.

Первая теорема подобия дает возможность получить числа подобия из дифференциальных уравнений, не прибегая к их интегрированию. Для этого дифференциальные уравнения должны быть подвергнуты преобразованиям подобия, последовательность которых включает следующие операции:

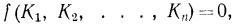
а) на основании математического описания двух подобных явлений выявляют переменные величины и составляют на их основе константы подо-

бия;

б) входящие в уравнения переменные величины 2-й системы выражают через однородные величины 1-й системы и константы подобия;

в) в преобразованных таким образом уравнениях 2-й системы группи-

руют члены так, чтобы из констант подобия были составлены индикаторы подобия;

г) константы подобия, входящие в полученные индикаторы подобия,

заменяют отношениями однородных величин и получают числа подобия.

Вторая теорема подобия: интеграл дифференциального уравнения мо-

жет быть представлен в виде функции от чисел подобия этого дифференци-

ального уравнения:

(23)

где Ki - число подобия.

Уравнение типа (23) называется критериальным уравнением.

Помимо чисел подобия, в критериальное уравнение могут входить так называемые симплексы - безразмерные отношения однородных величин.

Вторая теорема подобия не устанавливает конкретный вид функции f в

(23), однако она указывает, как должны обрабатываться опытные данные и результаты численного расчета - в виде критериальных уравнений. Критери-

альные уравнения, составленные на основе второй теоремы, справедливы для всех подобных между собой явлений. Вторая теорема позволяет значительно сократить число переменных, тем самым облегчая получение расчетных за-

висимостей и сокращая объем экспериментов и численных расчетов.

Третья теорема подобия: подобны те явления, математическое описа-

ние которых совпадает по форме и по существу, условия однозначности ко-

торых подобны и критерии (числа подобия), составленные из условий одно-

значности, численно одинаковы.

Третья теорема подобия позволяет выявить группу подобных явлений,

на которую можно распространить критериальное уравнение, полученное на основе численных расчетов или эксперимента. На основе третьей теоремы подобия создан метод моделирования натурных процессов,

1.6. Критериальные уравнения и числа подобия конвективного тепло-

обмена Пусть имеются два подобных явления конвективного теплообмена, ко-

торые описываются следующей системой уравнений:

(24)

(25)

(26)

с граничным условием для теплообмена

(27)

Обозначим переменные первого явления индексом ( ), второго явления

- индексом ( ).

Поскольку конвективный теплообмен связан с движением жидкости,

рассмотрим вначале гидродинамическое подобие, определяющее условия,

при которых в геометрически подобных системах осуществляются подобные течения. Подвергнем уравнение движения (24) подобным преобразованиям.

1. Запишем константы подобия по формуле (13.20)

(28)

где h и l геометрические размеры тела.

2. Выразим переменные второго явления через одноименные величины первого явления и константы подобия:

(29)

3. Для тождественности уравнений движения обоих явлений необхо-

димо, чтобы комплексы, составленные из констант подобия, сократились, что позволяет записать

Сгруппируем константы подобия таким образом, чтобы из них получи-

лись индикаторы подобия. Для этого рассмотрим члены последнего соотно-

шения попарно, что дает:

4. Константы подобия, входящие в индикаторы подобия, заменим с по-

мощью (28) отношениями переменных величин и получим числа подобия:

или

(29)

При гидродинамическом подобии двух или нескольких явлений для любых сходственных точек числа подобия Eu, Fr и Re имеют одни и те же численные значения. Из геометрического подобия систем получаем симплекс

l/h. Легко показать, что подобие уравнений неразрывности (25) выполняется автоматически как следствие гидродинамического подобия.

Искомой величиной при решении или исследовании гидродинамики является перепад давления. Перепад давления входит в число Эйлера. Такое число подобия, в которое входит искомая величина, называется определяе-

мым. Остальные числа подобия и симплексы (Fr, Re, l/h) - определяющие.

Следовательно, критериальное уравнение гидродинамики имеет вид

Число Эйлера при течении в трубах связано с коэффициентом сопро-

тивления Сf=2Еu, где

(30)

Тепловое подобие определяет условия, при которых в геометрически и гидродинамически подобных системах осуществляется подобие температур-

ных полей и тепловых потоков.

Подвергнем преобразованиям подобия уравнение энергии (26) с гра-

ничным условием (27), для чего введем в дополнение к константам подобия

(28) новые константы подобия:

(31)

Повторяя аналогичные операции, какие проводились с уравнениями количества движения, получим из (26):

и из граничного условия (13.27):

откуда имеем индикаторы подобия:

Заменяя константы подобия отношением однородных величин, получа-

ем два новых числа подобия:

(32)

(33)

При исследовании Конвективного теплообмена искомой величиной яв-

ляется коэффициент теплоотдачи , который входит в число Нуссельта. Сле-

довательно, число Нуссельта - определяемый критерий для процессов Кон-

вективного теплообмена.

Таким образом, с учетом гидродинамического и геометрического по-

добия получаем критериальное уравнение Конвективного теплообмена:

(34)

где h и l - характерные размеры тела.

Если критерий Нуссельта (33) умножить и разделить на разность тем-

ператур T, то будем иметь:

Следовательно, критерий, или число, Нуссельта характеризует соотно-

шение между Конвективным переносом теплоты от жидкости к стенке qкон и

переносом теплоты теплопроводностью qтеп через слой жидкости толщиной l.

Иногда вместо числа Нуссельта используется число Стен-тона, пред-

ставляющее собой комбинацию чисел подобия Nu, Re и Рr:

Из этой зависимости следует, что

Следовательно, число Стентона - отношение теплового потока, посту-

пающего в стенку, к конвективному потоку, который может быть перенесен потоком жидкости при уменьшении ее температуры от Ts до Тw

Число Рейнольдса выражает соотношение между инерционной силой и силой внутреннего трения, в чем нетрудно убедиться, если умножить и раз-

делить формулу (29) на скорость .

Число Фруда характеризует соотношение работы сил гравитации к ки-

нетической энергии потока:

Комбинация чисел Фруда и Рейнольдса дает новый Критерий - число Галилея:

При свободном движении, обусловленном неоднородностью поля плотности, число Галилея следует умножить на симплекс / , что дает чис-

ло Архимеда:

Если разность плотностей жидкости зависит только от разности темпе-

ратур, то / =Т, где - термический коэффициент объемного расшире-

ния:

Для газов =1/T. Тогда число Архимеда можно преобразовать в

который называется числом Грасгофа и характеризует соотношение между подъемной силой и силой вязкости.

Используя выражение для коэффициента температуропроводности

= /с , можно число Пекле записать в виде

Число Пекле характеризует изменение энтальпии потока к количеству теплоты, переданной теплопроводностью. Умножая и деля число Ре на кине-

матическую вязкость, получим

Отношение v/a называется числом Прандтля:

(36)

в которое входят только физические параметры жидкости.

Для газов число Прандтля не зависит ни от температуры, ни от давле-

ния. Величина его определяется атомностью газа, и чем выше атомность, тем больше число Рr приближается к единице. Для двухатомных газов (воздух)

Рr=0,72. Для капельных жидкостей число Рr больше единицы.

Как увидим дальше, число Прандтля пропорционально отношению толщины динамического пограничного слоя к толщине теплового слоя T

С введением новых критериев критериальное уравнение (34) Конвек-

тивного теплообмена записывается в виде

(37)

Для предельных случаев Конвективного теплообмена критериальное уравнение (37) упрощается. В случае вынужденной конвекции из (37) может быть опущено число Gr:

(38)

В случае естественной конвекции из (37) исчезает число Re:

(39)

Заметим, что в случае естественной конвекции в критериальное урав-

нение (39) входит произведение GrPr, называемое числом Релея Re.

При смешанной конвекции критериальное уравнение будет содержать отношение Gr/Re2:

(40)

Критерии, входящие в критериальные уравнения конвективного тепло-

обмена, содержат физические параметры жидкости ( , a, v, с, и т. д.), кото-

рые являются функциями температуры.

Температура, при которой выбираются физические параметры жидко-

сти, называется определяющей температурой. Такой температурой могут быть: температура пограничного слоя Тт=(Ts+Tw)/2, средняя температура жидкости Ts, средняя температура поверхности твердого тела Tw. Обычно критериальные уравнения снабжаются индексами, указывающими, при какой температуре следует выбирать физические параметры жидкости.

Числа Nu, Re и Gr содержат геометрический размер тела, поэтому при построении критериальной зависимости указывают, какой из геометрических размеров тела входит в эти числа. Такой геометрический размер называют определяющим. Например, для трубы или шара определяющим размером яв-

ляется их диаметр, для плиты - ее длина. Для каналов сложного сечения в ка-

честве определяющего размера берется эквивалентный диаметр

где F - площадь поперечного сечения канала; Р - периметр поперечного сечения.

Критериальное уравнение теплопроводности твердых тел, не содержа-

щих внутренних источников теплоты, имеет вид

(42)

где Т - безразмерная температура.

Числа подобия, входящие в правую часть уравнения (42), называются:

Число Фурье - безразмерное время, а число Био - соотношение между количеством теплоты, подведенной за счет конвекции к поверхности тела, и

теплоты, отведенной в твердом теле за счет теплопроводности. Число Био формально аналогично числу Нуссельта, однако принципиальное отличие состоит в том, что в число Био входит коэффициент теплопроводности твер-

дого тела, а в число Нуссельта - коэффициент теплопроводности жидкости.

Обычно конкретный вид критериального уравнения представляют в виде степенной функции от определяющих критериев подобия. Например,

для теплообмена при вынужденной конвекции на непроницаемой стенке конкретный вид критериального уравнения (38) может быть записан как

где показатели степеней т, п и k, а также постоянная находятся из экс-

периментов или численных расчетов.

1.7. Гидродинамическая аналогия конвективного теплообмена (Анало-

гия Реинольдса)

Гидродинамическая аналогия определяет условия, при которых имеет место аналогия между полем скорости и полем температуры, и устанавливает аналитическую связь между безразмерным коэффициентом трения и безраз-

мерным коэффициентом теплоотдачи.