2568

Пусть твердое тело омывается потенциальным потоком со скоростью

Us(x) (рис. 3). Поскольку мы рассматриваем тонкий пограничный слой, мож-

но предположить, что толщина этого слоя очень мала по сравнению с лю-

бым размером тела, погруженного в поток и окруженного пограничным сло-

ем, т. е. можно принять, что толщина пограничного слоя имеет малый поря-

док .

Если поверхность тела искривлена и пограничный слой также тонок

по сравнению с радиусом кривизны, то при этих условиях можно выбрать систему координат, как показано на рис.3, на которой ось х направлена вдоль поверхности, а ось y - по нормали к ней. Поскольку внутри пограничного

слоя координата у изменяется от 0 до , то порядок у есть также , т.е. 0(y)=

, а порядок продольной координаты х можно принять близким к размеру те-

ла и положить 0(x)=1.

Скорость потенциального течения Us, а также продольную скорость в пограничном слое u и плотность примем порядка единицы:

0(Us)=1; 0(u)=1; 0( )=1.

Проанализируем уравнения Навье-Стокса (6) и (7), а также уравнение неразрывности (8) с позиций отмеченных выше основных положений теории

пограничного слоя для вынужденного течения ( g=0).

Из уравнения неразрывности (8) можно легко определить порядок по-

перечной скорости v. Это уравнение требует, чтобы оба его члена имели одинаковый порядок. Поскольку u и х порядка единицы, производная du/dx

должна быть такого же порядка. Следовательно, порядок второго члена так-

же равен единице, т. е. 0(dv/dy)=1. Но 0(у)= , тогда 0(v)= :

Порядок продольного градиента давления / x определяется из уравнения Бернулли (9), справедливого для потока вне пограничного слоя

(y> ), где жидкость можно считать идеальной ( =0):

(9)

В уравнении (9) первый член, выражающий инерцию, имеет порядок единицы, и тогда член с продольным градиентом давления имеет также по-

рядок единицы 0(/ x) 1.

Перейдем теперь к оценке членов уравнения движения в направлении продольной координаты х:

Левая часть уравнения имеет порядок единицы. В правой части первый член также порядка единицы. В круглых скобках правой части можно пре-

небречь первым членом 2u/ х2 по сравнению с членом 2u/ у2. Согласно оп-

ределению в динамическом пограничном слое инерционные силы и силы вязкости имеют одинаковый порядок. Для сохранения в уравнении члена с

но, если положить вязкость порядка 2, т.е. 0( )= 2. Это означает, что поток типа пограничного слоя будет иметь место, если вязкость жидкости ничтож-

но мала.

Порядок оценки членов уравнения движения в проекции на ось у при-

водит к

Все члены уравнения имеют порядок величины . Следовательно, / у

должно быть порядка , которым можно пренебречь по сравнению с величи-

нами порядка единицы в уравнении движения в направлении х. Порядок

0(/ у)=указывает, что изменение давления по направлению к нормали пренебрежимо мало. Другими словами, давление в пограничном слое опре-

деляется внешним потенциальным потоком. Система уравнений, описываю-

щих стационарный двумерный вынужденный поток жидкости с постоянны-

ми характеристиками в пограничном слое, имеет вид:

(10)

(11)

(12)

Граничные условия для непроницаемой стенки формулируются как:

при у=0, u=0, v=0; при yu=us. Может показаться странным, что второе граничное условие записано для y , тогда как система уравнений погра-

ничного слоя описывает поток в тонком пристенном слое. Решения, полу-

ченные из этих уравнений, показывают, что скорость потока быстро прибли-

жается на близком расстоянии от стенки к постоянной величине, равной ско-

рости Us потенциального потока.

Уравнения движения пограничного слоя также нелинейные; однако они существенно проще, чем уравнения Навье-Стокса, поскольку в них от-

сутствует второе уравнение движения, давление теперь следует рассматри-

вать как величину, определяемую потенциальным течением. Кроме того,

один из двух членов вязкости в оставшемся уравнении движения также опу-

щен.

Для симметричного вращательного потока уравнение движения (10)

одинаково с уравнением для плоского течения. Единственное изменение имеет место в уравнении неразрывности, которое приобретает вид

(13)

где r - расстояние рассматриваемой точки от оси вращения.

Если температура поверхности тела T , отличается от температуры по-

тока Ts, то вблизи поверхности тела образуется тепловой пограничный слой толщиной т (см. рис.3).

Образование теплового пограничного слоя, толщина которого в общем случае отлична от толщины динамического слоя ( т), связано с торможе-

нием жидкости у поверхности тела, что в свою очередь обусловливает оди-

наковый порядок величин переноса теплоты за счет конвекции и молекуляр-

ной теплопроводности.

Следовательно, тепловым пограничным слоем называется тонкий слой жидкости у поверхности тела, в котором молекулярная теплопроводность одинакового порядка с конвективным переносом теплоты и в котором попе-

рек этого слоя наблюдаются существенные градиенты температуры.

Проанализируем уравнение энергии с позиций теории пограничного слоя для условий, оговоренных в п.2. Положим, что порядок величины тем-

пературы равен единице: 0(Т)=1. Тогда оценка порядка членов уравнения энергии дает

Левая часть уравнения имеет порядок единицы. В правой части член

2Т/ x2 порядка единицы и пренебрежимо мал по сравнению с членом

2Т/ y2, имеющим порядок 1/ 2.

Для сохранения члена с теплопроводностью необходимо, чтобы член

a 2T был порядка единицы, что будет выполнено, если положить темпера-

y 2

туропроводность порядка 2, т.е. 0(а)= 2. Окончательно уравнение энергии пограничного слоя упрощается и имеет вид

(14)

1.4. Интегральные соотношения пограничного слоя Полный расчет пограничного слоя путем решения дифференциальных

уравнений пограничного слоя требует много времени, сопряжен со значи-

тельными усилиями и может быть выполнен при фундаментальной матема-

тической подготовке. Поэтому для студентов и инженеров с математической подготовкой технических вузов это практически недоступно и возникает не-

обходимость использования в инженерной практике приближенных методов,

иногда даже в ущерб точности решения.

Одним из наиболее распространенных методов приближенного реше-

ния уравнений пограничного слоя для получения его интегральных характе-

ристик (коэффициентов трения, теплообмена и массообмена) является метод,

основанный на использовании интегральных соотношений пограничного слоя.

Интегральные соотношения получаются интегрированием дифферен-

циальных уравнений пограничного слоя но поперечной координате у в пре-

делах от 0 (поверхность твердого тела) до расстояния h, при котором про-

дольная скорость становится равной скорости потенциального течения

(u=us), а температура - равной температуре внешнего потока (T=Ts).

Прежде чем интегрировать дифференциальные уравнения погранично-

го слоя, в них поперечную составляющую скорости v выражают через про-

дольную составляющую и, используя для этой цели уравнение неразрывно-

сти (12), что дает

интегральное соотношение количества движения, или соотношение Кармана,

для непроницаемой поверхности при вынужденном течении n условий, ого-

воренных в п.2, имеет вид

(15)

где - касательное напряжение на поверхности твердого тела для ла-

минарного пограничного слоя оно определяется законом трения Ньютона производная dus/dx характеризует величину продольного градиента давления.

Интегральное соотношение энергии (уравнение Г. H. Кружилина) для непроницаемой поверхности выражается уравнением

(16)

где qw - тепловой поток на поверхности твердого тела, который для ла-

минарного течения определяется законом Фурье.

Интегральные соотношения (15) и (16) являются такими же строгими в рамках допущений теории пограничного слоя, как и дифференциальные уравнения пограничного слоя. Преимущество интегральных соотношений заключается в том, что они позволяют легко получать приближенные реше-

ния.

Метод приближенного решения интегральных соотношений был пред-

ложен Т. Карманом и Е. Польгаузеном. Этот метод основан на двух основ-

ных допущениях: 1) верхний для асимптотического пограничного слоя бес-

конечный предел интегрирования заменяется конечным пределом интегри-

рования, равным [для уравнения (15) и т для уравнения (16)], на расстоя-

нии которых продольная скорость и температура пограничного слоя прини-

маются равными скорости Us и температуре Ts потенциального течения; 2)

произвольные выражения для распределений скорости и температуры внутри пограничного слоя с некоторым числом постоянных, вычисляемых с соблю-

дением определенных условий.

Наиболее распространенным способом задания распределений скоро-

сти и температуры в пограничном слое является их задание в виде полино-

мов:

(17)

(18)

где коэффициенты аi и bi являются функциями продольной координаты х и

находятся из граничных условий.

Следует заметить, что во всех случаях разумного применения этого приближенного метода он давал удовлетворительные результаты.

1.5. Основы теории подобия Анализ системы уравнений конвективного теплообмена показывает,

что температурное поле и градиент температуры, а следовательно, и коэффи-

циент теплоотдачи а даже для простейших случаев зависят от многих факто-

ров:

где в дополнение к известным факторам введено: l1,l2 - размеры и Ф -

форма тела.

Для нахождения конкретного вида функции f (в 19) могут быть исполь-

зованы три метода: 1) аналитическое решение дифференциальных уравнений и интегральных соотношений пограничного слоя; 2) численный расчет диф-

ференциальных уравнений на ЭВМ; 3) экспериментальное изучение кон-

кретного случая теплообмена.

Во всех случаях, когда это возможно, следует использовать аналитиче-

ский метод даже в приближенной постановке на основе интегральных соот-

ношений пограничного слоя, поскольку аналитический метод позволяет по-

лучить расчетную формулу, описывающую целый класс задач Конвективно-

го теплообмена.

Численный расчет дифференциальных уравнений расширяет круг за-

дач, которые могут быть вычислены на ЭВМ, по сравнению с аналитическим методом.

Экспериментальное изучение позволяет с той или иной степенью точ-

ности решать практически любые задачи конвективного теплообмена. Одна-

ко два последних, по существу, равноценных метода обладают весьма суще-

ственным недостатком: результат конкретного численного решения или экс-

перимента, в итоге которых получается одно численное значение искомой величины - коэффициента теплоотдачи, обладает ограниченной ценностью.

А именно, этот результат не может быть распространен на другую задачу или явление, которое чем-то отличается от изученного. Чтобы найти зависимость коэффициента теплоотдачи хотя бы от одного из аргументов, необходимо выполнить большое количество численных решений или экспериментов. А

для количества аргументов, входящих в (19), это вообще практически невы-

полнимая задача. Эти трудности, возникающие при численных расчетах и экспериментальном изучении задач конвективного теплообмена, позволяет преодолеть теория подобия.

Большой вклад в развитие теории подобия внесли советские ученые М.

В. Кирпичев, А. А. Гухман, М. А. Михеев, Л. И. Седов и др.

Теория подобия устанавливает: 1) условия подобия физических явле-

ний; 2) правила объединения физических величин, от которых зависит дан-

ное явление, в безразмерные комплексы, составленные из этих величин; чис-

ло безразмерных комплексов существенно меньше числа физических вели-

чин, что позволяет значительно сократить число экспериментов и численных расчетов и облегчает их обобщение; 3) правила моделирования процессов,

протекающих в натурных условиях.

В теории подобия безразмерные комплексы, объединяющие физиче-

ские величины, получаются на основе анализа дифференциальных уравне-

ний, описывающих явления и содержащих общие связи этих величин.

Познакомимся вначале с основными определениями и особенностями подобных явлений.

1.Понятие подобия в отношении физических явлений применимо лишь

кявлениям одного и того же рода, описываемых формально и по существу одними и теми же уравнениями.

2.Подобные явления протекают в геометрически подобных системах.

3.При анализе подобных явлений сравнивать между собой можно лишь однородные величины в сходственных точках и в сходственные момен-

ты времени.

Однородными называют величины, имеющие один и тот же физиче-

ский смысл и одинаковую размерность.

Сходственными называют такие точки, координаты которых удовле-

творяют условию

где С - постоянная величина, одинаковая для всех точек пространства.

Сходственными моментами времени называют такие, для которых справедливо равенство

где С- постоянная величина для любого момента времени.

4. Подобие двух физических явлений означает подобие всех величин,

характеризующих явления, т. е. в сходственных точках пространства и в

сходственные моменты времени любая величина 2 второго явления пропор-

циональна однородной с ней величине 1 первого явления:

станту подобия, численно отличную от других, т. д. Ст С С . Свойство (20)

констант подобия ограничено только одинаковой размерностью.

5. Для сложных процессов, характеризующихся многими величинами,

константы подобия этих величин находятся между собой в определенной связи, и их нельзя выбирать произвольно. Поясним это положение на про-

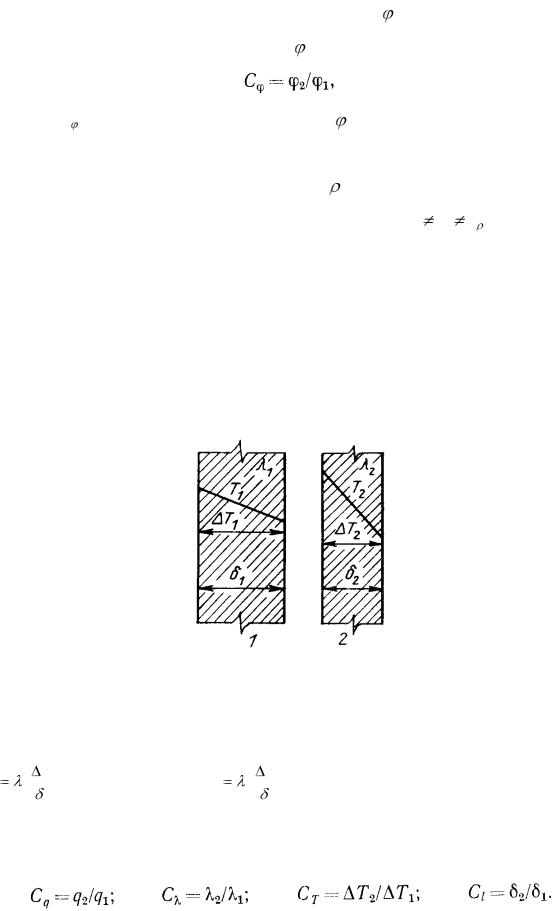
стом примере стационарной передачи теплоты теплопроводностью через плоскую стенку (рис.4).

Рис. 4. К определению свойств подобных явлений Имеются две плоские стенки разной толщины и из разных материалов. Коли-

чество теплоты, которое передается теплопроводностью через стенку1, равно

место геометрическое подобие и явления описываются одними и теми же уравнениями. По формуле (20) находим константы подобия: