Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

2536

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.8 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

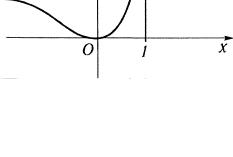
Находим предел lim	x2	= ∞, т. е. прямая х = 1 есть
Находим предел lim	(x −1)2	= ∞, т. е. прямая х = 1 есть
x→1	(x −1)2
вертикальная асимптота. При x → ±∞			предел lim	x2		=1 ,
вертикальная асимптота. При x → ±∞			предел lim		2	=1 ,
			x→±∞ (x −1)		2

т. е. прямая у = 1 есть горизонтальная асимптота. График функции показан на рис. 2.62.

						Рис. 2.62
14.2. Исследовать функции и построить их графики:
а)	x = a cos3 t,				y = a sin 3 t, t [0,2π[; ;
б)	x = a(t −sin t),					y = a(1 − cos t), t [0,2π] ;
в)	x =	3at		,	y =	3at 2	.
		1 +t	3			1 +t 3

Решение. a) Функции определены для любого значения t. Поскольку функция x четная, а у нечетная, то график функции симметричен относительно оси ординат и начала координат, т.е. относительно координатных осей.

Полагая x = 0, находим, что cos t = 0 и t =	π	,	3π	.
	2		2

При этих значениях t из выражения y = a sin 3 t находим, что y = ±a .

Полагая у = 0, находим, что sin t = 0 и t = 0,π . При этих значениях t из выражения y = a cos3 t находим, что х = ±а. Та-

151

ким образом, график функции пересекает координатные оси в

точках (a,0); (0,а); (-а,0); (0, -a).

Найдем

производные

y′y

xt′ = −3a cos2 t sin t,

yt′ = 3a sin 2 t cos t,

yt′ =

= −tgt,

y′′xx =

( y′

)′

Из выражения для

xt′

3a cos4

t sin t

y′

x′t

производной

определяем

критические

точки.

При

t = 0,

t = π производная равна нулю, а при t =

t =

3π

- не

существует.

Таким образом, область изменения параметра t разбива-

3π

ется на четыре интервала 0,

;

,π ;

π,

,2π .

2 2

> 0 , т. е. функ-

При t

, производная y′x < 0 , а y′x′

ция убывает и график функции направлен выпуклостью вниз.

При	π	,π		′		и	′′
	t		yx > 0				yxx > 0 , т. е. функция возрастает и
	2
график направлен выпуклостью вниз.
		3π		′			′′
При	t π,		y		< 0	и
		2					yxx < 0 , т. е. функция убывает и гра-

	3π
фик направлен выпуклостью вверх. При	t		,2π y′x > 0 , а
		2

y′xx′ < 0 , т. е. функция возрастает и график направлен выпукло-

стью вверх. Кстати, пользуясь симметрией графика функции, этот анализ можно было ограничить изменением параметра

	π
только одним интервалом, например, t 0,	2	.
	2

При t ={0,π} производная y′x = 0, y = 0 и касательные совпадают с осью x, т. е. точки (a,0) и (-a,0) будут точками

152

возврата. При t = π2 ; 32π производная y′x не существует, а при

x = 0, касательные совпадают с осью у и точки(0,a), (0,-a) будут также точками возврата. Учитывая все это, представим график функции (рис. 2.63). Полученная кривая представляет траекторию движения точки подвижного круга, катящегося изнутри по неподвижному кругу радиуса а, и называется астроидой.

Рис. 7.63

б) Функция определена при любом значении параметра t из интервала t [0,2π]. Найдем точки пересечения графика с

осями координат. При x = 0, sin t = t, t = 0 . При y = 0, cost =1, t = 0, t = 2π . Отсюда следует, что кривая при t=0 проходит через начало координат, а при t = 2π пересекает

ось Ох в точке x = 2πa .
Найдем производные						sin t
xt′ = a(1 − cos t),		yt′ = a sin t, y′x		=		sin t	,
xt′ = a(1 − cos t),		yt′ = a sin t, y′x		=	1	−cos t	,
					1	−cos t
y′′xx =	cos t(1 − cos t) −sin 2 t		= −			1		.
y′′xx =	a(1 − cos t)3		= −	a(1 − cos t)2				.
	a(1 − cos t)3			a(1 − cos t)2
Приравнивая y′x		к нулю, из уравнения sint = 0 находим

значения параметра в критических точках t ={0;π;2π} . Первая производная не существует при 1 − cos t = 0 , т. е. при значени-

153

ях параметра t ={0;2π} . При переходе параметра через крити-

ческие	значения	t ={0;2π} ,		т.е.	в	окрестности
(0 −ε,	0 +ε), (2π −ε,	2π +ε) , где	ε	> 0 , производная y′x ме-
(0 −ε,	0 +ε), (2π −ε,	2π +ε) , где	ε	> 0 , производная y′x ме-

няет знак с минуса на плюс. Отсюда следует, что касательная к графику функции в точках x ={0;2πa} параллельна оси Оу,

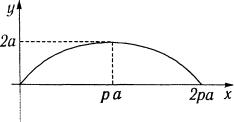
При t = π вторая производная y′xx′ < 0 , т.e. точка x = π a точка максимума функции у = 2а. Более того, поскольку y′xx′ < 0 нa всем интервале t [0,2π], то кривая на этом интервале выпукла вверх.

При изменении t от 0 до π производная y′x > 0 , следовательно, кривая возрастает. При изменении t от π до2π производная y′x < 0 , следовательно, кривая убывает. Все сказанное

позволяет представить график в виде (рис. 2.64). Полученная кривая представляет траекторию точки круга радиуса а катящегося без скольжения по прямой Ох за время одного оборота круга и называется циклоидой.

Рис. 2.64

в) Функция определена при всех значениях t, кроме t = -1. При t = 0 координаты х = 0, y = 0 и при t → ±∞ координаты x, y → 0 , т. е. начало координат служит особой точкой и

в нем кривая сама себя пересекает.

154

Найдем наклонную асимптоту. Угловой коэффициент ра-

y(t)

3at

1 + t

вен k = lim

= lim

= −1.

x(t)

1 +t

3at

x→−1

Параметр

3at

b = lim ( y(t) − kx(t)) = lim

1 + t

x→−1

= lim		3at	= −a
	1	−t + t 2
x→−1

Отсюда уравнение асимптоты x + y + a = 0.

При изменении t от − ∞до -1 , точка (х,у) из начала координат удаляется в бесконечность, причем значения х - положительны, а у - отрицательны, т. е. ограничены асимптотой, расположенной в четвертом квадранте.

При изменении t от -1 до 0 точка (х,у) из бесконечности возвращается к началу координат, причем значения x - отрицательны, а у - положительны, т. е. ограничены асимптотой, расположенной во втором квадранте. При изменении t от 0 до− ∞ точка описывает против часовой стрелки петлю, расположенную, судя по значениям х,у, в первом квадранте.

Обозначая t = xy , нетрудно перейти к уравнению функ-

ции в неявном видe F(x, y) = x3 + y3 −3axy = 0 . Находим производные

f x′ = 3(x2 − ay), Fy′ = 3( y 2 − ax), y′x = −	Fx′	= −	x2 − ay	.
	Fy′
			y 2 − ax

Приравнивая y′x = 0 и решая это уравнение совместно с уравнением F(x,y) = 0, находим критические точки х = 0, у = 0 и x = a3 2, y = a3 4 . Вычислим y′xx′ при x = a3 2 по формуле

155

y′′xx = −

Fxx′′

= −

Так

как

исследуемой точке

3( y 2 − ax)

Fy′

′′

yxx < 0 , то это точка максимума ymax = a

4, x = a

2 .

В точке (0,0) Fx′ = 0

Fy′ = 0 ,

поэтому можно утвер-

ждать, что касательными в этой точке служат оси координат. Учитывая все это, представим график функции (рис. 2.65). Полученная кривая называется декартовым листом.

Рис. 7.65.

2.15. Формула Тейлора и Маклорена

10. Если функция f (x) определена и дифференцируема n +1 раз в некоторой окрестности точки x0 = a , то она может

быть представлена в виде суммы многочлена n-ой степени и остаточного члена Rn (формула Тейлора)

f (x) = f (a) +		f ′(a)	(x −a) +
f (x) = f (a) +		1!	(x −a) +		(1)
		1!
	f ′′(a)			f (n) (a)
+	f ′′(a)	(x −a)2 +... +		f (n) (a)	(x −a)n + R
+		(x −a)2 +... +			(x −a)n + R
2!				n!	n
2!				n!

156

где	R =	f (n+1)	(c)(x −a)n+1	; c = a +θ(x −a) ; 0 <θ <1 –
где	R =			; c = a +θ(x −a) ; 0 <θ <1 –
	n		(n +1)!
			(n +1)!

остаточный член в форме Лагранжа.

Формула Тейлора (n-го порядка) позволяет представить функ-


цию	f (x) в виде многочлена n-ой степени и оценить с помо-
щью остаточного члена Rn						возникающую при этом погреш-
ность, которая может быть сделана сколь угодно малой.
	20. При а = 0 формула (1) принимает вид:
	f (x) = f (0) +			f ′(0)	x +	f ′′(0)	x2 +... +	f (n) (0)	xn + R ,	(2)
	f (x) = f (0) +				x +		x2 +... +		xn + R ,	(2)
		1!				2!		n!	n
		1!				2!		n!
где	R =	f (n+1) (θ x)	xn+1 ; 0 <θ <1, и называется формулой Мак-
где	R =		xn+1 ; 0 <θ <1, и называется формулой Мак-
	n	(n +1)!
		(n +1)!

лорена. К этому частному случаю формулу Тейлора можно

свести с помощью перехода к новой независимой переменной

ξ = x −a .

Остаточный член в формуле Тейлора иногда записывают в форме Пеано Rn = O((x −a)n ) , которая в ряде случаев бывает более удобна (вычисление пределов). Остаточный член в форме Пеано для формулы Маклорена имеет вид Rn = O(x)n .

15.1. Для функций а) ex ;

б) sin x;

в) cos x; г) (1 + х)n;

д) 1n(1 + х), написать формулу Маклорена n-го порядка и

оценить погрешность.

f (x) = ex , то f (n) (x) = ex при любом

Решение. а) Если

n=1,2,3, ...

f (n) (0) =1, то по формуле (2)

Так как f (0) =1 и

=1+

+…+

+ Rn .

Точность разложения определяется остаточным членом

R =

eθx

xn+1 . Оценим погрешность.

(n +1)!

157

Так как

n+1

то, например, при х = 1,

(n +1)!

10 2n+1

R (1)

; при x = 2,

R (2)

и т. д. При любом

(n +1)!

значении х при n → ∞ остаточный член стремится к нулю и чем больше n, тем точнее разложение. При x = 1 можно получить формулу для приближенного вычисления числа е

e =1+11! + 21! + 31! +... + n1! . б) Пусть f (x) = sin x , тогда f (0) = 0 ;

′

(x) = cos x = sin

x +

(0) =1;

′′

(x) = −sin x = sin

x +

(0) = 0 ;

′′′

−1 ;

(x) = cos x = sin x

(0) =

……………………..

(n)

(0) = sin n

= sin x + n

Разложение примет вид

sin x = x −

−... + (−1)m−1

x2m−1

+ R .

(2m −1)!

Остаточный член

x2m−1

sin(θ x +(2m +1) π ) ≤

2m+1

(2m +1)!

т. к.

sin α

≤1 и при

n → ∞ стремится к нулю независимо от

значения х.

f (x) = cos x , то

f (0) =1;

в) Если

′

(x) = −sin x = cos x +

(0) = 0 ;

158

159

′′

= −1;

(x)

= −cos x = cos x +2

(0)

′′′

= 0 ;

(x) = sin x = cos

x +

(0)

……………………..

(n)

(0) = cos n

= cos x + n

Разложение примет вид

cos x =1 −

−... + (−1)

m x2m

+ R .

(2m)!

Остаточный член

x2m+2

cos(θ x +(2m + 2) π ) ≤

2m+2

(2m + 2)!

(2m +2)!

т. к.

cosα

≤1 и при n → ∞

стремится к нулю независимо от

значения х.

г) Рассмотрим степенную функцию (1 + x)m , где m – любое вещественное число.

Разложим (1 + x)m по степеням х, т. е. в окрестности точки x0 = 0 .

f (x) = (1 + x)m ,					f (1) =1;
′		m−1		,	′
f (x) = m(1+ x)					f	(1) = m ;
′′	m−2		,		f	′′	;
f (x) = m(m −1)(1+ x)						(1) = m(m −1)
……………………..
f (k ) (x) = m(m −1)...(m −k +1)(1+ x)m−k ,
f (k ) (1) = m(m −1)...(m −k +1) .
Разложение примет вид

(1+ x)m =1+	m	x +	m(m −1)	x2 +... +	m(m −1)...(m −n +1)	xn + R ,

1!		2!			n!	n

где Rn = m(m −1)+...(m −n) xn+1 (1+θ x)m−n−1 , 0 <θ <1. (n 1)!

Здесь Rn → 0 с возрастанием n только при x ] −1,1[

т. е. погрешность может быть сколь угодно малой величиной только для значений из указанного интервала.

д) Находим производные и их значения в точке х = 0

′

=1;

1+ x

f (x)

(0)

′′

= − (1+ x)2 , f

−1

;

(x)

(0)

′′′

1 2

′′′

=1 2

= (1+ x)3

;

(x)

(0)

( 4) (x) = −

1 2 3

f ( 4) (0) = −1 2 3 ;

(1+ x)4

……………………..

Подставляя в формулу Маклорена, получим

ln(1+1) = x −

−

+... +(−1)

n−1

+ R ,

где Rn

(−1)n

n+1

n +1

1+θx

Погрешность вычисления логарифма Rn

→ 0 с возраста-

нием n только при x ] −1,1[ , т. е.

в полуоткрытом интервале.

15.2. Разложить многочлен x4 −2x3 + x2 +3x −5 по сте-

пеням двучлена x + 2 .

Решение.

Введем

обозначение

f (x) = x4 −2x3 + x2 +3x −5

и найдем производные:

′

−6x

′′

−12x +2 ,

f (x)

+ 2x +3 , f (x) =12x

′′′

(4)

(x) = 24 ,

(n)

(x)

= 0 для n ≥ 5 .

(x) = 24x −12 , f

При x = −2 имеем:

160

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 14 1516 / 2316 17 18 19 20 21 22 23 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.77 Mб02525.pdf
#
15.11.20221.78 Mб02528.pdf
#
15.11.20221.78 Mб12529.pdf
#
15.11.20221.79 Mб12530.pdf
#
15.11.20221.79 Mб12532.pdf
#
15.11.20221.8 Mб42536.pdf
#
15.11.20221.8 Mб02538.pdf
#
15.11.20221.81 Mб32539.pdf
#
15.11.20221.81 Mб12544.pdf
#
15.11.20221.81 Mб02545.pdf
#
15.11.20221.81 Mб02546.pdf