
2406
.pdf
a |
n |
cosnx |
b sin nx |
c |
n |
einx |
c |
n |
e inx |
|
|
n |
|
|
|
|
и, таким образом, частная сумма ряда Фурье запишется так:
a0 |
N |
|
|
N |
|
|
|
N |
(a cosnx |
b sin nx) |
c |
(c einx |
c |
|
e inx ) |
c einx. |
|
|
n |
|||||||
2 |
n |
n |
0 |
n |
|
|
n |
|
n 1 |
|
|
n 1 |
|
|
|
N |
Переходя в этом равенстве к пределу при N 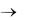 и обозначив
и обозначив
|
|
|
N |
|
|
|
|
|
|
|
|
|
lim |
c |
n |
einx |
|
c einx , |
|
|
|
|
|
N |
|
|
|
n |
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
получим: |
|
|
|
|
|
|
|
|
|
|
|
a0 |
N |
|
|
|
|
|
|
N |
|
f (x) lim |
(a cosnx |
|
b sin nx) |
lim c einx |
c einx , |
|||||
|
|
|||||||||
N |
2 |
n |
|
|
n |
|
|
N |
n |
n |
n 1 |
|
|
|
|
|
N |
|
|||
|
|
|
|
|
|
|
|
|||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
c |
n |
einx . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найдем теперь выражения для коэффициентов cn . Действительно, если учесть выражения для an и bn , то получим:
cn |
an ibn |
|
1 |
|
1 |
f (x) cosnxdx i |
1 |
f (x) sin nxdx |
2 |
2 |
|
|
|
||||
|
|
|
|
|
|
|||
83

|
|
|
1 |
f (x)(cosnx i sin nx)dx |
1 |
|
|
f (x)e inx dx, |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
2 |
2 |
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
то есть |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
c |
|
|
|
1 |
|
|
f (x)e |
inx dx, |
(n |
|
|
1,2,...), |
||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
2 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
c0 |
|
a0 |
|
1 |
|
f (x)dx, |
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
c |
|
|
an ibn |
1 |
|
|
|
1 |
|
f (x) cosnxdx |
|
i |
1 |
f (x) sin nxdx |
||||||||||
n |
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
f (x)(cosnx |
|
|
i sin nx)dx |
1 |
|
|
f (x)einx dx, (n 1,2,...). |
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
2 |
|
|
|
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Нетрудно видеть, что при всех целых n справедливо равенство
c |
|
1 |
f (x)e |
inx dx, (n 0, 1, 2,...), |
|
n |
|
||||
2 |
|||||
|
|
|
|||
|
|
|
|
при этом интегрирование можно вести по любому отрезку длины 2 .
Выражение сn einx называется комплексной формой ряда
Фурье функции f(x).
84

|
Пример 3. Записать ряд Фурье в комплексной форме |
||||
для периодической функции f(x) периода T 2 |
, опреде- |
||||
ленной при 0 x |
2 |
равенством f (x) e x . |
|
||
|
От комплексной формы перейти к действительной |
||||
форме ряда Фурье функции f(x). |
|
||||
|
Решение. |
1) |
По формулам (3.1), (3.2) |
запишем |
|
f (x) |
с |
einx , при этом |
|
||
|
n |
|
|
|
|
|
|
1 |
2 |
f (x)e inx dx |
1 |
2 |
e x |
e inx dx |
1 |
2 |
in) x dx |
|||||||||||||||||||||
cn |
|
|
|
|
|
|
|
|
|
|
|
|
|
e(1 |
||||||||||||||||||
2 |
|
|
2 |
|
|
|
2 |
|||||||||||||||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1 |
|
|
|
|
1 |
e(1 |
in) |
|
2 |
1 |
|
|
|
|
|
1 |
|
(e2 |
|
1), |
|
(n |
0, |
1, 2,...) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 |
1 |
|
in |
|
|
|
|
|
2 |
1 |
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
0 |
in |
|
|
|
|
|
|
|
||||||||||||||||||
или, иначе, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
cn |
|
|
e2 |
1 1 |
|
in |
|
(n |
0, |
1, |
2,...). |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
1 |
|
n2 |
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
Подставляя cn (n |
|
0, 1, 2,...) в ряд для f(x), полу- |
||||||||||||||||||||||||||||
чим ряд Фурье этой функции |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
f (x) |
|
e2 |
1 |
|
|
|
|
|
1 |
|
in |
einx , |
0 |
|
x |
2 . |
|
||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
n2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
2) Если учесть, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
a |
|
|
|
2 Re(cn ), n |
0,1,2K , |
|
bn |
|
2 Im(cn ), |
n |
1,2K , |
|||||||||||||||||||||
то найдем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
85

an |
e2 |
1 |
|
|
1 |
|
, |
n |
0,1,2K, |
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
n2 |
||||||||
|
|
|
|
|
|
|
||||||
bn |
e2 |
1 |
|
1 |
|
|
, |
n |
1,2K |
|||
|
|
|
|
|
|
|
|
|||||
|
|
1 |
n2 |
|
||||||||
|
|
|
|
|
|
|
||||||
и, значит,
f (x) |
e2 |
1 1 |
|
cosnx |
|
n sin nx |
при 0 x 2 . |
||
|
|
|
|
|
|
|
|
||
|
|
|
2 |
n 1 1 n2 |
|
1 n2 |
|||
|
|
|
|
||||||
Или в другом виде
e x |
e2 |
1 1 |
|
cosnx |
|
n sin nx |
при 0 x 2 . |
||
|
|
|
|
|
|
|
|
||
|
|
|
2 |
n 1 1 n2 |
|
1 n2 |
|||
|
|
|
|
||||||
3.6. Комплексная форма ряда Фурье для периодической функции периода T=2l.
Пусть f(x) – периодическая функция периода T=2l, удовлетворяет условиям разложимости в ряд Фурье. Тогда под-
становка x |
l |
t приводит к функции f |
lt |
с периодом |
|
|
2 , разложимой в ряд Фурье. Для такой функции по формулам (1), (2) имеем:
f |
lt |
cn eint , где cn |
1 |
f |
lt |
e inx dt. |
|
2 |
|
||||
|
|
|
|
|
|
86
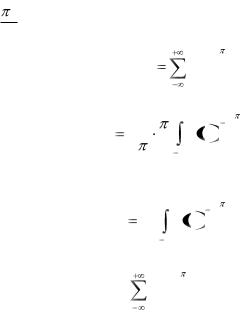
Переходя к аргументу x, с помощью подстановки t  lx получим:
lx получим:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
n |
|
x |
|
|
|
||
|
|
|
|
f (x) |
|
|
|
|
|
c |
e |
|
l |
, |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
при этом |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
l |
|
|
|
|
|
i |
n |
x |
|
||||
c |
n |
|
|
|
|
|
|
|
|
f x e |
|
dx |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
||||||||
|
|
2 |
|
|
|
|
l |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|||
или окончательно |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
l |
|
|
|
|
i |
n |
|
x |
|
|
|
|||||
|
|
c |
n |
|
|
|
f |
x e |
l |
|
dx. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2l |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
i |
n |
x |
|
|
|
|
|
|
|
|
|
|
Выражение |
|
|
|
|
|
|
c |
n |
e |
l |
называется комплексной |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
формой ряда Фурье этой функции f(x).
87
Расчетные задания
Задача 1. Периодический сигнал f(t) разложить в тригонометрический ряд Фурье. Вычертить графики сиг-
нала f(t) и частичных сумм S1 (t), |
S2 (t) ряда Фурье. |
||||||||||||||||
1. |
f (t) |
t |
1 на [ |
1;1], f (t |
|
2) f (t) . |
|
||||||||||
2. |
f (t) |
2 |
|
| t | на [ |
1;1], |
f (t |
|
2) |
f (t) . |
||||||||
3. |
f (t) |
| 1 |
|
t | на [ |
2;2], |
f (t |
|
4) |
f (t) . |
||||||||
4. |
f (t) |
1 |
| t | на [ |
1;1], |
f (t |
2) |
f (t) . |
||||||||||
|
|
|
|
|
|
|
t |
|
, если |
|
|
t |
0 |
|
|
||
|
|
|
2 |
|
|
|
|
|
|
|
|||||||
5. |
f (t) |
|
|
|
|
|
|
|
|
|
|
, f (t |
2 ) f (t) . |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
, |
|
если 0 |
|
t |
|
|
|
|
||||
|
|
|
4 |
|
|
|
|
|
|
||||||||
6. |
f (t) |
t 2 |
|
t на [ |
1;1], |
f (t |
2) |
f (t) . |
|||||||||
|
|
t, если |
|
2 |
t |
|
0 |
|
|
|
|
||||||
7. |
f (t) |
0, если |
0 |
t |
2 |
, |
f (t |
4) |
f (t) . |
||||||||
|
|
2, если |
2 |
t |
|
4 |
|
|
|
|
|||||||
8. |
f (t) |
(t |
1)2 |
|
на [ |
2;2], |
f (t |
4) |
f (t) . |
||||||||
9. |
f (t) |
2 |
|
t, |
|
если |
1 |
t |
|
0, |
f (t |
2) f (t) . |
|||||
|
|
|
1, |
если |
0 |
t |
|
1 |
|
|
|
||||||
88
10. |
f (t) |
et |
на [ |
; |
], |
f (t |
2 |
) |
f (t) . |
|
||
11. |
|
1, |
если |
1 |
t |
0 |
|
|
f (t) . |
|||
f (t) |
1, |
если |
0 |
|
t |
1 |
, |
f (t |
2) |
|||
|
|
|
t, если |
0 |
|
t |
1 |
|
|
|
||
12. |
f (t) |
2, если |
1 |
t |
2 |
, |
f (t |
3) |
f (t) . |
|||
|
|
3 |
|
t, если |
2 |
t |
|
3 |
|
|
|
|
13. |
f (t) |
t 2 , |
если |
|
1 |
e |
|
0 |
f (t |
2) |
f (t) |
|
|
|
|
|
|
|
|
, |
|||||
|
|
|
1, |
если |
0 |
t |
1 |
|
|
. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
f (t) |
e t |
на [ 1;1], |
f (t |
|
2) |
f (t) . |
|
||||
15.f (t)
16.f (t)
17.f (t)
|
|
|
|
1, если |
|
t |
0 |
|
|
|
|||||
|
2 |
(t |
)2 |
, если 0 |
1, |
f (t |
2 |
) f (t) . |
|||||||
2 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1 |
, |
если |
1 |
|
t |
0 |
|
|
|
|
|
||
|
|
f (t 2) |
|
f (t) . |
|||||||||||
2 |
|
|
|
|
|
|
, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
t, |
если |
0 |
|
t |
1 |
|
|
|
|
|
|||
|
|
t |
|
, если |
|
|
|
t |
0 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
t, если |
0 |
t |
|
|
|
, f (t |
2 |
) |
f (t) . |
|||||
2 |
|
||||||||||||||
0, |
если |
|
|
t |
0 |
|
|
|
|
|
|||||
2 |
|
|
|
|
|
|
|||||||||
89

18. |
|
t, |
если |
1 |
|
t |
0 |
|
|
|
|
f (t) . |
||||||
f (t) |
|
t 2 , если |
0 |
|
t |
1, |
f (t |
|
2) |
|||||||||
19. |
f (t) |
t |
2, |
если |
|
2 |
t |
|
0, f (t |
4) |
f (t) . |
|||||||
|
|
|
|
|
|
2, |
если |
0 |
t |
2 |
|
|
|
|
|
|||
20. |
f (t) |
t |
t 2 |
на [ |
1;1], f (t |
2) |
f (t) . |
|
|
|||||||||
21. |
f (t) |
1 |
|
t 2 , |
если |
|
1 |
t |
|
0 |
f (t |
4) |
f (t) |
|||||
|
|
|
|
1, |
|
если |
0 |
t |
1 |
|
, |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1, если |
2 |
|
t |
1 |
|
|
|
|
|
|
|||||
22. |
f (t) |
t 2 , если |
1 |
t |
1 |
, |
f (t |
4) |
|
f (t) . |
||||||||
|
|
|
|
|
|
1, если |
1 |
|
t |
2 |
|
|
|
|
|
|
||
23. |
f (t) |
t 2 |
2t |
2 на [ |
2;2], |
f (t |
4) |
f (t) . |
||||||||||
|
|
t, |
если |
1 |
|
t |
0 |
|
|
|
|
|
|
|||||
24. |
f (t) |
|
1 |
, если |
0 |
|
t |
1, |
f (t |
|
2) |
f (t) . |
||||||
|
|
2 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
1 |
|
, если |
2 |
t |
1 |
|
|
|
|
|
|||||
|
|
4 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
25. |
f (t) |
|
1, если |
1 |
|
t |
2 |
, |
f (t |
4) |
|
f (t) . |
||||||
|
|
2 |
t, если |
1 |
t |
2 |
|
|
|
|
|
|
||||||
90
Задача 2. Продолжая функцию f(x) четным или нечетным образом, разложить ее в ряд Фурье в № 1.-12 по косинусам, в № 13-25 по синусам.
1. |
f (t) |
t 2 |
t на [ |
1;0] . |
|
|
|
|
|||
|
|
|
1, если 0 |
t |
|
|
|
|
|||
2. |
f (t) |
|
|
2 |
|
. |
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
|
t, если |
|
t |
|
|
|
|||
|
|
|
2 |
|
|
|
|||||
3. |
f (t) |
(t |
2)2 , |
если 0 |
|
t |
2 . |
||||
4. |
f (t) |
|
2, если 0 |
t |
1 . |
|
|||||
|
|
2 |
t, если 1 |
t |
|
2 |
|
||||
5. |
f (t) |
t 2 , если 0 |
|
t |
1 |
. |
|
|
|||
2, если 1 |
|
t |
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|||||
|
|
1, если |
|
2 |
t |
|
1 |
||||
6. |
f (t) |
1 |
t 2 , если |
1 |
|
t |
0 . |
||||
7. |
f (t) |
t 2 , |
если 0 |
|
t |
2 . |
|
|
|||
8. |
f (t) |
|
1, если 0 |
t |
|
1 |
2 . |
||||
|
t 2 2t, если 1 |
|
t |
||||||||
|
f (t) |
1, если 0 |
|
t |
1 |
|
|
|
|
||
9. |
t 2 , если 1 |
|
t |
2 . |
|
|
|||||
91
10. |
f (t) |
t 3 |
t, |
если 1 |
t |
2 . |
|
|
|
1 |
t, если 0 |
t |
1 |
11. |
f (t) |
|
t 2 |
t, если 1 |
t |
2 . |
12. |
f (t) |
t 2 |
t |
2, если 0 |
t 1. |
|
13. |
f (t) |
2, если 0 |
|
t |
1. |
|
|
|
|
||
|
|
t, если 1 |
t |
2 |
|
|
|
|
|
||
14. |
f (t) |
|
2, если 0 |
t |
|
1 |
2 . |
||||
1 |
t 2 , если 1 |
t |
|
|
|
||||||
|
|
|
2, если 0 |
t |
|
|
|
|
|
||
15. |
f (t) |
|
|
2 |
. |
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
|
|
t, если |
|
|
t |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|||
16. |
f (t) |
t 2 |
t, если |
|
|
1 |
|
|
t |
0 . |
|
17. |
f (t) |
|
2, если 0 |
|
|
t |
1 . |
||||
|
|
2 |
t, если 1 |
t |
|
2 |
|||||
18. |
f (t) |
(t |
1)2 , если 0 |
t |
1. |
||||||
19. |
f (t) |
t 2 , если 0 |
|
t |
1 |
. |
|
|
|||
1, если 1 |
t |
2 |
|
|
|||||||
|
|
|
|
|
|
||||||
92
