2406

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Функции f (x)

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.55 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

		2				2		1	x	x	2		x 3			,

		3		x		3			3	3			3
		3		x		3			3	3			3
или
	2		2		2		x 2		x2	2		x3		2	xn	,

	3 x 3			3		3 3			32	3	33			3	3n

где 1	x	1	, т.е.	3 x 3 .

	3

2.2.Приближенное вычисление значений функции

Пусть требуется вычислить значение функции f (x) при x x1 с заданной точностью 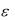0 .

Если функцию

f (x) в интервале

( R, R) можно

разложить в степенной ряд

f (x)

a x a

и x1 ( R, R) , то точное значение

f (x1 )

равно сумме этого

ряда при x x1 , т.е.

f (x )

a x a

2 1

n 1

а приближенное – частичной сумме Sn (x1 ) , т.е.

f (x )

(x )

a x a

xn .

1 1

n 1

Точность этого равенства увеличивается с ростом n . Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.

f (x1 ) Sn (x1 )rn (x1 ) ,

где

r (x )	a	xn 1	a	xn 2	.
n 1		n 1 1		n 2 1

Таким образом, ошибку f (x1 ) Sn (x1 ) можно найти, оценив остаток rn (x1 ) ряда.

Для рядов лейбницевского типа

rn (x1 )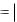un 1 (x1 ) un 2 (x1 ) un 3 (x1 ) un 1 (x1 ) .

В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти (подобрать) положительный ряд с большими членами (обычно это сходящийся ряд геометрической прогрессии), который легко бы суммиро-

вался. И в качестве оценки					rn (x1 )	берут величину остатка
этого нового ряда.
Пример 1. Найти sin1 с точностью до 0,001.
Решение. Согласно формуле (2.2),
	1	3	1 5				n 1	1	.
sin1 1		1		1		( 1)
sin1 1		1		1		( 1)
	3!		5!		n 1			(2n 1)!

Стоящий справа ряд сходится абсолютно (проверить само-

стоятельно).

Так

как

0,008(3) 0,001,

0,0002

0,001, то для нахождения sin1 с точностью до

0,001 достаточно первых трех слагаемых:

sin1

0,842 .

Допускаемая при этом ошибка меньше, чем первый отброшенный член (т.е. меньше, чем 0,0002). Вычисленное микрокалькулятором значение sin1 примерно равно 0,84174.

Пример 2. Вычислить число e					с точностью до 0,001.
Решение. Подставив x			1 в формулу (2.1), получим:
	1	1	1
e 1					.
	1!	2!		n!

Справа стоит знакоположительный ряд. Возьмем n слагаемых и оценим ошибку rn (x) :

rn	(x)		1					1				1

		(n 1)! (n						2)!			(n	3)!
		(n 1)! (n						2)!			(n	3)!
			1					1		1				1

					(n		1)!			n	2		(n 2)(n			3)
	1		1				1			1				1			1				1		,

	(n 1)!					n	1		(n	1)	2				(n	1)!				1		n! n
																	1			1

																		n		1
																		n		1
где r (x)			1				. Остается подобрать наименьшее натураль-
где r (x)							. Остается подобрать наименьшее натураль-
	n			n! n
				n! n
ное число n , чтобы выполнялось неравенство																				1	0,001.

																			n! n
																			n! n

Нетрудно вычислить, что это неравенство выполня-

ется при n		6 . Поэтому:
e	1	1	1	1	1	1	1	2	517	2,718 .
e	1	1	2!	3!	4!	5!	6!	2	720	2,718 .
			2!	3!	4!	5!	6!		720

Замечание. Оценку остатка ряда можно производить с помощью остаточного члена ряда Маклорена

f (x1 ) Sn (x1 )	Rn	(x1 )	f (n 1) (c)		,
			f (n 1) (c)
			(n	1)!
			(n	1)!

где c находится между 0 и x1 . В последнем примере

R (1)

, 0 c

1. Так как ec

3, то

1)!

(1)

. При n

6 получим:

1)!

R6 (1)

0,001

e 1 1

2,718.

2.3. Приближенное вычисление определенных интегралов

Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных ин-

тегралов в случаях, когда первообразная не выражается в конечном виде через элементарные функции, либо нахождение первообразной сложно.

Пусть требуется вычислить 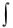f (x)dx с точностью до

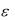0 . Если подынтегральную функцию f (x) можно разложить в ряд по степеням x и интервал сходимости

( R, R) включит в себя отрезок [a,b] , то для вычисления

заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функции.

												1 4
Пример. Вычислить интеграл												e x2 dx с точностью
												0
0,001.
Решение. Разложим подынтегральную функцию в
ряд Маклорена, заменяя x								на ( x 2 )				в формуле (2.1):
	2		x	2		x	4		x	6
e x		1	x			x			x		, x		(	,	)	(2.11).


			1!		2!			3!
			1!		2!			3!
Интегрируя обе части равенства (2.11) на отрезке															0,	1	,
Интегрируя обе части равенства (2.11) на отрезке															0,	4	,
																4
лежащем внутри интервала сходимости (													,	) , получим:

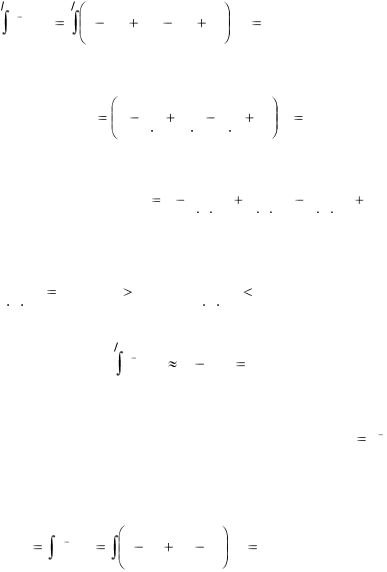
1 4			2		1 4		x	2		x		4		x		6
	e	x	2	dx		1	x			x				x				dx
		x
							1!				2!			3!
0					0		1!				2!			3!
0					0
																						1
											x		3		x		5			x	7			4
								x			x				x					x

										1! 3				2! 5					3! 7					0
													1				1					1		0	1	.
													1				1					1			1

													4 1! 3 43									2! 5 45 3! 7 44
Получили ряд лейбницевского типа. Так как
1					0,0052				0,001, а								1						0,001, то с точностью

1! 3		43															1! 3		45
1! 3		43															1! 3		45
до 0,001 имеем:
							1 4							1					1
								e x		2	dx			1					1			0,245 .

														4			192
							0							4			192
							0
Замечание. Первообразную F(x) для функции																									f (x)	e x2

легко найти в виде степенного ряда, проинтегрировав равенство (2.11) в пределах от 0 до x :

	x	2		x		t	2		t	4
F(x)	e t	2	dt		1	t			t		dt

						1!		2!
	0			0		1!		2!
	0			0

	x3 x5		x7
x				, x ( , ) .
	1! 3	2! 5	3! 7

и F(x) 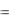f (t) dt играют очень

важную роль в теории вероятностей. Первая – плотность стандартного распределения вероятностей, вторая –

			1			x	t 2
функция Лапласа F (x)			1			e	2	dt (или интеграл веро-


			2
			2		0
ятностей). Итак, мы получили, что функция Лапласа
представляется рядом
	1		x3			x5			x7
F(x)		x								,
			2 3	22 2! 5					23 3! 7
	2		2 3	22 2! 5					23 3! 7

который сходится на всей числовой оси.

2.4. Приближенное решение дифференциальных уравнений

Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.

Рассмотрим два способа решения дифференциальных уравнений с помощью степенных рядов.

Пусть, например, требуется решить уравнение

f (x, y, y ) ,

(2.12)

удовлетворяющее начальным условиям

y		y0 , y	y0 .	(2.13)
	x	x0	x x0

Способ последовательного дифференцирования

Решение y y(x) уравнения (2.12) будем искать в виде ряда Тейлора:

y y(x		)	y (x0 )	(x x		)	y (x0 )	(x x		)2
	0		1!		0		2!		0

при этом первые два коэффициента найдем из начальных условий (2.13). Подставив в уравнение (2.12) значения

x x0 , y y0 , y y0 , найдем третий коэффициент

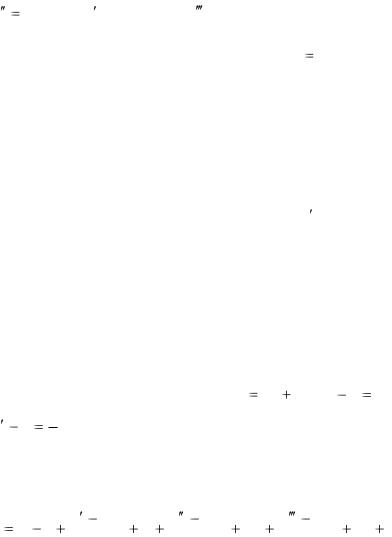
y	0	f (x	0	, y	0	, y	0	) . Значения	y	(x	0	), y(4) (x	0	), находим
	0		0		0		0				0		0

путем последовательного дифференцирования уравнения (2.12) по x и вычисления производных при x x0 . Най-

денные значения производных (коэффициентов) подставляем в равенство (2.14). Ряд (2.14) представляет искомое частное решение уравнения (2.12) для тех значений x , при которых он сходится. Частичная сумма этого ряда будет приближенным решением дифференциального уравнения

(2.12).

Рассмотренный способ применим и для построения общего решения уравнения (2.12), если y0 и y0 рассматривать как произвольные постоянные.

Способ последовательного дифференцирования применим для решения дифференциальных уравнений любого порядка.

Пример. Методом последовательного дифференцирования найти пять первых членов (отличных от нуля) раз-

ложения в ряд решения уравнения y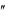 x 2 y 2 , y( 1) 2,

y ( 1) 12 .

Решение. Будем искать решение в виде

y y( 1)	y ( 1)	(x 1)	y ( 1)	(x 1)2	y ( 1)	(x 1)3
	1!		2!		3!

Здесь y( 1) 2, y ( 1)	1	. Найдем	y (	1) , подставив
	2

x 1 в исходное уравнение y ( 1)			(	1)2 22 5 . Для

нахождения последующих коэффициентов дифференцируем заданное дифференциальное уравнение:

y	2x 2yy ,
y (4)	2 2( y )2	2 yy ,
y (5)	4 y y 2 y y	2 yy	6 y y 2 yy ,

При x 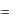1 получим:

y ( 1)		2	2	2			1	0	,
						2

y(4) (	1)	2	2		1	2		2 5	22,5 ,
				4

y(5) (	1)	6	1	5		2		2 0	15 ,
			2

<<< < Предыдущая 1 2 3 45 / 105 6 7 8 9 10 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.53 Mб02397.pdf
#
15.11.20221.53 Mб02398.pdf
#
15.11.20221.54 Mб22402.pdf
#
15.11.20221.54 Mб02403.pdf
#
15.11.20221.55 Mб02405.pdf
#
15.11.20221.55 Mб02406.pdf
#
15.11.20221.55 Mб02409.pdf
#
15.11.20221.56 Mб02413.pdf
#
15.11.20221.56 Mб02414.pdf
#
15.11.20221.57 Mб02418.pdf
#
15.11.20221.57 Mб12419.pdf