2250

При парной перестановке вершин A и B могут исчезнуть только пересечения ребер, инцидентных этим вершинам, а число пересечений ребер, инцидентных неподвижным вершинам, не изменяется.

Пусть в некотором графе ребра, инцидентные вершине A, имеют следующее число пересечений с остальными ребрами графа:

После перестановки местами вершин A и B число пересечений изменится и станет равным:

Тогда изменение числа пересечений в результате перестановки вершин A и B

выразится формулой :

Если SAB > 0, то перестановка вершин A и B целесообразна, так как ведет к уменьшению числа пересечений.

Определить наличие пересечений p[(i,j);(k,l)] между ребрами (i,j) и (k,l) можно следующим образом в соответствии с рис. 5.3, 5.4

Ребра А1А2 и В1В2 являются отрезками прямых линий. Прямая линия описывается уравнением /8/:

y = kx + b.

Прямая, на которой лежит отрезок А1А2 описывается уравнением :

Аналогично для В1В2:

63

Точка Z пересечения этих прямых имеет координаты :

Необходимо далее определить, принадлежит ли точка Z(x*,y*) обоим отрезкам А1А2, В1В2 в соответствии с рис. 5.3.

Это значит, что xmin < x* < xmax, ymin < y* < ymax, для каждого отрезка, где

хmin – большее значение из двух минимальных значений координаты х отрезков А1А2 и В1В2;

ymin – большее значение из двух минимальных значений координаты y отрезков А1А2 и В1В2;

хmax – меньшее значение из двух максимальных значений координат х отрезков А1А2 и В1В2;

ymax – меньшее значение из двух максимальных значений координат y отрезков А1А2 и В1В2.

66

где dmax - расстояние между самой дальней точкой одного отрезка и самой дальней точкой другого отрезка;

dA1A2 – длина отрезка А1А2; dB1B2 – длина отрезка B1B2.

Длины отрезков вычисляются по формуле: d = |xi - xj| + |yi - yj|

Все эти условия и ограничения были реализованы программно для оптимизации размещения элементов на коммутационном поле с минимизацией числа пересечений.

В качестве примера решения задачи минимизации числа пересечений при оптимизации размещения модулей на коммутационном поле с помощью ПЭВМ рассмотрим следующий.

Исходные данные:

количество модулей = 10

схема соединений представлена матрицей смежности (табл. 5.2)

координаты начального размещения модулей представлены в табл. 5.3

На рис. 5.9 показана схема соединений модулей, расположенных в исходных (до оптимизации) позициях с числом пересечений 129.

В результате решения этой задачи с помощью программы, реализующей алгоритм парных перестановок, получили новое (оптимальное) размещение модулей,

указанное в табл. 5.4, с числом пересечений, равным 10 (локальный минимум; глобальный

67

минимум, как будет показано в следующем разделе, равен 6). До оптимизации число пересечений было равно 129, то есть число пересечений уменьшилось после оптимизации почти в 13 раз. Схема соединений модулей, расположенных в позициях, после оптимизации показана на рис. 5.10. На рис. 5.9 и 5.10 цифра у линии показывает число соединений между модулями. Цифра 1 не проставляется.

5.2. Исследование зависимости эффективности алгоритма парных перестановок от

исходных начальных размещений и способы повышения его эффективности

Одним из методов оптимизации размещения элементов с минимизацией числа пересечений является алгоритм парных перестановок /1,2/. Согласно этому алгоритму,

сначала все элементы схемы произвольным образом размещаются по заданному количеству установочных позиций, а затем производятся перестановки тех пар элементов,

находящихся в разных позициях, которые дают уменьшение числа пересечений трасс. В

результате таких перестановок достигается локальный минимум. Близость его к глобальному минимуму, т.е. степень оптимизации, существенно зависит от исходного начального (обычно произвольного) размещения элементов в позициях. В связи с этим целесообразно исследовать зависимость степени оптимизации от начальных размещений.

Для этого необходимо разработать программу, реализующую алгоритм парных перестановок с использованием большого количества начальных размещений. Для каждого начального размещения должна быть проведена своя оптимизация. Для создания большого количества начальных размещений можно использовать функцию рандомизации, включив эту функцию в программу. Для облегчения обработки статистических данных в программе следует предусмотреть вывод результатов оптимизации в порядке уменьшения степени оптимизации с указанием количества появлений каждого оптимума. Отдельно вывести наилучший оптимум с указанием размещения элементов по позициям. Для оценки степени оптимизации необходимо сравнить оптимумы между собой.

Поставленные задачи были нами решены. Была разработана программа оптимального размещения элементов с получением большого количества исходных начальных размещений методом рандомизации.

3

68

Рис. 5.10. Схема соединений модулей, расположенных в позициях после оптимизации (количество пересечений 10).

70

Особенности результатов решения.

1) При оптимизации любого исходного начального размещения модулей число пересечений уменьшается по сравнению с неоптимизированным в несколько раз. В нашем примере число пересечений уменьшилось со 129 до 6 (глобальный минимум), то есть в

21,5 раза; схема соединений для наилучшего размещения представлена на рис. 5.11.

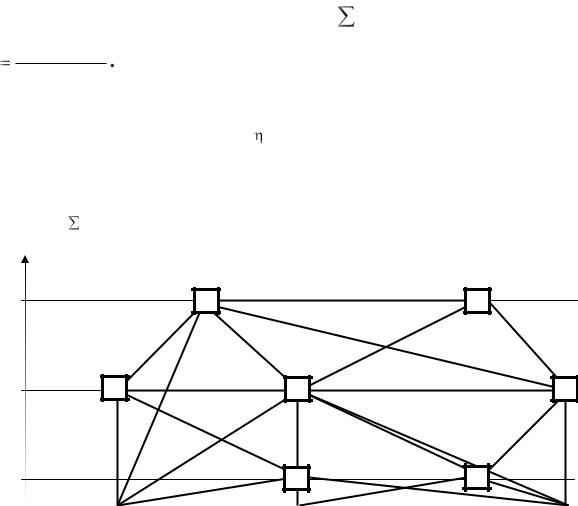
2) Степень оптимизации, т.е. значение минимума пересечений, в значительной степени зависит от начального размещения элементов в установочных позициях (рис.

5.12).

η Wi min - Wo min 100 %, показывающей насколько процентов полученный результат

Wo min

оптимизации отличается от глобального, монотонно возрастает, асимптотически приближаясь к единице при значениях , равных 290-300 % (рис. 5.13). По этому рисунку можно определить суммарную вероятность появления результата оптимизации,

отличающегося от глобального на заданное значение в процентах. Суммарная вероятность Pi - это сумма вероятностей i-го и всех предыдущих (лучших) минимумов.