
1800
.pdf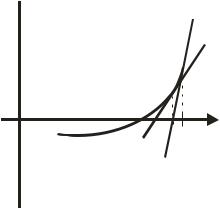
4) На шагес номером n |
|
|
xn xn 1 |
f xn 1 |
|
f xn 1 |
|
|
Если последовательность xn является сходящейся при n→∞, то данный алгоритм позволяет определить искомый корень.
 y
y
x
|
|
x2 x1b |
|
|
|
a |
||
Рис. 5.5. Иллюстрация метода касательных
В качестве примера приведём программу, которая находит корни уравнения x3 5x2 2x 5 методом дихотомии.
Program UrawNenie; {Точность задаём константой} const Eps=1e-6;
Var a,b,d :real;{Границы и середина отрезка} Res :real; {Результат}
{Функция, описывающая уравнение} Function f(x:real):real;
Begin f:=x*x*x-5*sqr(x)+2*x+5;
110
end;
{Начало программы} Begin
{Границы отрезка локализации коня вводим с клавиатуры}
Write('Введите границы отрезка:'); ReadLn(a,b);
if f(a)*f(b)>0
then WriteLn('Отрезок задан неверно!!!')
else {Находим корень} begin
{Выполнять пока длина отрезка больше точности}
repeat
d:=(a+b)/2; {Находим середину отрезка} if f(a)*f(d)<0 then b:=x
else a:=x; until (b-a<2*Eps);
{результат – середина отрезка} Res:=(b+a)/2;
WriteLn('Решение уравнения: ',Res); end;
End.
Если уравнение настолько сложное, то найти отрезок локализации не удаётся, то можно предусмотреть в программе поиск отрезка, например, так:
a:=-6; b:=a+0.1; While f(a)*f(b)>0 do
begin a:=b; b:=b+0.1; end;
111
Практические задания
Составить программу, которая одним из рассмотренных методов находит все корни уравнения
1.x3 x 2x2 2.
2.x3 12 x 3x 4 .
3.x3 4x x 1 .
4.x3 x2 8x 12.
5.x2 ln x.
6.ln x 2 x3.
7.x2 2sin x 1.
8.x2 2sin 2x 1.
9.x3 3x2 5x 12 .
10.x3 2sin 3x 1.
11.ln x2 1 1.
12.ln x4 1 2.
13.arctg 2x2 2 1.
14.2x3 4x x 1 .
15.x4 x 2.
16.x4 5x 3.
17.x4 5x 3 ln x .
18.x2 sin x 2 x .
19.x2 sin x 8 x.
20.x2 sin x lgx x.
21.x2 cosx 7 4x .
22.x2 cosx 7 4x .
23.x4 cosx 5.
24.3x3 2x2 5x 2 .
25.3x3 2x2 3x 1.
112
ЛАБОРАТОРНАЯ РАБОТА № 6
МЕТОДЫ ЧИСЛЕННОГО ИНТЕГРИРОВАНИЯ
Цель работы: ознакомление с методами численного решения нелинейных уравнений.
Теоретические сведения
В практической работе радиоинженера зачастую возникает необходимость вычисления интегралов, которые либо трудно, либо невозможно вычислить аналитически.
b
Определенный интеграл I f x dx можно трактовать
a
как площадь фигуры под графиком подынтегральной функции, то есть как площадь криволинейной трапеции. Многие методы численного интегрирования основаны на разбиении интервала интегрирование на более мелкие отрезки, на которых можно применить простые формулы для площади маленькой трапеции. Затем площади маленьких трапеций складываются.
Разобьем, например, отрезок интегрирования на N равных отрезков дискретизации длиной h b a 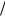 N точками a x0,x1,...,xN b. Если отрезки дискретизации довольно малы, то на каждом отрезке площадь трапеции можно приближенно заменить площадью прямоугольника. Прямоугольники можно строить, опираясь на левую или правую сторону отрезка. Отсюда получаем метод левых или правых прямоугольников. Ясно, что с увеличением числа отрезков, сумма площадей прямоугольников все с большей точностью будет совпадать с площадью криволинейной трапеции.
N точками a x0,x1,...,xN b. Если отрезки дискретизации довольно малы, то на каждом отрезке площадь трапеции можно приближенно заменить площадью прямоугольника. Прямоугольники можно строить, опираясь на левую или правую сторону отрезка. Отсюда получаем метод левых или правых прямоугольников. Ясно, что с увеличением числа отрезков, сумма площадей прямоугольников все с большей точностью будет совпадать с площадью криволинейной трапеции.
113
Формулы для приближенного вычисления интеграла называют квадратурными формулами. В общем виде квадратурная формула может быть записана как
b |
N |
N |
|
I f x dx Ak f xk Ak fk . |
(6.1) |
||
a |
k 1 |
k 1 |
|
Здесь fk f xk . Методы численного интегрирования отли-
чаются друг от друга способами задания коэффициентов Ak и точек отсчетов tk .
Перечислим некоторые формулы приближенного интегрирования, основанные на (6.1).
1. а) Формула левых прямоугольников
b |
N 1 |
|
||||
f x dx |
b a |
f0 f1 ... fN 1 h f a kh , |
(6.2) |
|||
|
|
|||||
|
|
N |
k 0 |
|
||
a |
|
|||||
б) формула правых прямоугольников |
|
|||||
b |
N |
|
||||
f x dx |
b a |
f1 f2 |
... fN h f a kh . |
(6.3) |
||
|
||||||
|
|
N |
k 1 |
|
||
a |
|
|||||
Здесь h b a 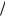 N – шаг интегрирования.
N – шаг интегрирования.
2. Формула трапеций
b |
f x dx |
b a |
f |
0 |
|
|
|
|
|
|
|
f |
N |
|
|
|
|
f |
... f |
|
|
|
|
||||||||||
|
|
|
N 1 |
|
|
|
||||||||||
|
|
|
|
|
|
|||||||||||
|
N |
|
2 |
1 |
|
|
|
|
|
2 |
|
|
||||
a |
|
|
|
|
|
|
|
|
(6.4) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
N |
|
|
|
|
|
f a f b |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
h f a kh |
|
|
|
|
, |
|
|
|
|
||||||
|
2 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
k 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3. Формула Симпсона (формула парабол).
114
|
|
|
b |
f x dx |
b a |
f |
|
|
|
4 f f |
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
0 |
f |
N |
3 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
3N |
|
1 |
|
|
|
|
(6.5) |
||||||||||
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
... fN 1 2 f2 f4 ... fN 2 , |
|
|
|
|
|
|
|
|
|||||||||||||||
число N считается четным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
4. Квадратурная формула Гаусса. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
b |
|
|
|
|
b |
a |
N |
|
|
|
|
|
|
|
|
a b |
|
b a |
|
||||||
|
f x dx |
Hk f xk , |
|
xk |
|
|
tk . |
|||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
a |
|
|
|
|
|
|
2 |
|
k 1 |
|
|
|
|
|
|
|
2 |
2 |
|
||||||
Значения узлов tk и весов Hk |
приведены в таблице. |
(6.8) |
||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||
|
|
Узлы и веса квадратурной формулы Гаусса |
||||||||||||||||||||||||
|
n 1 |
|
|
|
|
|
|
t1 0.5 |
|
|
|
|
|
|
|
H1 2 |
||||||||||
|
n 2 |
|
|
t |
t |
2 |
0.577350269 |
|
H |
|
H |
2 |
2 |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||||
|
n 3 |
|
|
t1 t3 |
0.774596669 |
|
H1 H3 0.555555555 |
|||||||||||||||||||
|
|
|
|
|
|
|
t2 0 |
|
|
|
|
H2 0.888888888 |
||||||||||||||
|
n 4 |
|
t1 t4 |
0.861136311 |
|
H1 H4 0.347854845 |
||||||||||||||||||||
|
|
|
t3 |
t2 |
0.339981043 |
|
H2 H3 0.652145155 |
|||||||||||||||||||
|
n 5 |
|
t1 t5 |
0.906179846 |
|
H1 H5 0.236926885 |
||||||||||||||||||||
|
|
t2 |
t4 |
0.538469310 |
|
H2 H4 0.478628670 |
||||||||||||||||||||
|
|
|
|
|
|
|
t3 0 |
|
|
|
|
H3 0.568888888 |
||||||||||||||
Практические задания
Вычислить численно одним из разобранных методов интегралы от следующих функций на интервале, в котором функции отличны от нуля. Оценить погрешность вычислений. Сравнить полученный результат с найденным аналитически.
115

1. |
f t 51 2 |
|
t |
|
|
|
|
, |
|
|
t |
|
|
|
2; |
|
|
3. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
2. |
f t 4cos 0t |
|
, |
|
|
t |
|
2, |
T 4, |
T 2 0 |
6 . |
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
3. |
f t 2t , 0 t , 4. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
4. |
f t 8exp t2 |
|
2 2 , |
|
|
|
|
|
|
|
t |
|
|
2, |
5. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
5. |
f t 4 1 2t 2 , |
|
t |
|
|
|
2, 3. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
2 |
|
|
|
|
|
t 2, |
|
|
|
|
|
|
|
|
|
2 t 0 |
2; |
|
0 2; |
||||||||||||||||||||||||||||||||||||||||
6. |
f t |
|
|
|
|
|
|
|
0 2, |
|
|
0 2 t 0 |
2; |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
5. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
2 t , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 2 t 2; |
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
7. |
f t 7 sin 2 t |
|
|
|
2 t, |
|
t |
|
|
|
|
|
2, |
2.5. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
f t 6e 4 |
|
t |
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
8. |
|
|
|
t |
|
2, |
6. |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
4 |
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
9. |
f t 8 1 e |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
0 t , 4. |
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
f t 3.3 |
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
10. |
|
1 10t |
|
2 |
|
|
t |
|
|
|
|
2, |
7 . |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
11. |
f t 5.21 t |
|
|
, |
|
|
|
t |
|
2, |
|
|
4, |
T 6. |
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3t 1 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 t 1; |
|
1 3 4; |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
5 t 1 a0 2 |
t |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
12. |
f t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, 1 t 2; |
2 |
3 3 4; |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 1 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 T 2,T; T 6. |
|||||||||||||||||||||||||||
|
|
|
|
5 3 t 3 2 , |
|
|
2 t 3; |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
13. |
f t 5.4 texp 2t2 , |
|
|
|
|
|
|
|
t |
|
T |
2, 1;3, T 6. |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
14. |
f t e t |
|
e t , |
0 t , |
4, |
1, |
3. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
15. |
f t 10cos2 t |
|
, |
|
|
t |
|
, |
5. |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
16. |
f t 4arctg t |
|
1 t2 |
|
|
, |
|
t |
|
; |
/4. |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
116
ЛАБОРАТОРНАЯ РАБОТА № 7
ИНТЕРПОЛИРОВАНИЕ АЛГЕБРАИЧЕСКИМИ МНОГОЧЛЕНАМИ
Цель работы: Изучение приближения функции, заданной в узлах, алгебраическими многочленами; построение интерполяционного многочлена.
Теоретические сведения
Пусть между некими величинами x и y существует функциональная зависимость y=f(x), аналитический вид которой неизвестен. В результате эксперимента получены пары значений xk, fk , fk f xk , k 1..n, n— количество выполненных измерений. Тем самым функция f(x) задана таблицей значений в некоторых точках (узлах интерполирования) отрезка [a,b].
Задача интерполирования заключается в подборе на основе экспериментальных данных функции g(x) в некотором смысле близкой к f(x). Будем искать функцию g(x) в классе алгебраических многочленов вида
g x P (x) = a |
+ a x + a x2 |
+ ... + a xn |
. (7.1) |
||
n |
0 |
1 |
2 |
n |
|
Очевидно функция Pn x полностью определяется коэффици-
ентами ak , k 1..n. Потребуем, чтобы значения многочлена
Pn x совпадали с измеренными значениями функции в узлах интерполяции, в результате получим систему линейных уравнений относительно ak :
117
a |
+ a x |
+ a x2 |
+ ... + a xn |
f , |
|
|
||
|
0 |
1 1 |
2 1 |
n 1 |
1 |
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
+ a x |
+ a x2 |
+ ... + a xn |
f |
|
, |
(7.2) |
a |
k |
|||||||
|
0 |
1 k |
2 k |
n k |
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
+ a x2 |
+ ... + a xn |
|
|
|
|
a |
+ a x |
f |
n |
. |
|
|||
|
0 |
1 n |
2 n |
n n |
|
|
|
|
Решение системы уравнений (7.2) позволяет выразить коэффициенты ak через экспериментальные данные xk, fk , под-
ставив которые в формулу (7.1), можно получить выражение для интерполяционного многочлена. Система уравнений (7.2) имеет единственное решение, которое можно записать различным образом. Широко распространены интерполяционные многочлены в форме Лагранжа и Ньютона.
Интерполяционная формула Лагранжа позволяет пред-
ставить многочлен в виде
n |
(x x0)...(x xk 1)(x xk 1)...(x xn) |
|
||||||||
Pn(x) fk |
|
|||||||||
(x |
x )...(x |
x |
)(x |
x |
)...(x |
x ) |
||||
k 0 |
k |
0 |
k |
k 1 |
k |
k 1 |
k |
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
n |
|
(x xj) |
|
|
|
|
||
|
fk |
j 0,j k |
|
. |
|
|
(7.3) |
|||
|
n |
|
|
|
||||||
|
|
k 0 |
(xk xj) |
|
|
|
|
|||
j 0,j k
Интерполирование по формуле Лагранжа довольно просто реализуется в виде подпрограммы, но имеет существенный недостаток: при добавлении новых узлов интерполяционный многочлен надо строить заново.
Преодолеть указанный недостаток позволяет использование интерполяционной формулы Ньютона. Она выражает
118

многочлен Pn(x) через значение f(x) в одном из узлов и так называемые разделенные разности.
Для построения разделенных разностей будем считать, что среди точек xk нет совпадающих. Разделенными разно-
стями первого порядка называются величины
f (x ,x |
j |
) |
f (xj) f (xi) |
,i, j 0,1,...,n, |
i j. |
|
|||||
i |
|
xj xi |
|
||
|
|
|
|
||
На основе разделенных разностей первого порядка, составленным по соседним узлам f(x0,x1), f(x1,x2),..., f(xn-1,xn), можно построить разделенные разности второго порядка
f (x ,x ,x |
2 |
) |
|
|
|
f (x1,x2) f (x0,x1) |
, |
|
|||
|
|
|
|||||||||
0 |
1 |
|
|
|
|
|
x2 x0 |
||||
|
|
|
|
|
|
|
|
||||
f (x ,x ,x ) |
|
|
|
f (x2,x3) f (x1,x2) |
, |
|
|||||
|
|
|
|||||||||
1 |
2 |
3 |
|
|
|
|
x3 x1 |
||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
... |
|
|
|
||
f (xn 2,xn 1,xn) |
|
|
f (xn 1,xn) f (xn 2,xn 1) |
. |
|||||||
|
|
||||||||||
|
|
|
|
|
|
|
|
xn xn 2 |
|||
Аналогично определяются разделенных разностей более высокого (k+1)-ого порядка по уже известным разностям порядка k:
f(xj,xj 1,...,xj k,xj k 1)
f(xj 1,xj 2,...,xj k 1) f(xj,xj 1,...,xj k)
xj k 1 xj
Использование разделенных разностей позволяет записать интерполяционный многочлен Ньютона для интерполирования вперед (начальной точкой выбрана x0)
Pn(x) f(x0)+ f(x0,x1)(x x0)+ f (x0,x1,x2)(x x0)(x x1)+...+(7.4) + f (x0,x1,...,xn 1,xn)(x x0)(x x1)...(x xn 1)
119
