Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

673

.pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

12.75 Mб

Скачать

☆

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

(x − x′+ 2nL)2

exp

−

n=∞

4at

G (x, x′,t )

∑ (−1)

(x + x′+ 2nL)2

πat n=−∞

+exp

−

4at

∞

(

)

(

)

aπ

2 (

x′

2n +1

∑cos

cos

exp −

L n=1

Первый ряд быстро сходится при малых t, второй – при больших t.

3. Математическое описание некоторых сварочных источников тепла

Математическое описание наиболее распространенных сварочных источников тепла в декартовой системе координат приведено в работе [3]. С некоторыми допущениями все многообразие сварочных источников тепла можно получить, пользуясь мгновенным точечным источником теплоты. Для математического описания мгновенных точечных источников применяется дельта-функция Дирака. Дельта-функция обозначается через δ(x) и обладает следующими свойствами:

–функция равна нулю при всех x < 0 и при всех x > 0;

–функция бесконечна при x = 0;

–интеграл от этой функции, взятый в пределах от – ∞ до ∞, равен 1. Из свойств δ(x) следует основное соотношение:

I = ∞∫ δ(x)f (x)dx = f (0).

−∞

Отметим также, что δ(x–a) отлично от нуля только при x = a, т.е.

I = ∞∫ δ(x − a)f (x)dx = f (a).

−∞

Это свойство будет использовано при описании подвижного источника. Приведем описание некоторых источников.

3.1. Мгновенный неподвижный точечный источник:

F= cqρδ(ϕ′)δ(r′− R)δ(z′)δ(τ).

3.2.Непрерывно действующий неподвижный точечный источник:

F = cqρδ(ϕ′)δ(r′− R)δ(z′)E (τ),

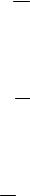
( ) 1 при0 < τ≤ t E τ = 0 приτ> t .

3.3. Непрерывно действующий подвижный (вдоль оси Z) точечный источник (линейная скорость передвижения V):

F= cqρδ(ϕ′)δ(r′− R)δ(z′−V τ)E (τ).

3.4.Непрерывно действующий на наружной поверхности подвижный (по кругу) точечный источник (угловая скорость ω):

F= cqρδ(ϕ′−ωτ)δ(r′− R)δ(z)E (τ).

3.5.Непрерывно действующий подвижный (по спирали) точечный источник (угловая скорость ω, линейная V по оси Z ):

F= cqρδ(ϕ′−ωτ)δ(r′− R)δ(z −V τ)E (τ).

3.6.Непрерывно действующий подвижный (по кругу) линейный источник (вдоль оси Z) величиной h:

F =	q	δ(ϕ′−ωτ)δ(r′− R1 )E (z)E (τ),
F =	cρ	δ(ϕ′−ωτ)δ(r′− R1 )E (z)E (τ),
	cρ
	E (τ) = 1 при 0 ≤ z ≤ h		.
		0 при z < 0, z > h

Данный источник может применяться при сварке с колебаниями поперек шва, при наплавке ленточным электродом, при сварке с глубоким проплавлением.

Приведенное описание подвижных тепловых источников предусматривает систему координат неподвижной. Для того чтобы преобразовать полученное решение в подвижную систему координат, необходимо поменять знак (с минуса на плюс) скорости (угловой или линейной) [5].

4. Разработка модели и исследование тепловых процессов при наплавке сплошных бесконечных цилиндров по образующим

в углекислом газе проволокой диаметром 1,2 мм

Примем, что начальные условия и граничные второго рода равны нулю. Тогда функцию Грина составим из функций пп. 1.2 и 2.1, а тепловой источник – по п. 3.3. Тогда решение в интегральном виде принимает вид:

T (r,ϕ,r,t )=	qη	∫t ∞∫ 2∫π ∫R {	1		+
			πR	2
	cρ 0 −∞ 0 0

+	1	∞ ∞	Anµn2	,m Jn (µn,m r )Jn (µn,m r′)		cos n(ϕ−ϕ′) exp	(	−µ2
		∑∑			2
			(µn2,m R2 − n2 ) Jn (µn,m R)					n,m
	π n=0 m=1

at ) ×

(x − x′)2

exp

−

δ(ϕ′)δ(r′− R)δ(z′−V τ)E (τ)∂r′∂ϕ′∂z′∂τ.

πat

4at

Используя свойства δ(x), приведем окончательное решение:

T (r,ϕ,r,t )=

∫t {

cρ

π R2

∞

∑∑

Anµn,m Jn (µn,m r )Jn (µn,m R)

cos

n(ϕ) exp

(

−µ2

aτ

(µn2,m R2 − n2 ) Jn (µn,m R)

n,m

)

π n=0 m=1

(x +V τ)2

exp

−

dτ,

πat

4aτ

=1, An = 2 (n =1, 2, …),

(1)

где Jn (r′) – функции Бесселя (штрих означает производную по аргументу); µn,m – положительные корни трансцендентного уравнения Jn ′(µn,m R)= 0; η –

коэффициент полезного действия. t0 зависит от коэффициента сосредоточенности источника [5].

Перед расчетом по разработанной модели необходимо составить матрицу положительных корней трансцендентного уравнения:

Jn ′(µn,m R)=	n	Jn (n,µn,m R)− Jn (n +1,µn,m R)= 0.

	µn,m R

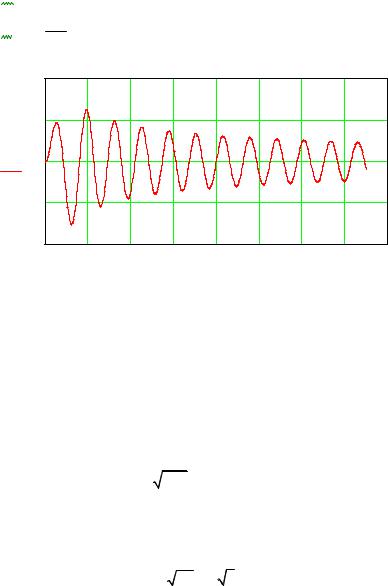
Рассчитать корни этого уравнения можно с помощью математического пакета Mathcad. Для каждой модели трансцендентное уравнение свое, свои радиусы цилиндрических деталей, поэтому каждый раз необходимо составлять матрицы корней. Количество необходимых корней для получения адекватных реальности результатов в каждом случае подбирается. Так, в нашем примере для сплошного цилиндра радиусом 50 мм требуется матрица корней 18×15. На рис. 1 приведен листинг расчета корней в пакете Mathcad. Данный алгоритм предполагает расчет каждого корня отдельно и занесение его в матрицу вручную. Для ускорения расчетов можно с помощью имеющихся в Mathcad средств программирования составить специальную программу, которая бы рассчитывала и заносила корни в матрицу.

R := 0.05 n := 0 .. 20 i := 10 .. 10000 µ i := 0.15 i

		n	Jn(n,µ i R) − Jn(n + 1 ,µ i R)
Fn ,	i := µ i R		Jn(n,µ i R) − Jn(n + 1 ,µ i R)
	0.4
	0.2
F3,i	0
	− 0.2
	− 0.4

0	200	400	600		800	1×103 1.2×103 1.4×103 1.6×103
					µ i
µ1 := 0 .. 10000		F1(µ1 ,n) :=			n	Jn(n,µ1 R) − Jn(n + 1 ,µ1 R)
µ1 := 0 .. 10000		F1(µ1 ,n) :=		µ1 R		Jn(n,µ1 R) − Jn(n + 1 ,µ1 R)
				µ1 R
root(F1(µ1 ,3) ,µ1 ,200 ,260) =			226.918486

Рис. 1. Листинг расчета корней трансцендентного уравнения

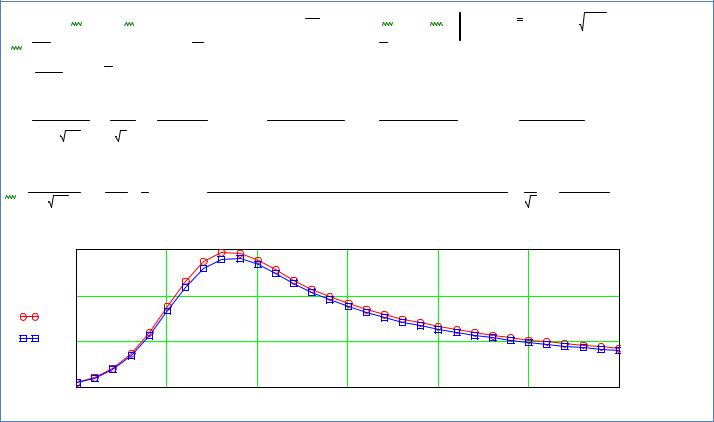
На рис. 2 приведен листинг расчета термического цикла сварки вблизи линии сплавления по модели (1) и построение графика термического цикла. На этом же графике приведена для сравнения вторая кривая, характеризующая термический цикл при наплавке на бесконечный брусок, имеющий в по-

перечном сечении размер L = πR2 . Все исходные данные одинаковы, режимы взяты из работ [6, 7]. Расчет второй кривой производился по следующему уравнению:

T (x, y, z,t )=

qη

(x +V τ)2

∫

exp −

4cρ

(

πa )

4aτ

(y − h + 2nL)2

(2)

exp

−

(

z + 2nL

4aτ

×∑

∑exp

−

dτ.

4aτ

n=−7

(y − h + 2nL)

k =−7

+exp

−

4aτ

n := 0.. 18

m := 0.. 12

c := 600

ρ := 7700

λ := 35

a :=

t := 15

R := 0.05

An :=

A ← 1

if n

π R2

c ρ

L1 :=

I := 130

U := 23

V :=

q := I U

r := R

h := L1

d := 0.003

y := h − d

φ :=

t0 := 0.3

A ← 2

n ≥ 1

i := 0.. 30

z := 0.005 − 0.001 i

3600

t1 :=

0.001 i

ω :=

x := 0.005 − 0.001 i

z1 := 0

η := 0.78

⌠t

−(y − h + 2 n L1)2

−(y + h + 2 n L1)2

−(z1 + 2 m L1)2

T1 :=

q η

−(xi + V τ)

exp

∑

exp

∑

exp

dτ

4 c ρ ( π a)3

(

τ)3

4 a τ

n = − 7

4 a τ

m = − 7

4 a τ

⌡t0

q η

⌠t

−(zi

Jn(n ,µn,m r) Jn(n ,µn,m R) cos [n (φ)] exp −(µn,m)

a τ An (µn,m)

+ V τ)

c ρ ( π a

∑ ∑

(µ

)2 R2

(Jn(n,µ

R))2

exp

dτ

π R2

n = 0 m = 0

− n2

4 a τ

⌡

n,m

1.5×103

1×103

T1i

500

t1i

Рис. 2. Листинг расчета в пакете Mathcad: термические циклы наплавки бруска Ti и сплошного цилиндра T1i

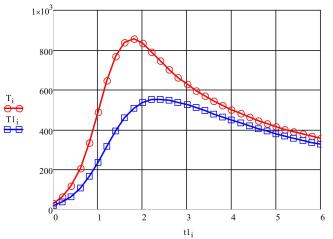
Уравнение (2) получено по методике, изложенной в работе [2]. Сравнение обеих кривых показывает, что они практически совпадают. Интересно, что кривые термических циклов совпадают вблизи линии сплавления и значительно отличаются при увеличении расстояния от шва. На рис. 3 показаны термические циклы точек, находящихся на расстоянии 6 мм от центра шва (ширина шва равна примерно 6 мм). Данное значительное отличие термических циклов показывает важность линейных моделей для цилиндрических тел и невозможность применять известные для полубесконечных тел и пластин формулы с целью оценки распределения температур в цилиндрических телах.

Рис. 3. Графики термических циклов точек, находящихся на расстоянии 6 мм от центра шва (цилиндрическое тело – Ti, брусок – T1i). Графики выполнены в формате Mathcad

Таким образом, показано, что с помощью широко распространенного в математической физике для решения параболических дифференциальных уравнений метода функций Грина можно получить адекватные математические модели распределения температур в цилиндрических деталях.

Статья подготовлена по результатам выполнения работ по гранту РФФИ-Урал (заявка № 11-08-96016, номер государственной регистрации НИР 01201168147), а также в рамках научного проекта, реализуемого международной исследовательской группой ученых на базе ПНИПУ.

Список литературы

1. Махненко В.И., Кравцов Т.Г. Тепловые процессы при механизированной наплавке деталей типа круговых цилиндров. – Киев: Наукова думка, 1976. – 159 с.

2.Язовских В.М. Построение тепловых моделей при сварке методом функций Грина // Вестник ПГТУ. Сварка. – Пермь, 2002. – С. 25–48.

3.Язовских В.М. Математическое моделирование и инженерные методы расчета в сварке: в 2 ч. Ч. 2. Тепловые процессы при сварке и моделирование

впакете Mathcad. – Пермь: Изд-во Перм. гос. техн. ун-та, 2008. – 119 с.

4.Полянин А.Д. Справочник по линейным уравнениям математической физики. – М.: Физматлит, 2001. – 576 с.

5.Рыкалин Н.Н. Расчеты тепловых процессов при сварке. – М.: Машгиз, 1951. – 296 с.

6.Потапьевский А.Г. Сварка в защитных газах плавящимся электродом. – М.: Машиностроение, 1974. – 240 с.

7.Новожилов Н.М. Основы металлургии дуговой сварки в газах. – М.: Машиностроение, 1979. – 231 с.

Получено 1.02.2012

УДК 621.8

В.В. Зелинский

V.V. Zelinskiy

Муромский институт (филиал)

ФГБОУ ВПО «Владимирский государственный университет»

Murom Institute of Vladimir State University

НОВЫЙ ПОДХОД В ТЕОРИИ ПОВЕРХНОСТНОГО УПРОЧНЕНИЯ ВАЛОВ НАКАТЫВАНИЕМ

A NEW APPROACH TO THE THEORY

OF SURFACE HARDENING ROLLING SHAFT

Для поверхностного упрочнения валов накатыванием изучены причины образования дефектов в очаге деформации, на условии отсутствия которых предложена коническая форма накатного ролика, обеспечивающая однородную деформацию. На основе рассмотрения взаимосвязи режимных факторов и введения фактора трения ролика о поверхность проведено математическое моделирование процесса пластического деформирования с использованием теории пластичности. Результаты модельных расчетов показали достаточное соответствие экспериментальным результатам.

Ключевые слова: накатывание, упрочнение, вал, поверхностное упрочнение.

For surface hardening rolling shaft studied the causes of defects in the deformation on the absence of which offered a conical shape rolling roll, providing a homogeneous deformation. Based on consideration of the relationship of regime factors and the introduction of friction factor on the surface of the roller the mathematical modeling of plastic deformation using the theory of plasticity. The results of model calculations have shown substantial conformity with experimental results.

Key words: rolling, hardening, surface hardening, shaft.

При накатывании в зоне контакта тороидального ролика с валом возникает очаг деформации. Традиционно считается, что его размеры и форма определяются радиусом R рабочего профиля ролика и радиальным усилием F прижатия ролика к валу. Однако при рассмотрении процесса деформирования в общей постановке становится ясным, что фактор F не может считаться объективным, так как одно и то же усилие для материалов с разными механическими свойствами вызывает разные деформации и, следовательно, разные размеры и форму очага деформации. Целесообразно за фактор F принять не усилие, а глубину внедрения а ролика в тело вала (величину натяга).

При накатывании перед роликом образуется волна вспучивания. Установлено [1], что разрушения развиваются в ее вершине. При этом образовав-

шаяся наружная трещина закатывается роликом, становясь внутренним дефектом поверхностного слоя. Эта поврежденность частично может залечиваться, но оставшаяся часть будет определять эксплуатационные надежность и долговечность вала.

Анализ условий деформирования поверхностного слоя вала в пределах дуги контакта с роликом показал: а) в осевом сечении деформация вдоль этой дуги неоднородна из-за переменности угла между профилем ролика и валом, б) в касательной плоскости окружные деформации растяжения, обусловливающие появление трещины, из условия постоянства объема при пластическом деформировании вызываются осевыми деформациями сжатия. В связи

сэтим критические деформации растяжения локализуются в вершине волны, как в наиболее ослабленном сечении. Увеличение сечения волны можно обеспечить снижением угла между профилем ролика и поверхностью вала (угла контакта) и его стабилизацией. Такую геометрию волны дает ролик

сконической рабочей поверхностью, который, кроме того, благодаря постоянству угла контакта обеспечивает более однородную деформацию.

При поиске эффективных режимов накатывания традиционно используется эмпирический путь. Однако он не позволяет прогнозировать направление и уровень влияния отдельных факторов, затрудняет раскрытие общих закономерностей формирования параметров упрочнения, не обеспечивает использование ЭВМ для оптимизации технологии накатывания. Поэтому было применено математическое моделирование на основе теории обработки металлов давлением с учетом контактного трения ролика о деталь. Адекватность принятой теоретической модели условиям поверхностного деформирования оценивалась по виду преобладающей деформации, по напряженнодеформированному состоянию, по форме очага деформации.

Принципиально новым для накатывания является учет контактного трения ролика о деталь. Сопротивление сдвигу является общепризнанным параметром локального пластического контакта. При этом локальный пластический контакт находится в условиях комбинированного нагружения нормальной и касательной нагрузками, регламентированного условием пластичности. В соответствии с теорией обработки металлов давлением контактное трение может возбудить на поверхности касательное напряжение τ, достигающее

величины 0,5σs ( σs – истинный предел текучести). Для толщины упрочняемого при накатывании слоя влияние τ такого уровня весьма существенно. Таким образом, трение ролика о деталь является составной частью общей структуры неоднородного деформирования, имеющей частные и общие признаки (законы трения и напряженно-деформированное состояние). При этом условия трения не являются граничными, они возникают по законам самоорганизации [2].

При решении практических задач по накатыванию возникают трудности, связанные с учетом объемности напряженно-деформированного состояния. Решения становятся настолько громоздкими, что теряют свою инженерную ценность. С достаточным для практики приближением при накатывании валов можно принять плоское деформированное состояние, а материал считать жесткопластическим (упругие деформации отсутствуют). Для выбора плоскости деформирования имеется ряд косвенных признаков. Прежде всего, к ним относятся результаты экспериментальных исследований процесса накатывания [3] (проведенные в ЦНИИ МПС и ставшие классическими), показавшие, что осевые напряжения являются наибольшими, а радиальные – наименьшими. Аналогичные выводы делаются в работе [1].

С учетом изложенного процесс накатывания моделировался взаимодействием конического индентора с жесткопластическим полупространством. Индентор, нагруженный нормальной и касательной нагрузками, перемещается в условиях пластического вдавливания и внедрен в полупространство на величину а. Образующая конического индентора составляет с границей полупространства угол контакта β. Пластическая деформация, вызванная ин-

дентором, распространяется на глубину h. Вдоль контактной поверхности действует удельная сила трения. Применялось условие пластичности Треска.

В расчетах использовался метод баланса работ внешних и внутренних сил для очага деформации [4, 5], предполагающий отсутствие влияния касательной силы на распределение главных напряжений, но учитывающий возможность изменения механических свойств материала (упрочнение).

Для учета процесса упрочнения в моделировании использовалась опытная кривая упрочнения для стали 40Х [5]. Анализ кривой упрочнения показал, что в исследуемом диапазоне относительных деформаций для нее характерно пологое повышение предела текучести. Поэтому с достаточной точностью зависимость предела текучести σs от относительной деформации мож-

но линеаризировать и представить в виде

σs =σ0 +П0ε,

где σ0 – экстраполированный предел текучести при отсутствии деформации; П0 – модуль упрочнения; ε – относительная деформация.

При введении соответствующих обозначений данное уравнение приводится к уравнению в относительной форме:

ϕ=Пε,

где ϕ – относительная степень упрочнения; П – относительный модуль упрочнения.

<<< < Предыдущая 12 / 132 3 4 5 6 7 8 9 10 11 12 13 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.202212.62 Mб4667.pdf
#
15.11.20223.42 Mб5668.pdf
#
15.11.20227.22 Mб1669.pdf
#
15.11.20221.35 Mб0671.pdf
#
15.11.20221.16 Mб0672.pdf
#
15.11.202212.75 Mб1673.pdf
#
15.11.20223.46 Mб9674.pdf
#
15.11.20226.65 Mб5675.pdf
#
15.11.20223.48 Mб0677.pdf
#
15.11.20223.48 Mб0678.pdf
#
15.11.202215.43 Mб1681.pdf