368

например SYSWELD французской фирмы ESI Group или LaserCAD Института лазерных и сварочных технологий СПбГПУ [23, 58, 125]. Недостатком этих пакетов является отсутствие возможности решения обратной задачи теплопроводности применительно к термообработке.

3.3.Обратная задача теплопроводности

иметоды ее решения

Использование оптимального управления связано с применением математических моделей тепловых процессов. При этом должна решаться обратная задача теплопроводности: для заданного значения температуры должны быть определены параметры источника энергии. Решение обратной задачи, в отличие от прямой, где осуществляется расчет температуры по известным параметрам источника, неоднозначно, то есть существует несколько множеств значений мощности, скорости и размеров источника, способных обеспечить одно и то же заданное значение температуры. Как правило, исходные данные в обратной задаче теплопроводности применительно к сварке – геометрические размеры шва.

Вариационные методы являются наиболее общими в теории оптимального управления, они могут быть использованы при поиске экстремума нелинейных функционалов с нелинейными уравнениями связей. В случае нелинейных систем принцип максимума не имеет преимуществ перед методами вариационного исчисления, которые в этом случае могут оказаться проще и нагляднее.

Рассмотрим постановку и решение задач оптимизации с использованием схем мгновенного и быстродвижущегося точечного и линейного мгновенного источников, введенных Н.Н. Рыкалиным при создании теории тепловых процессов сварки.

Мгновенные сосредоточенные источники являются моделями, построенными на основе принципа местного влияния в пространстве и во времени. Сосредоточенные в пространстве источники (точечные, линейные, плоские) являются идеализацией, которая по принципу местного влияния возможна при ис-

81

следовании теплового процесса в точках, удаленных от области воздействия на два-три характерных размера (например, размера пятна нагрева).

3.3.1. Оптимизация теплового процесса при воздействии мгновенного точечного источника

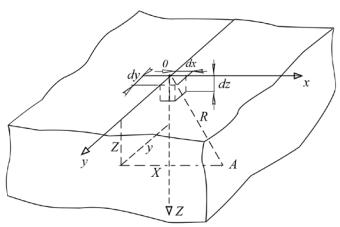
Рассмотрим тепловой процесс в полубесконечном теле при воздействии мгновенного источника у поверхности тела в эле-

Пусть в точку О в начальный момент времени введено количество тепла Q . Температуру тела в начальный момент принима-

ем равной нулю. Граница тела Oxy не пропускает тепла, то есть

при z = 0 градиент ∂T / ∂z = 0 . Процесс распространения тепла источника Q, приложенного у не пропускающей тепло граничной плоскости полубесконечного тела, эквивалентен процессу распространения тепла 2Q в бесконечном теле [7].

Рис. 3.1. Схема полубесконечного тела с мгновенным источником в элементарном объеме dx dy dz

82

Уравнение пространственного процесса выравнивания тепла, внесенного в начальный момент времени в точку О на поверхности полубесконечного тела, имеет вид

Уравнение (3.1) определяет изменение температуры в произвольно выбранной точке А в зависимости от времени t и пространственных координат x, y, z точки, связанных соотношени-

ем R2 = x2 + y2 + z2 . Все точки в полусфере с постоянным ра-

диусом R имеют в данный момент одинаковую температуру, то есть температурное поле в полубесконечном теле симметрично относительно точки О приложения источника. Изотермическими поверхностями являются полусферы с центром О.

Анализ уравнения (3.1), распределение температуры по радиусу в различные моменты времени и изменение температуры в различных точках во времени приведеныв монографии [7].

Рассмотрим задачу оптимизации энергии мгновенного точечного источника. Пусть задано распределение температуры вдоль радиуса (рис. 3.2)

Такое распределение определяет зону нагрева до некоторой температуры Tm , например до температуры плавления, вдоль

радиуса от 0 до R' и зону R ≥ R' , в которой нагрев не требуется. Очевидно, что это заданное распределение температуры (3.2) является идеализацией, но его можно использовать в качестве желаемого распределения вдоль радиуса при постановке следую-

щей задачи оптимизации: найти энергию Q мгновенного точечного источника у поверхности полубесконечного тела, при

83

которой в момент времени t' после воздействия мгновенного источника обеспечивается минимальное уклонение истинной температуры T (R,t ') от заданной T '(R) . Максимальное значе-

ние энергии Q неограниченно.

Решение задачи получим путем минимизации функционала, составленного на невязках уравнения (3.1). Если в правую часть уравнения (3.1) вместо T (R,t) подставить T '(R) , то раз-

ность левой и правой части для момента времени t' является невязкой этого уравнения:

или в форме сокращенной записи

T '(R) −T (R,t ') .

Составим квадратичный функционал невязок на промежутке t':

Квадрат невязки позволяет устранить зависимость подынтегральной функции от знака невязки, величина которой может быть как положительной, так и отрицательной (см. рис. 3.2, заштрихованная область).

Минимум функционала (3.3) по Q позволяет найти величину Q , при которой обеспечивается минимальное уклонение температуры T (R,t ') в момент времени t' от заданного T '(R) .

84

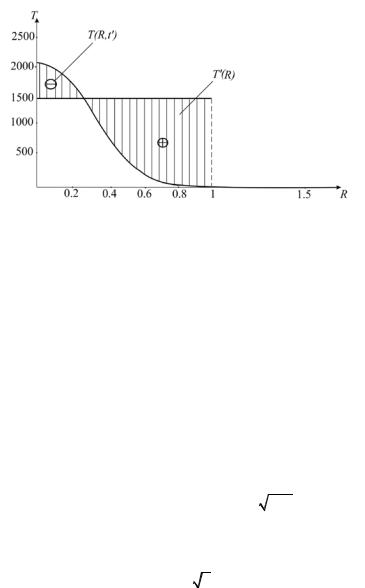
Рис. 3.2. Заданное распределение температуры T '(R) и истинное T (R,t ') : (+) – положительный знак невязки; (–) – отрицательный знак невязки

Подставим выражения (3.1) и ( 3.2) в подынтегральную функцию (3.3) и выполним преобразование функционала:

R ' R ' ∞

J[Q] = ∫Tm2dR −2∫TmT (R,t ')dR + ∫T 2 (R,t ')dR =C − BQ + AQ2 ,

Несобственный интеграл в выражении коэффициента А приводится к интегралу Пуассона

Преобразуем и вычислим интеграл:

85

Необходимое условие минимума функционала сводится к условию экстремума параболической функции

2AQ − B = 0 .

Из условия экстремума получаем энергию оптимального мгновенного точечного источника:

Определим энергию оптимального точечного источника при воздействии его на полубесконечное тело в начальный момент времени. Материал полубесконечного тела – сталь 30ХГСА. Значения необходимых для расчета теплофизических характеристик принимаем при температуре 500 ºС:

Tm =1500 0С, R' =1см мгновенный точечный источник, обладающий энергией Qопт =1590 Дж, обеспечивает в момент времени t'=0,5с распределение температуры T (R,t ') , наиболее близкое к заданному T '(R) (см. рис. 3.2).

3.3.2. Оптимизация мощности линейного быстродвижущегося источника нагрева тонкой пластины

Мощный быстродвижущийся источник является частным случаем непрерывно действующих источников, который используется при моделировании упрощенного теплового процесса. При перемещении источника с большой скоростью рассматривают случай предельного состояния, когда V → ∞. В этом случае предполагают, что энергия источника выделяется одновременно вдоль линии перемещения источника, а тепло распространяется в основном в направлении, перпендикулярном оси перемещения источника.

86

Рассмотрим тепловой процесс при стыковой сварке пластин быстродвижущимся источником, равномерно распределенным по толщине. Процесс распространения тепла мощного линейного быстродвижущегося источника в тонкой пластине определяется уравнением [7,16]

где t – время, отсчитываемое от момента, когда источник пересекает ось 0y (см. рис. 3.1), V – скорость перемещения источника в направлении оси x.

В теории сварочных процессов актуальной является задача определения мощности q сварочного источника в зависимости от заданного распределения температуры T '. Функцию заданной температуры с равномерным распределением её максимального значения Tm на отрезке от y1 до y2 оси y определим выражением

Рассмотрим задачу: определить мощность q0 быстродвижущегося источника, при которой в момент времени t' истинное распределение температуры (3.5) имеет минимальное уклонение от заданного (3.6) [17].

Очевидно, что ни при каких значениях q0 температура T (y,t ') не будет точно совпадать с заданным T '(y) . Используя

это условие, построим функционал на невязках уравнения (3.5), если в левой части этого уравнения подставить выражение T '(y) . Квадратичный функционал в этом случае имеет вид

J[q0 ] = ∞∫(T '(y) −T (y,t '))2 dy .

−∞

87

После подстановки выражений (3.5.), (3.6.) и преобразований квадратичный функционал принимает вид

Окончательно функционал сводится к выражению параболической функции от q0 :

C = (Tm )2 (y2 − y1 ) .

Несобственный интеграл в (3.8) можно привести к вычислению интеграла Пуассона

∞∫e−α2 dα = π. −∞

Преобразуем и вычислим несобственный интеграл:

В выражении (3.9) значение интеграла определяется чис-

ленно с использованием MathCAD 2000 Professional.

Оптимальное значение мощности источника q0 определяется при минимальном значении J (q0 ) . Из необходимого условия минимума функции

2Aq – B = 0

получаем выражение оптимальной мощности источника при нагреве тонкой пластины

88

где α = y / 4at ' , α1 = y1 / 4at ' , α2 = y2 / 4at ' .

Подставляем полученное значение мощности линейного быстродвижущегося источника в уравнение (3.5) и вычисляем распределение температуры T (y,t ') в сечении тонкой пластины

вдоль оси y . Это распределение температуры в момент времени t' от источника мощностью q0опт , величина которой опреде-

лена по формуле (3.10), имеет минимальное уклонение от заданного (3.6).

При λ=0,35 Дж/(см/с·°C), a = 0,07 см2/с, δ = 0,1 см, cv = = 5,2 Дж/(см3·°C), t`=1 с, y1 = – 0,5 см, y2=0,5 см, Tm =1500 °С,

V =1 см/с значение мощности линейного источника q0опт по

выражению (3.10) равно 830 Вт.

Заданное и истинное распределения температуры при воздействии этого источника изображены на рис. 3.3. Полученное значение эффективной мощности быстродвижущегося линейного источника при нагреве тонкой пластины является оптимальным в смысле минимального уклонения истинного распределения тем-

пературы T (y,t ') от заданного T '(y) в момент времени t'.

Рис. 3.3. Схема тонкой пластины с заданным 1 и истинным 2 распределениями температуры вдоль оси y

89

По уравнению (3.5) можно определить распределение температуры от q0опт в любой момент времени t , построить термические циклы в точках оси y и выбрать режимы сварочного

источника, например напряжение и ток при электродуговой сварке пластин.

3.3.3. Принцип максимума

Рассмотрим формулировку принципа максимума и его применение на примере решения задачи оптимального управления движением материальной точки. Изложение доказательства принципа максимума приводится в монографии [5] и учебнике [10].

Для определения наименьшего значения функционала составляется функция H, которая в вариационном исчислении называется гамильтонианом.

Рассмотрим частный случай функционала, когда f 0 (x1 , x2 ,..., xn ,u) ≡1. Этот частный случай имеет важное зна-

чение в теории оптимального управления, он определяет боль-

шой класс задач об оптимальном быстродействии. Функцио-

нал в этом случае принимает вид

t0

Для задачи об оптимальном быстродействии гамильтониан имеет вид

α=1

где x(t) = (x1 , x2 ,..., xn ) – радиус-вектор точки в фазовом пространстве; ψ(t) = (ψ1,ψ2 ,...,ψn ) – вектор сопряженных переменных. Сопряженные переменные ψi (t)(i =1,2,...,n) определяются из вспомогательных уравнений