6. Цепи синусоидального тока с резисторами, конденсаторами и катушками индуктивности

Эксперименты данного раздела касаются взаимодействия резисторов, конденсаторов и катушек индуктивности при переменном синусоидальном напряжении.

Цель состоит в измерении и расчете токов, напряжений и их фазовых сдвигов, также как и эквивалентных параметров цепей при параллельном и последовательном соединении резисторов, конденсаторов и катушек.

Действующие значения и фазы соответствующих величин могут быть показаны на векторных диаграммах или на осциллограммах.

На векторной диаграмме каждая синусоидальная функция времени (ток или напряжение) представляется вектором, длина которого соответствует в выбранном масштабе амплитуде или действующему значению, а направление определяется начальной фазой, отсчитываемой от выбранного начала отсчета углов. Например, напряжение u = U_m sin (t+) изображается вектором длинойU_mилиU_m/2, расположенным под угломк горизонтали. Векторные изображения синусоидальных величин в дальнейшем будут подчеркиваться.

6.1. Последовательное соединение резистора и конденсатора

6.1.1. Общие сведения

Когда к цепи (рис. 6.1.1) с последовательным соединением резистора и конденсатора подается переменное синусоидальное напряжение, один и тот же синусоидальный ток имеет место в обоих компонентах цепи.

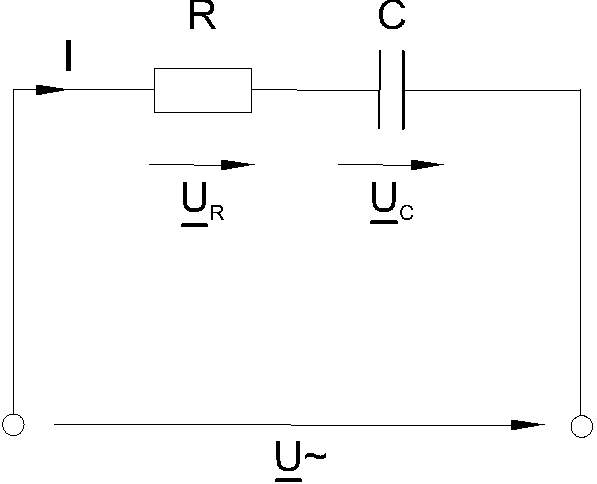
Рис. 6.1.1

Между напряжениями U_R, U_C иU существуют фазовые сдвиги, обусловленные емкостным реактивным сопротивлениемX_Cконденсатора. Они могут быть представлены с помощью векторной диаграммы напряжений (рис. 6.1.2

Рис. 6.1.2

Фазовый сдвиг между током I и напряжением на резистореU_R отсутствует, тогда как сдвиг между этим током и падением напряжения на конденсатореU_Cравен -90⁰ (т.е. ток опережает напряжение на 90⁰). При этом сдвиг между полным напряжением цепиU и токомIопределяется соотношением между сопротивлениями X_CиR.

Если каждую сторону треугольника напряжений разделить на ток, то получим треугольник сопротивлений (рис.6.1.13). В треугольнике сопротивлений Zпредставляет собой так называемое полное сопротивление цепи.

Рис. 6.1.3

Из-за фазового сдвига между током и напряжением в цепях, подобных данной, простое арифметическое сложение действующих или амплитудных значений напряжений на отдельных элементах цепи невозможно. Невозможно и сложение разнородных (активных и реактивных) сопротивлений. Однако, в векторной форме

U = U_R +U_C.

Действующее значение полного напряжения цепи, как следует из векторной диаграммы

= Z  I

Полное сопротивление цепи

= U  I

Активное сопротивление цепи

R = Z  cos 

Емкостное реактивное сопротивление цепи

X_C = Z  sin 

Угол сдвига фаз

 = arctg (-U_C  U_R) = arctg (-Х_C  R)

6.1.2. Экспериментальная часть Задание

Для цепи с последовательным соединением резистора и конденсатора измерьте и вычислите действующие значения падений напряжения на резисторе U_Rи конденсатореU_C, токI, угол сдвига фаз, полное сопротивление цепиZи емкостное реактивное сопротивлениеX_Cи активной сопротивлениеR.

Порядок выполнения работы

• Соберите цепь согласно схеме (рис. 6.1.4), подсоедините регулируемый источник синусоидального напряжения и установите его параметры: U= 5 В,f= 1 кГц.

Рис. 6.1.4

• Выполните мультиметрами или виртуальными приборами измерения действующих значений тока и напряжений, указанных в табл. 6.1.1. При измерениях напряжений подключайте мультиметр или канал V0 коннектора к зажимамC-E,C-D,D-E:

Таблица 6.1.1.

U,B	UR, B	UC, B	I, мА	, град	R, Ом	XC, Ом	Z, Ом	Примечание
								Расчет
								Вирт. Изм

• Вычислите:

Фазовый угол

 = arctg (U_C  U_R) =

Полное сопротивление цепи

Z = U  I =

Активное сопротивление цепи

R = Z cos 

Емкостное реактивное сопротивление цепи

X_C = Z sin 

• Если вы работаете с виртуальными приборами, то измерьте с помощью блока «Приборы II»R, , X_C, Z и запишите их значения также в таблицу 6.1.1 под рассчитанными величинами. Сравните результаты.

• Выберите масштабы и постройте векторную диаграмму напряжений (рис. 6.1.5) и треугольник сопротивлений (рис. 6.1.6).

Рис. 6.1.5 Рис. 6.1.6