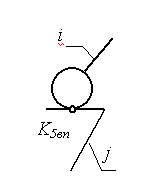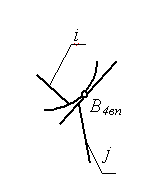- •Введение. Машина и механизм. Подвижность механизма.
- •Введение.
- •Рекомендуемая основная литература:
- •Рекомендуемая дополнительная литература:
- •Цель и задачи курса.
- •Краткая историческая справка
- •Основные разделы курса тмм
- •Машины и их классификация.
- •Понятие о машинном агрегате.
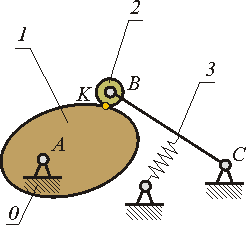
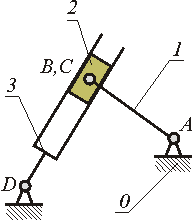
- •Механизм и его элементы.
- •Типы звеньев рычажных механизмов.
- •Классификация кинематических пар.
- •Классификация кинематических пар по числу связей и по подвижности.
- •Подвижность механизма.
Типы звеньев рычажных механизмов.
Стойка– неподвижное звено, относительно которого рассматриваются движения остальных звеньев. На схеме механизма обозначается 0.
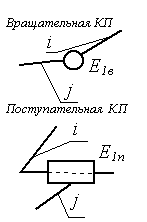
Кривошип– звено, имеющее вращательную КП со стойкой и совершающее полный оборот вокруг неподвижной оси.
Коромысло– звено, имеющее вращательную КП со стойкой и совершающее не полный оборот вокруг неподвижной оси.
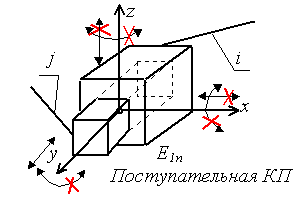
Ползун, штанга– звено, имеющее поступательную КП со стойкой, совершающее поступательное прямолинейное движение.
Шатун – звено, не имеющее КП со стойкой.
Камень– звено небольшого размера, скользящее по подвижной направляющей.
Кулиса– звено, по которому скользит камень, может быть кривошипом, коромыслом, штангой, шатуном.
Кулачок– звено, имеющее профиль переменной кривизны (может быть эксцентрик – диск, вращающийся вокруг оси, не проходящей через центр диска).
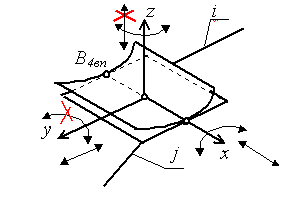
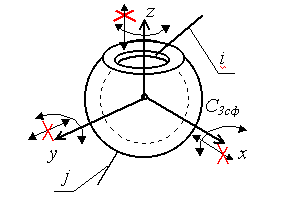
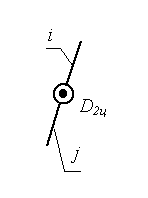
Классификация кинематических пар.
Кинематические пары (КП) классифицируются по следующим признакам:
по виду места контакта (места связи) поверхностей звеньев:
низшие, в которых контакт звеньев осуществляется по плоскости или поверхности (пары скольжения);
высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием).
по относительному движению звеньев, образующих пару:
вращательные;
поступательные;
винтовые;
плоские;
сферические.
по способу замыкания (обеспечения контакта звеньев пары):
силовое (за счет действия сил веса или силы упругости пружины);
геометрическое (за счет конструкции рабочих поверхностей пары).
|
|
|
|
Рис. 1.1 |
Рис. 1.2 |
по числу условий связи, накладываемых на относительное движение звеньев (число условий связи определяет класс кинематической пары);
по числу подвижностей в относительном движении звеньев.
Классификация КП по числу подвижностей и по числу связей приведена в таблице.
Примечание: Стрелки у координатных осей показывают возможные угловые и линейные относительные перемещения звеньев. Если стрелка перечеркнута, то данное движение в КП запрещено (т.е. на данное относительное движение наложена связь).
Классификация кинематических пар по числу связей и по подвижности.
|
Класс пары |
Число связей |
Подвижность |
Пространственная схема (пример) |
Условные обозначения |
|
I |
1 |
5 |
|
|
|
II |
2 |
4 |
|
|
|
III |
3 |
3 |
|
|
|
IV |
4 |
2 |
|
|
|
V |
5 |
1 |
|
|
Подвижность механизма.
Обобщенные координаты механизма.
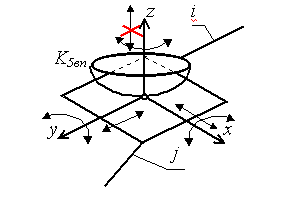
Положение твердого тела, свободно движущегося в пространстве, полностью определяется шестью независимыми координатами, за которые можно принять три координаты начала подвижной системы координат, связанной с телом, и три угла Эйлера, определяющие расположение осей подвижной системы координат относительно неподвижной. Их принято называть обобщенными, так как они определяют положение всего твердого тела. Аналогично обобщенными координатами механизма называют независимые между собой координаты, определяющие положения всех звеньев механизма относительно стойки.
Число степеней свободы механизма.
В механизмах с голономными связями число степеней свободы механизма, т. е. число независимых возможных перемещений, совпадает с числом обобщенных координат. Это утверждение следует из того, что в механизмах с голономными связями уравнения связей содержат только координаты звеньев.
Для определения числа степеней свободы механизма с голономными связями достаточно найти общее число координат, определяющих положения всех звеньев механизма, и число уравнений, связывающих эти координаты. Разность между этими числами дает число независимых координат, если все уравнения связи независимы, т. е. ни одно из них не может быть получено как следствие других.
Пространственный механизм.
Пусть механизм состоит из nподвижных звеньев, соединенных между собой кинематическими парами, число которых соответственно:
pI- число кинематических парIкласса (пятиподвижных),pII- число кинематических парIIкласса (четырехподвижных), и т.д.pV – число кинематических парVкласса (одноподвижных)
Тогда число связей, накладываемых всеми классами кинематических пар на механизм:
S=5 pV+4 pIV+3 pIII+2 pII+1 pI
Общее число координат, определяющих положение nподвижных звеньев механизма, равно
H=6n,
Подвижность механизма определиться
W = H- S=6n-(5 pV+4 pIV+3 pIII+2 pII+1 pI)
W =6n -5 pV-4 pIV-3 pIII-2 pII-1 pI
Для пространственного механизма эта формула носит название формула Сомова-Малышева.
Плоский механизм.
На плоскости H=3, при этом каждая одноподвижная пара накладывает 2 связи, двухподвижная – одну. К пятому классу на плоскости относятся высшие пары, к четвертому – низшие. Таким образом, формула преобразуется к виду:
W = 3n - 2 pн – pв,
Для плоского механизма эта формула носит название формулы Чебышева.