Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Сибирский Государственный Университет Путей Сообщения

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

m0947

.pdf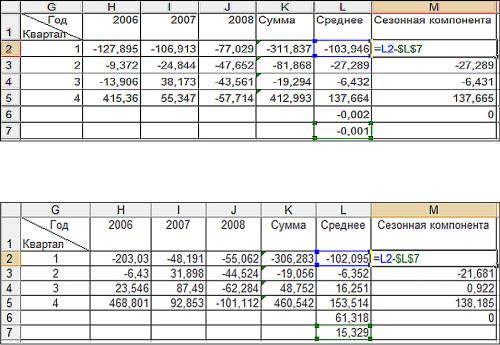

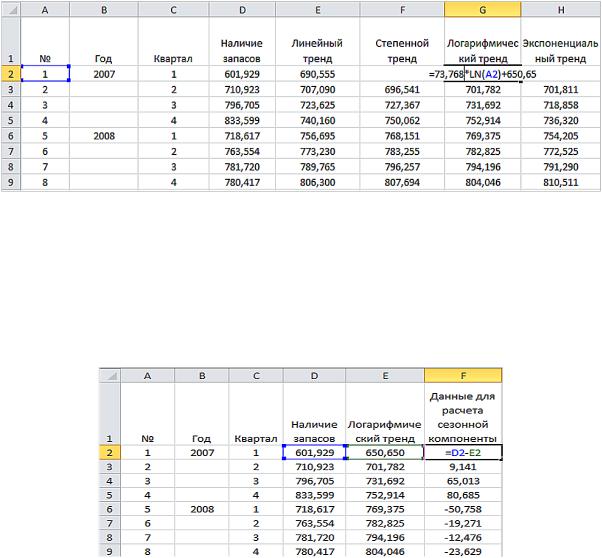
Скачиваний:

Добавлен:

15.11.2022

Размер:

2.82 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Рис. 11. Расчет сезонной компоненты для модели с логарифмическим трендом

Рис. 12. Расчет сезонной компоненты для модели с экспоненциальным трендом

Сезонная компонента: G2 = F2 – $F$7.

Среднее: F2 = (B2 + C2 + D2)/3; F6 = F2 + F3 + F4 + F5; F7 = F6/4.

Сезонная компонента: M2 = L2 – $L$7.

Среднее: L2 = (H2 + I2 + K2)/3; L6 = L2 + L3 + L4 + L5; L7 = L6/4.

Получив четыре сезонных компоненты S с пятью уравнениями тренда T, делаем расчет значения ошибок моделей на основе критерия среднеквадратического отклонения (СКО) E. Расчеты сводятся в таблицу, состоящую из девяти столбцов. В первом указан номер, во втором – год, в третьем – квартал, в четвертом – наличие производственных запасов, в пятом – значение полиномиальной модели (значение полиномиального тренда T + сезонная компонента S). В шестом столбце рассчитываем отклонение значений полиномиальной модели от наличия запасов (разница между значениями 5-го и 4-го столбцов) (рис. 13). В седьмом – отклонение полиномиальной модели от наличия производственных запасов в квадрате (значение столбца 6 в квадрате). В следующем столбце определяем значение полиномиальной модели в квадрате (значение столбца 5 в квадрате) (см. рис. 13). В последнем столбце определяется значение ошибки. Для этого отдельно рассчитывается процент ошибки как отношение суммы отклонений значений модели от запасов в квадрате к сумме

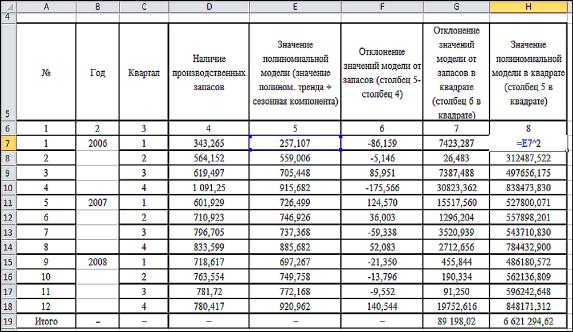
значений полиномиальной модели в квадрате: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %. Затем находится значение ошибки для каждого квартала – берем процент ошибки от количества производственных запасов: столбец 4 ∙ процент ошибки / 100 % (табл. 3).

Рис. 13. Расчет значения полиномиальной модели в квадрате

							Таблица 3
	Расчет прогноза запасов на 2009 г. (полиномиальный тренд)

				Значение	Отклонение	Отклонение	Значение
				полиномиальной	Отклонение	значений	Значение	Значение ошибки
		Квартал	Наличие	полиномиальной	значений	значений	полиномиальной
			Наличие	модели	значений	модели	полиномиальной
			запасов	модели	(столбец 5 –	модели	(столбец 5
№	Год		производ-	(значение	модели	от запасов	модели
			ственных	полиноминального	от запасов	в квадрате	в квадрате
				полиноминального		в квадрате
				тренда + сезонная	– столбец 4)	(столбец 6	в квадрате)
				компонента)	– столбец 4)	в квадрате)	в квадрате)
				компонента)		в квадрате)
1	2	3	4	5	6	7	8	9
1	2006	1	343,265	257,107	-86,159	7 423,287	66 103,752	4,624
2		2	564,152	559,006	-5,146	26,483	312 487,522	7,600
3		3	619,497	705,448	85,951	7 387,488	497 656,175	8,345
4		4	1 091,25	915,682	-175,566	30 823,362	838 473,830	14,701
5	2007	1	601,929	726,499	124,570	15 517,560	527 800,071	8,109
6		2	710,923	746,926	36,003	1 296,204	557 898,201	9,577
7		3	796,705	737,368	-59,338	3 520,939	543 710,830	10,733
8		4	833,599	885,682	52,083	2 712,656	784 432,900	11,230
5	2007	1	601,929	726,499	124,570	15 517,560	527 800,071	8,109
6		2	710,923	746,926	36,003	1 296,204	557 898,201	9,577
7		3	796,705	737,368	-59,338	3 520,939	543 710,830	10,733
8		4	833,599	885,682	52,083	2 712,656	784 432,900	11,230
9	2008	1	718,617	697,267	-21,350	455,844	486 180,572	9,681
10		2	763,554	749,758	-13,796	190,334	562 136,809	10,286
11		3	781,72	772,168	-9,552	91,250	596 242,648	10,531
12		4	780,417	920,962	140,544	19 752,616	848 171,312	10,513
Итого						89 198,02	6 621 294,62	−
Ошибка: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %								1,347

Аналогично рассчитываем ошибки моделей с линейным, степенным, логарифмическим, экспоненциальным трендами в табл. 4–7. На следующем этапе рассчитаем СКО для каждого из периодов.

							Таблица 4
			Расчет прогноза запасов на 2009 г. (линейный тренд)

		Квартал	Наличие производственных запасов	Значение		Отклонение		ошибкиЗначение
		Квартал	Наличие производственных запасов	линейной	Отклонение		Значение	ошибкиЗначение

						значений
				модели	значений	значений	линейной
				модели	значений	модели от	линейной
				(значение	модели	модели от	модели в
№	Год			(значение	модели	запасов	модели в
№	Год			линейного	от запасов	запасов	квадрате
				линейного	от запасов	в квадрате	квадрате
				тренда +	(столбец 5 –	в квадрате	(столбец 5
				тренда +	(столбец 5 –	столбец 6	(столбец 5
				+ сезонная	– столбец 4)	столбец 6	в квадрате)
				+ сезонная	– столбец 4)	в квадрате)	в квадрате)
				компонента)		в квадрате)
				компонента)

1	2	3	4	5	6	7	8	9
1	2006	1	343,265	460,968	117,703	13 853,996	212 491,497	8,549
2		2	564,152	585,907	21,755	473,295	343 287,403	14,050
3		3	619,497	639,005	19,508	380,562	408 327,390	15,428
4		4	1 091,25	808,120	-283,128	80 161,653	653 057,396	27,176
5	2007	1	601,929	554,568	-47,361	2 243,064	307 545,667	14,990
6		2	710,923	679,507	-31,416	986,944	461 730,216	17,705
7		3	796,705	732,605	-64,100	4 108,810	536 710,086	19,841
8		4	833,599	901,720	68,121	4 640,425	813 098,357	20,760
9	2008	1	718,617	648,168	-70,449	4 963,062	420 121,756	17,896
10		2	763,554	773,107	9,553	91,266	597 694,949	19,015
11		3	781,72	826,205	44,485	1 978,915	682 614,702	19,468
12		4	780,417	995,320	214,903	46 183,156	990 661,239	19,435
Итого						160 065,15	6 427 340,66	−
Ошибка: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %								2,490

								Таблица 5
			Расчет прогноза запасов на 2009 г. (степенной тренд)

		Квартал		Наличие производственных запасов	компонента)		в квадрате)		Значениеошибки
					Значение	Отклонение	Отклонение	Значение
					степенной	значений	значений	степенной
					модели	модели	модели	модели в
№	Год				(значение	модели	от запасов	модели в
№	Год				(значение	от запасов	от запасов	квадрате
					степенного тренда +	от запасов	в квадрате	квадрате
					степенного тренда +	(столбец 5 –	в квадрате	(столбец 5
					+ сезонная	(столбец 5 –	(столбец 6	(столбец 5
					+ сезонная	– столбец 4)	(столбец 6	в квадрате)
						– столбец 4)		в квадрате)

1	2	3		4	5	6	7	8	9
1	2006	1		343,265	343,599	0,334	0,111	118060,038	8,949
2		2		564,152	510,017	-54,135	2930,581	260117,503	14,708
3		3		619,497	586,918	-32,579	1061,376	344473,006	16,151
4		4		1 091,25	772,217	-319,031	101780,842	596318,942	28,450
5	2007	1		601,929	584,218	-17,711	313,668	341311,055	15,693
6		2		710,923	694,098	-16,825	283,072	481772,396	18,535
7		3		796,705	739,804	-56,901	3237,741	547309,729	20,771
8		4		833,599	904,510	70,911	5028,431	818139,117	21,733
9	2008	1		718,617	701,639	-16,978	288,263	492296,833	18,735
10		2		763,554	800,158	36,604	1339,871	640253,213	19,907
11		3		781,72	836,845	55,125	3038,721	700308,870	20,380
12		4		780,417	994,183	213,766	45696,045	988400,501	20,346
Итого							164 998,72	6 328 761,20	−
Ошибка: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %									2,607

												Таблица 6
		Расчет прогноза запасов на 2009 г. (логарифмический тренд)

							Значение	Отклонение		Отклонение		Значение
							логарифмической	Отклонение		значений		Значение	Значение ошибки
			Квартал		Наличие		логарифмической	значений		значений		логарифмической
					Наличие		модели	значений		модели		логарифмической
					запасов		модели	(столбец 5 –		модели		(столбец 5
№	Год				производ-		(значение	модели		от запасов		модели
					ственных		логарифмического	от запасов		в квадрате		в квадрате
							логарифмического			в квадрате
							тренда + сезонная	– столбец 4)		(столбец 6		в квадрате)
							компонента)	– столбец 4)		в квадрате)		в квадрате)
							компонента)			в квадрате)

1	2	3		4			5	6	7			8	9
1	2006	1		343,265			367,215	23,950	573,587			134 846,622	6,760
2		2		564,152			546,235	-17,917	321,018			298 372,714	11,110
3		3		619,497			626,972	7,475	55,875			393 093,847	12,200
4		4		1 091,25			813,553	-277,695	77 114,343			661 868,983	21,490
5	2007	1		601,929			604,896	2,967	8,806			365 899,742	11,854
6		2		710,923			708,478	-2,445	5,978			501 941,215	14,000
7		3		796,705			752,101	-44,604	1 989,524			565 655,786	15,689
8		4		833,599			915,917	82,318	6 776,300			838 904,468	16,416
9	2008	1		718,617			691,701	-26,916	724,481			478 450,006	14,152
10		2		763,554			783,917	20,363	414,645			614 525,590	15,037
11		3		781,72			818,850	37,130	1 378,643			670 515,450	15,394
12		4		780,417			975,796	195,379	38 173,098			952 178,555	15,369
Итого									127 536,30			6 476 252,98	−
Ошибка: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %													1,969
												Таблица 7
	Расчет прогноза запасов на 2009 г. (экспоненциальный тренд)

							Значение	Отклонение		Отклонение		Значение
						экспоненциальной		Отклонение		значений		Значение	Значение ошибки
			Квартал		Наличие	экспоненциальной		значений		значений	экспоненциальной
					Наличие		модели	значений		модели	экспоненциальной
					запасов		модели	(столбец 5 –		модели		(столбец 5
№	Год				производ-		(значение	модели		от запасов		модели
					ственных	экспоненциального		от запасов		в квадрате		в квадрате
						экспоненциального				в квадрате
						тренда +сезонная		– столбец 4)		(столбец 6		в квадрате)
							компонента)	– столбец 4)		в квадрате)		в квадрате)
							компонента)			в квадрате)
1	2		3		4	5		6		7	8		9
1	2006		1		343,265	428,870		85,605		7328,228	183929,539		11,060
2			2		564,152	548,901		-15,251		232,598	301292,143		18,177
3			3		619,497	596,872		-22,625		511,903	356255,859		19,960
4			4		1 091,25	760,632		-330,616		109307,160	578560,533		35,160
5	2007		1		601,929	532,696		-69,233		4793,159	283765,407		19,394
6			2		710,923	657,343		-53,580		2870,790	432100,147		22,906
7			3		796,705	710,135		-86,570		7494,283	504292,392		25,670
8			4		833,599	878,931		45,332		2055,001	772519,913		26,858
9	2008		1		718,617	656,255		-62,362		3888,969	430671,151		23,154
10			2		763,554	786,396		22,842		521,745	618418,243		24,601
11			3		781,72	844,926		63,206		3994,951	713899,315		25,187
12			4		780,417	1019,714		239,297		57263,074	1039816,727		25,145
Итого										200 261,86	6 215 521,37		−
Ошибка: ∑(столбец 7) / ∑(столбец 8) ∙ 100 %													3,222
	СКО находим по формуле
							Е = ΣО2 / Σ(T + S)2,						(12)

где О – ошибка модели; Т – трендовое значение объема запасов; S – сезонная компонента.

Определение ошибок трендов сводится в табл. 6. Для этого сформируем таблицу и выполним расчеты:

1.В столбцы T + S внесем значения моделей, рассчитанные

ранее.

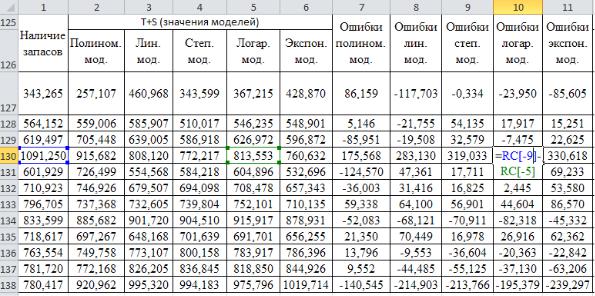
2.Значения в столбцах Ошибка модели определим как разницу между фактическим наличием запасов и значением модели (рис. 14).

3.Рассчитаем СКО для каждого периода делением каждого значения ошибки модели в квадрате на значения моделей в квадрате (рис. 15).

Рис 14. Расчет ошибок моделей

Величина полученных ошибок позволяет говорить, что построенная модель хорошо аппроксимирует фактические данные, т.е. она вполне отражает экономические тенденции, определяющие отпуск и реализацию МТР, и является предпосылкой для построения прогнозов высокого качества.

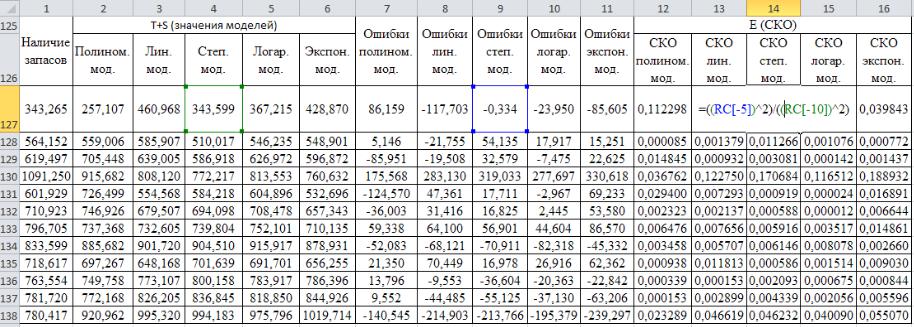
Рассчитав среднее значение СКО для каждой модели (табл. 8), определим точность моделей по формуле

точность модели = (1 – среднее значение Е) ∙ 100 %. (13)

Рис. 15. Расчет СКО для каждого периода

														Таблица 8
			Значение моделей T + S, их ошибок и среднеквадратического отклонения Е

		T + S (значение моделей)						Ошибка					E (СКО)

Наличие	Полином. модель	Линейная модель	Степ. модель	Логариф. модель	Экспон. модель	Полином. модель	.Лин модель	Степ. модель	Логар. модель	Экспон. модель	Полином. модель	.Лин модель	Степ. модель	Логар. модель	Экспон. модель
Наличие
запасов

343,265	257,107	460,968	343,599	367,215	428,870	86,159	-117,703	-0,334	-23,950	-85,605	0,112298	0,065198	0,000001	0,004254	0,039843
564,152	559,006	585,907	510,017	546,235	548,901	5,146	-21,755	54,135	17,917	15,251	0,000085	0,001379	0,011266	0,001076	0,000772
619,497	705,448	639,005	586,918	626,972	596,872	-85,951	-19,508	32,579	-7,475	22,625	0,014845	0,000932	0,003081	0,000142	0,001437
1091,250	915,682	808,120	772,217	813,553	760,632	175,568	283,130	319,033	277,697	330,618	0,036762	0,122750	0,170684	0,116512	0,188932
601,929	726,499	554,568	584,218	604,896	532,696	-124,570	47,361	17,711	-2,967	69,233	0,029400	0,007293	0,000919	0,000024	0,016891
710,923	746,926	679,507	694,098	708,478	657,343	-36,003	31,416	16,825	2,445	53,580	0,002323	0,002137	0,000588	0,000012	0,006644
796,705	737,368	732,605	739,804	752,101	710,135	59,338	64,100	56,901	44,604	86,570	0,006476	0,007656	0,005916	0,003517	0,014861
833,599	885,682	901,720	904,510	915,917	878,931	-52,083	-68,121	-70,911	-82,318	-45,332	0,003458	0,005707	0,006146	0,008078	0,002660
718,617	697,267	648,168	701,639	691,701	656,255	21,350	70,449	16,978	26,916	62,362	0,000938	0,011813	0,000586	0,001514	0,009030
763,554	749,758	773,107	800,158	783,917	786,396	13,796	-9,553	-36,604	-20,363	-22,842	0,000339	0,000153	0,002093	0,000675	0,000844
781,720	772,168	826,205	836,845	818,850	844,926	9,552	-44,485	-55,125	-37,130	-63,206	0,000153	0,002899	0,004339	0,002056	0,005596
780,417	920,962	995,320	994,183	975,796	1019,714	-140,545	-214,903	-213,766	-195,379	-239,297	0,023289	0,046619	0,046232	0,040090	0,055070
Среднее СКО											0,019197	0,022878	0,020988	0,014829	0,028548
Точность модели											98,08029	97,7122	97,9012	98,5171	97,1452

Точность модели с полиномиальным трендом равна 98,1 %, с линейным – 97,7 %, со степенным – 97,9 %, с логарифмическим – 98,5 %, с экспоненциальным – 97,1 %.

Таким образом, высокой точностью обладают все модели. Если точность колеблется в районе 97–100 %, то можно утверждать, что модель достаточно точная.

Сделаем анализ прогноза по модели с полиномиальным трендом (рис. 16). Она является достаточно точной, так как показатель ее точности один из наиболее высоких.

Производственные запасы, млн р.

1100	1091,25
	1091,25
1000
			Производственные
900		833,599	запасы
		833,599
800	796,705	781,72
800
		780,417	Полиномиальная
700		763,554	линия тренда с
700	710,923
		718,617
		718,617
600	619,497		прогнозом на
600	601,929		будущий период
	601,929		будущий период
	564,152

500
500										Полиномиальная: y = 0,0455x6 - 1,7749x5 +
										Полиномиальная: y = 0,0455x6 - 1,7749x5 +
400										+26,425x4 - 185,32x3 + 595,85x2 - 629,69x +
400	343,265										535,77,
											535,77,
											R² = 0,5874.
300											R² = 0,5874.
1	2	3	4	5	6	7	8	9	10 11 12 13 14 15 16

Квартал

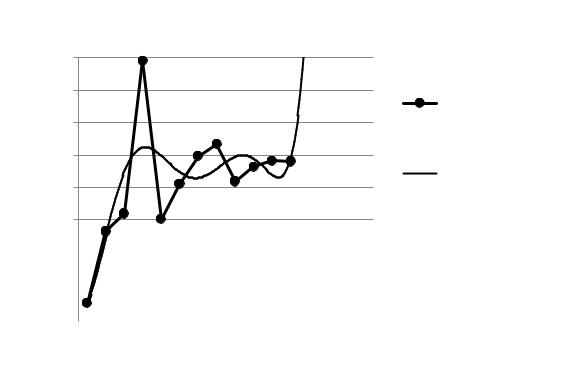
Рис. 16. Модель запасов по полиномиальной линии тренда

Проанализировав рисунок, заметим, что в начале 2006 г. наличие производственных запасов было очень мало, после чего в четвертом квартале производственные запасы резко возросли. Прогноз, сделанный на основании данных полиноминальной модели, не будет верным. Следовательно, для прогнозирования мы не можем учитывать столь нестабильный год, для более точного прогнозирования возьмем 2007 и 2008 гг. На данном этапе моделирования мы можем сделать вывод о предпочтительности модели. Выбираем модель с логарифмическим трендом. Эта модель имеет самую маленькую ошибку, которая составляет 1,5 %. Проведем новые расчеты, исклю-

чив 2006 г. и полиноминальную линию тренда. Для этого снова построим график запасов и новые линии трендов, получив новые уравнения. Рассчитаем значения линий трендов.

Алгоритм вычислений остался прежним:

1. Построение модели, описывающей наличие запасов ТМЦ (МТР) в табл. 9:

1) построим линии тренда четырех видов с помощью MS Excel: линейную, логарифмическую, степенную, экспоненциальную;

2) уравнения линий тренда принимают вид, указанный на рис. 17.

			Таблица 9
	Фактическое наличие производственных запасов

№	Год	Квартал	Наличие производственных запасов, млн р.

1		I	601,929
2	2007	II	710,923
3	2007	III	796,705
3		III	796,705
4		IV	833,599
5		I	718,617
6	2008	II	763,554
7	2008	III	781,72
7		III	781,72
8		IV	780,417

	850										Линейная линия тренда:
					833,599						y = 16,535x + 674,02,
	825				833,599						R² = 0,3216.
											R² = 0,3216.
									Экспоненциальная линия тренда:
									Экспоненциальная линия тренда:
р.	800										y = 668,92e0,024x,
р.	800										R² = 0,3401.
, млн				796,705				780,417			R² = 0,3401.
				796,705				780,417		Логарифмическая линия тренда:
	775									Логарифмическая линия тренда:
	775						781,72				y = 73,768ln(x) + 650,65,
запасы							781,72				R² = 0,5279.
						763,554					R² = 0,5279.
	750					763,554					Степенная линия тренда:
	750										Степенная линия тренда:
											y = 646,84x0,1068,
Производственные	725					718,617					R² = 0,5553.
	710,923					718,617
	710,923										Производственные
	700										Производственные
	700										запасы, млн.р.
											запасы, млн.р.
	675										Линейная линия
											тренда
	650										Экспоненциальная
											Экспоненциальная
											линия тренда
	625										Логарифмическая
		601,929									Логарифмическая
		601,929									линия тренда
	600										линия тренда
	600
	1	2	3	4	5	6	7	8			Степенная линия
								Квартал			тренда
								Квартал
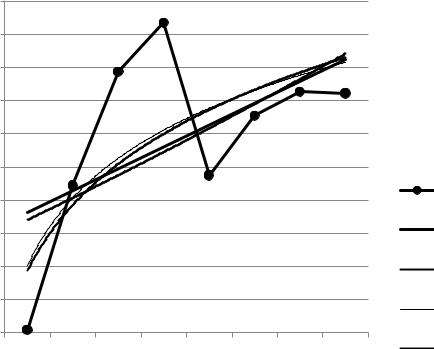
		Рис. 17. Линии трендов производственных запасов

2. Построение прогноза по уравнениям трендов (см. рисунок). В этих уравнениях х – независимая компонента (последовательность чисел от 1 до 8), а y – значения уравнения линии тренда

для каждого из х.

Используя уравнения трендов, полученные графическим способом, рассчитаем линейный, логарифмический, степенной и экспоненциальный тренды для каждого квартала (рис. 18).

Рис. 18. Расчет значений линий трендов

Рассчитаем сезонную компоненту S для каждого из уравнений тренда.

1. Из фактических данных (наличие запасов) вычитаем значения линий тренда, например логарифмического, для каждого квартала (рис. 19).

Рис. 19. Расчет данных для сезонной компоненты по значениям логарифмического тренда

2. Преобразуем полученные данные в таблицу, где в строке представлены данные для расчета сезонных компонент по кварталу, а в столбце – по году:

<<< < Предыдущая 1 23 / 53 4 5 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20221.36 Mб1m0942.pdf
#
15.11.20226.04 Mб2m0943.pdf
#
15.11.202227.62 Mб6m0944.pdf
#
15.11.20222.31 Mб3m0945.pdf
#
15.11.2022795.42 Кб1m0946.pdf
#
15.11.20222.82 Mб3m0947.pdf
#
15.11.202222.55 Mб3m0955.pdf
#
15.11.20222.77 Mб3m0960.pdf
#
15.11.2022652.7 Кб2m0962.pdf
#
15.11.2022720.8 Кб0m0963.pdf
#
15.11.2022677 Кб0m0964.pdf