
- •Основы теории высшей кинематической пары
- •Введение в теорию высшей пары, основные понятия и определения
- •Механизмы с высшими кинематическими парами и их классификация
- •Структурные схемы простейших механизмов с высшими кп
- •Достоинства механизмов с вкп
- •Недостатки механизмов с вкп
- •Угол давления в высшей паре
- •Основная теорема зацепления (теорема Виллиса)
- •Зубчатые передачи
- •Эвольвентная зубчатая передача
- •Эвольвента окружности и ее свойства
- •Параметрические уравнения эвольвенты
- •Свойства эвольвенты окружности
Эвольвентная зубчатая передача
Эвольвентная зубчатая передача - цилиндрическая зубчатая передача, профили зубьев которой выполнены по эвольвенте окружности.
Эвольвента окружности и ее свойства
Эвольвента окружности- это
плоская кривая, которая описывается
точкой прямой при ее перекатывании по
окружности, прямая при этом называется
производящей, окружность – основной
(базисной, отсюда и обозначение![]() ).
Т.е. эвольвента – это развертка окружности.
Построение эвольвенты должно обеспечивать
в любом положении равенство дуги
окружности и прямой.
).
Т.е. эвольвента – это развертка окружности.
Построение эвольвенты должно обеспечивать
в любом положении равенство дуги
окружности и прямой.
Параметрические уравнения эвольвенты

Рассмотрим схему, представленную на
рис. Так как производящая прямая
перекатывается по основной окружности
без скольжения, то дуга
![]() равна отрезку
равна отрезку![]() .
.![]() - нормаль к профилю эвольвенты, радиус
кривизны эвольвенты в данной точке.
- нормаль к профилю эвольвенты, радиус
кривизны эвольвенты в данной точке.
Профильный угол
![]() - это угол между радиус-вектором в точке
эвольвенты и касательной к эвольвенте
в этой точке, численно равен углу
давления.
- это угол между радиус-вектором в точке
эвольвенты и касательной к эвольвенте
в этой точке, численно равен углу
давления.
Уравнение эвольвенты записывается в
параметрической форме в полярных
координатах, где
![]() - эвольвентный угол,
- эвольвентный угол,![]() - радиус эвольвенты,
- радиус эвольвенты,![]() - текущая точка.
- текущая точка.
 или в общем виде
или в общем виде
из
![]() :
:
1.
![]() ,
,
2. т.к.
![]() ,
то
,
то![]() ,
откуда
,
откуда![]() - инвалюта угла, табличная величина.
- инвалюта угла, табличная величина.
Так как профильный угол и угол давления раны по величине, то окончательно получим параметрические уравнения эвольвенты:

Свойства эвольвенты окружности
Форма эвольвенты окружности определяется только радиусом основной окружности
 . При
. При эвольвента
переходит в прямую линию.
эвольвента
переходит в прямую линию.Производящая прямая является нормалью к эвольвенте в рассматриваемой произвольной точке
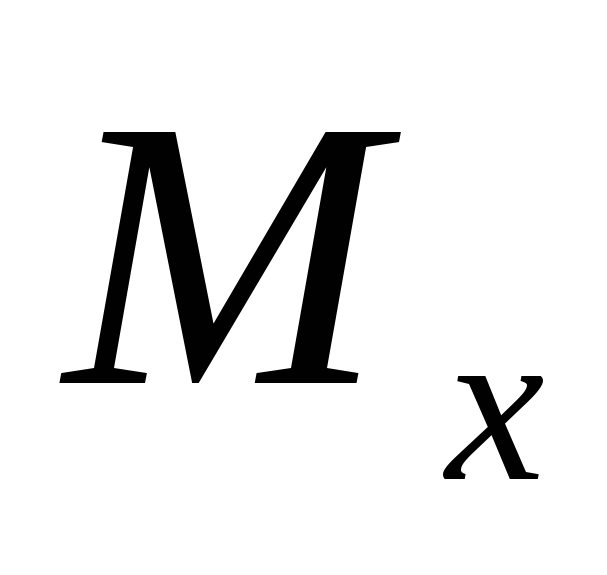 ,
при этом точка
,
при этом точка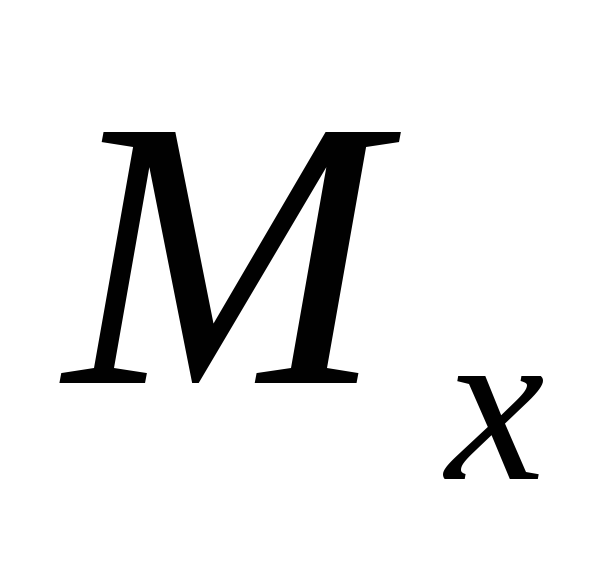 является мгновенным центром вращения
производящей прямой и, следовательно,
центром кривизны эвольвенты. Т.е. отрезок
нормали в произвольной точке эвольвенты
является мгновенным центром вращения
производящей прямой и, следовательно,
центром кривизны эвольвенты. Т.е. отрезок
нормали в произвольной точке эвольвенты равен радиусу ее кривизны и является
касательной к основной окружности.
равен радиусу ее кривизны и является
касательной к основной окружности.Эвольвента имеет две симметричные ветви и точку возврата
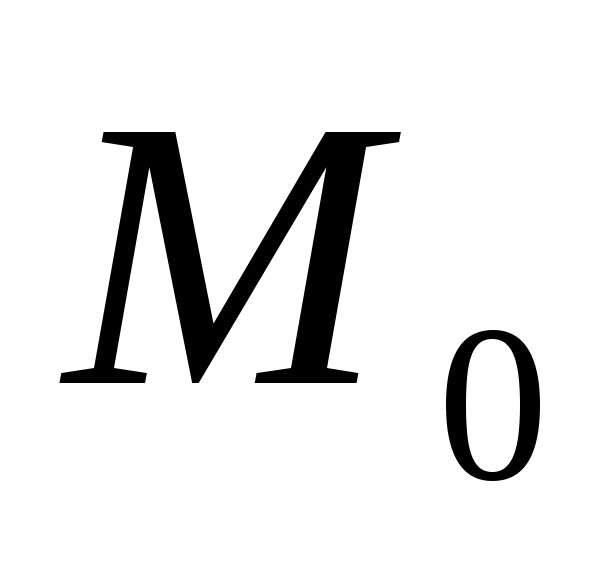 ,
лежащую на основной окружности.
,
лежащую на основной окружности.Эвольвента не имеет точек внутри основной окружности.
