
2971
.pdf
004
Р311 СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ
Реализация численных методов в различных программных средах
Методические указания для выполнения лабораторной работы
Новосибирск
2015
1
УДК [004.42+004.43]:51(076.5) Р311
Реализация численных методов в различных программ-
ных средах: Метод. указ. для выполнения лабораторной работы / Сост. Л.В. Голунова. – Новосибирск: Изд-во СГУПСа, 2015. – 11 с.
Содержат сведения о численных методах интегрирования. Показаны способы использования численных методов для решения технических задач. Дана возможность освоить численные методы для решения задач алгебры, математического анализа и дифференциальных уравнений, задач исследовательского и прикладного характера. Показано решение одной и той же задачи в различных программных средах. Приведены задания для самостоятельной работы, контрольные вопросы.
Предназначены для студентов очной формы обучения всех направлений и специальностей, изучающих дисциплину «Информатика», разделы «Моделирование», «Основы алгоритмизации и программирования».
Рассмотрены и рекомендованы к изданию на заседании кафедры «Общая информатика».
О т в е т с т в е н н ы й р е д а к т о р канд. техн. наук, доц. Д.Н. Цветков
Р е ц е н з е н т канд. физ.-мат. наук, доц. кафедры «Информационные
технологии транспорта» К.М. Шлемензон
©Сибирский государственный университет путей сообщения, 2015
©Голунова Л.В., сост., 2015
2
Введение
В методических указаниях рассмотрены наиболее употребительные численные методы интегрирования: метод прямоугольников, метод трапеций, метод парабол (Симпсона), их реализация в среде MS Excel и встроенном в пакет MS Office языке программирования VBA.
Цель работы: cформировать у студентов навыки практического использования программного обеспечения для решения прикладных задач разными способами.
Для успешного выполнения работы студент должен иметь навыки работы с операционной системой Windows, уметь разрабатывать алгоритм решения задачи и реализовывать его на языке программирования VBA, иметь навыки работы в табличном процессоре MS Excel, знать основные методы вычисления определенных интегралов.
После выполнения работы студент должен уметь использовать различное программное обеспечение для решения задач численного интегрирования.
Порядок выполнения работы:
1)познакомиться с теоретическими основами методов численного интегрирования;
2)последовательно выполнить все предложенные задания;
3)выполнить задание для самостоятельной работы;
4)представить выполненную работу преподавателю;
5)ответить на вопросы преподавателя.
3
1. Общие сведения
Под приближенным вычислением интегралов понимают приближенное вычисление значения определенного интеграла
b
f (x)dx при условии, что известны отдельные значения подын-
a
тегральной функции и некоторые ее общие свойства. Кроме того, далее будем полагать, что f (x) – кусочно-непрерывная функция.
На практике численный расчет по формулам приближенного интегрирования используют для вычисления определенных интегралов от функций, для которых не удается найти первообразные. Иногда это удобно делать и для функций, первообразные которых известны. Наиболее употребительными методами приближенного вычисления определенных интегралов является метод прямоугольников, метод трапеций и метод парабол (Симпсона).
2. Метод прямоугольников
Пусть требуется вычислить интеграл от a до b от функции f (x). Отрезок интегрирования [a; b] разбиваем точками хi = а +
+ |
b a |
i (при i = 0, 1, …, n) на n равных по длине отрезков. Тогда |
||||||||||||
n |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b |
|
|
n |
|
|
|
|
b a |
n |
|
|
|
|
|
|
f (x)dx |
|
f (c ) x |
|
|
f (c ), |
|
|||||
|
|
|
= |
lim |
lim |
|
|
(1) |
||||||
|
|
|
i |
i |
|
n |
i |
|||||||
|
|
a |
|
|
n i 1 |
|
|
|
n |
i 1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
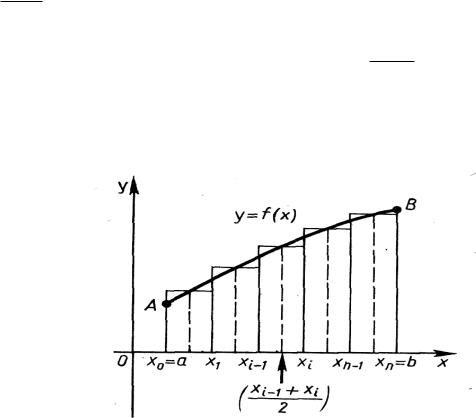
где ci [xi–1; xi] (при i = 1, …, n – некоторая точка i-го отрезка). На рис. 1 показана геометрическая интерпретация метода
прямоугольников.
Рис. 1. Геометрическая интерпретация метода прямоугольников
4
В результате преобразований формула (1) примет вид:
b
f (x)dx ≈
a
n h
i 1
f
xi
,
(2)
где h |
b a |
; x0 = a + |
h |
; хi = хi–1 |
+ h (при i = 1, 2, …, n). |
|
n |
2 |
|||||
|
|
|
|
Формула (2) называется формулой прямоугольников. При заданном значении n она обеспечивает достаточно высокую точ-
ность вычисления интеграла
b |
|
|
f (x)dx. |
a |
|
В среде программирования VBA составим программу для приближенного вычисления интегралов методом прямоугольников. Для примера рассмотрим интеграл
1 |
1 x |
3 |
|
|
|
dx. |
|||
|
||||
0 |
|
|
|
(3)
Количество шагов интегрирования (равных по длине отрез-
ков) n = 10.
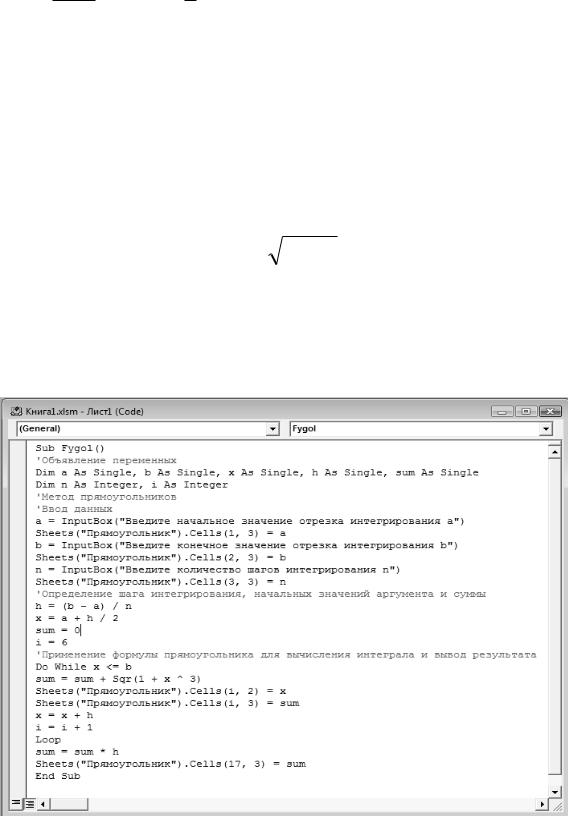
Программа вычислений по формуле (3) показана на рис. 2, результат выполнения программы на рис. 3.
Рис. 2. Программная реализация метода прямоугольников на VBA
5
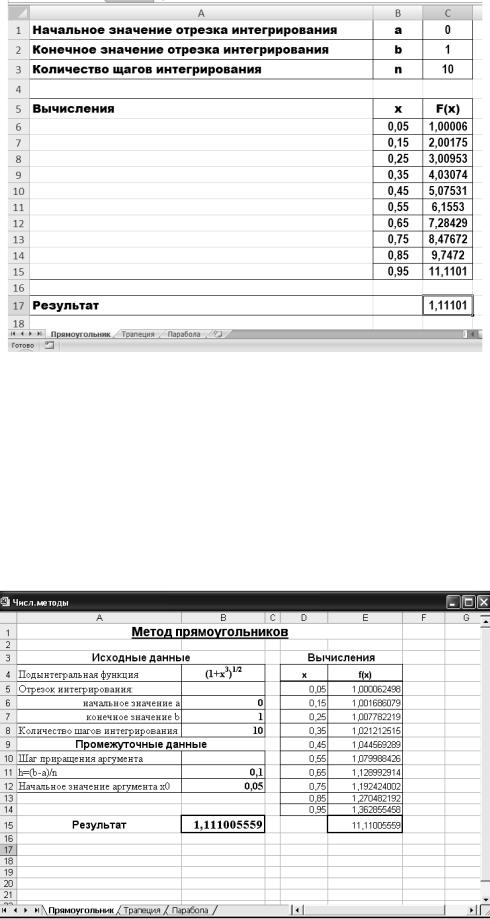
Рис. 3. Результат выполнения программы
Выполните программу при n = 20, 50, 100, 200, 1000. Проанализируйте полученные результаты.
Рассмотрим решение этого же примера в табличном процес-
соре MS Excel:
1. В ячейки B6:B8 (рис. 4) ввести исходные данные: начальное и конечное значение отрезков интегрирования, количество шагов интегрирования.
Рис. 4. Реализация метода прямоугольников в MS Excel
6
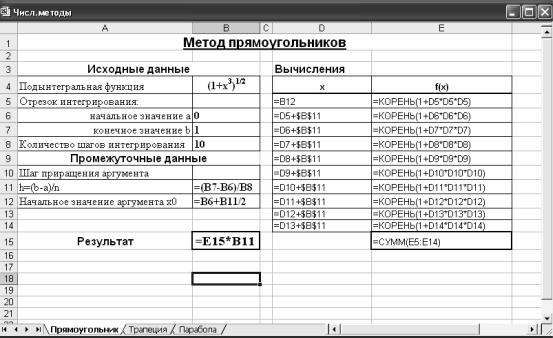
2. В ячейку B11 ввести формулу для нахождения шага приращения аргумента, соответственно в B12 – формулу начального значения аргумента (рис. 5).
Рис. 5. Реализация метода прямоугольников в MS Excel (режим формул)
3.В ячейку D5 введите значение середины первого частичного отрезка, равное начальному значению аргумента x0, в D6 – значение второго отрезка и т.д. (см. рис. 5).
4.В ячейку E5 введите формулу подынтегральной функции (см. рис. 5). Скопируйте введенную формулу в ячейки диапазона
E6:E14.
5.Выделите диапазон E5:E14. Используя кнопку ∑ строки инструментов, найдите сумму значений функции (см. рис. 4, 5).
6.В ячейке B15 вычислите конечный результат согласно формуле (2).
Результат вычислений в VBA и в электронных таблицах MS Excel оказался одинаковым.
3. Метод трапеций
Если площадь криволинейной трапеции на отрезке [xi–1; xi] за-
менить площадью трапеции (рис. 6), равной |
b a |
|
f (xi 1 ) f (xi ) |
, |
|
n |
2 |
||||
|
|
||||
то получится формула |
|
|
|
|
|
7
b
a
f (x)dx
≈
b a |
n |
f (x |
) |
|
|
i 1 |
|
|
|
|
|
n |
i 1 |
|
2 |
f
(xi )
.
(4)
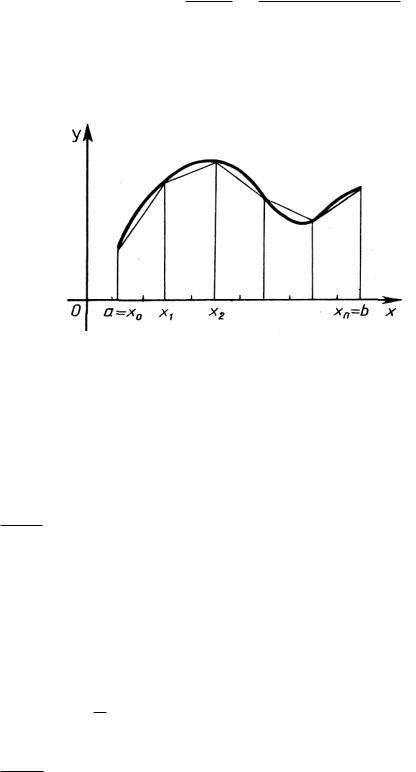
Формула (4) называется формулой трапеций для приближенного вычисления определенных интегралов. На рис. 6 показана геометрическая интерпретация метода трапеций.
Рис. 6. Геометрическая интерпретация метода трапеций
В удобном для вычислений виде записать следующим образом:
b |
f (a) f (b) |
|
f (x)dx |
≈ h |
|
a |
|
|
2 |
формулу трапеции можно
|
n 1 |
|
|
|
|
|
|
f x |
|
|
|
||
+ |
|
, |
(5) |
|||
i |
|
|||||
|
i 1 |
|
|
|
|
где
h |
b a |
; |
|
n |
|||
|
|
x0 = a; хi = хi–1 + h (при i = 1, 2, …, n).
4. Метод парабол (Симпсона)
Формула (6) называется формулой парабол (Симпсона). В удобном для практических вычислений виде формулу парабол можно записать следующим образом:
где
h
b |
|
|
|
f (x)dx |
|
a |
|
|
b a |
; x0 |
|
|
2n |
|
|
|
|
|
h |
f (a) f (b) 4 |
n |
f x |
|
|
n 1 |
f x |
|
|
|
|
|
|
2i 1 |
|
2i |
, |
|||||
|
3 |
|
|
|
|
|
|
||||
|
i 1 |
|
|
|
i 1 |
|
|
|
|
||
= a; хi = хi–1 + h (при i = 1, 2, …, 2n).
(6)
Программы вычислений по формулам (5) и (6) аналогичны приведенной выше программе для метода прямоугольников с незначительными и очевидными изменениями. Порядок выполнения расчетов в электронных таблицах также аналогичен приведенному примеру для метода прямоугольников.
8
Внести необходимые изменения в программу для вычисления определенного интеграла (3) методом трапеций и методом парабол. Также выполнить вычисления определенного интеграла (3) в табличном процессоре. Сравнить полученные результаты с итогами вычислений методом прямоугольников.
Задания для самостоятельного выполнения
Найдите приближенное значение интегралов (нечетные номера заданий – по формуле трапеций (n = 10), четные – по формуле парабол (2n = 10)):
1)составьте программу на языке программирования VBA;
2)выполните расчеты в табличном процессоре MS Excel. Задания:
1. |
1 |
|
1 x |
3 |
dx |
|
|
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 x |
4 |
|
|
|
|
|
|||||
2. |
|
|
dx |
|
|
|||||||||
|
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3. |
1 |
sin (x |
2 |
)dx |
|
|
||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4. |
2 |
|
1 0,1sin |
2 |
x dx |
|||||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
|
|
|
cos xdx |
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
sin x |
|
|
|
|
|
|
|
|
||||
6. |
3 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
x |
|
|
dx |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
dx |
|
|
|
|
|
|
|
|
|
|
7. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x ln x |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
||||||||
|
2 |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
8. |
2 |
|
|
3 cos 2x dx |
||||||||||
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 x2 dx |
|
|
|||||||||
9. |
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
dx |
|
|
|
|
|
|
|
|
|
|
10. |
|
|
|
|
|
|
|
|
||||||
1 x |
4 |
|
|
|
|
|
||||||||
|
|
0 |
|
|
|
|
|
|
|
|
||||
11. |
6 |
|
|
3 x |
2 |
dx |
|
|
|
||||||
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12. |
2 |
x cos x dx |
|
|
|
||||||||||
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13. |
2 |
cos |
5 |
x sin 2x dx |
|||||||||||
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14. |
2 |
|
|
|
|
|
|
dx |
|
|
|
|
|
||
|
2 cos (x |
2 |
|
|
|
||||||||||
|
) |
|
|
||||||||||||
|
|
|
|
||||||||||||
|
0 |
|
|
|
|||||||||||
15. |
|
|
3 |
sin x dx |
|||||||||||
|
x |
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
||
16. |
3 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
2 |
x |
dx |
|
|
|
||||
|
sin |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
||||||||
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17. |
sin 5 x dx |
|
|
|
|
||||||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
||
18. |
|
|
|
|
|
|
|
|
|
|
dx |
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
0 |
|
|
8 2x x2 |
|||||||||||
|
|
3 |
|
|
|
|
|
x |
|
|
|
|
|
|
|
19. |
|
|
|
|
|
|
|
dx |
|||||||
|
|
|
|
|
|
|
|||||||||
|
|
|
|
4 x |
2 |
|
|
|
|
||||||
|
0 |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
2
20. ctg3 x dx
4
9
Рекомендуемая литература
Основная
1. Информатика: Учеб. / Б.В. Соболь, А.Б. Галин, Ю.В. Панов, Е.В. Рашидова, Н.Н. Садовой. Ростов н/Д: Феникс, 2009. 447 с.
Дополнительная
2.Акулов О.А., Медведев Н.В. Информатика: базовый курс: Учеб. для студ. вузов. М.: Омега-Л, 2012. 576 c.
3.Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные ме-
тоды для инженеров: Учеб. пособие. М.: Высшая школа, 1994. 544 с.
4.Симонович С.В. и др. Информатика: Базовый курс / СПб.: Питер,
2013. 640 c.
5.Могилев А.В., Пак Н.И., Хеннер Е.К. Информатика: Учеб. пособие для студ. вузов / Под ред. Е.К. Хеннера. М.: Академия, 2004. 848 с.
6.Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для втузов. 14-е изд., испр. М.: ФИЗМАТЛИТ, 2004. 336 с.
7.Могилев А.В., Пак Н.И., Хеннер Е.К. Практикум по информатике:
Учеб. пособие для студ. высш. учеб. заведений / Под ред. Е.К. Хеннера.
М.: Академия, 2005. 608 с.
8.Прокопов Б.И., Попов И.А. Численные алгоритмы минимизации функций: Учеб. пособие. М.: Моск. гос. ин-т электроники и математики,
2010. 286 с.
9.Сдвижков О.А. Математика в Excel 2003. М.: СОЛОН-Пресс, 2005.
192 с.
10
