
Теория графов и её приложения
..pdfМинистерство образования и науки Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Пермский национальный исследовательский политехнический университет»
С.Ф. Тюрин
ТЕОРИЯ ГРАФОВ И ЕЁ ПРИЛОЖЕНИЯ
Утверждено Редакционно-издательским советом университета
в качестве учебного пособия
Издательство Пермского национального исследовательского
политехнического университета
2015
УДК 621.399 Т89
Рецензенты:
доктор технических наук, профессор В.А. Твердохлебов (Институт точной механики и проблем управления РАН, г. Саратов); кандидат технических наук, доцент А.И. Дерябин
(Пермский филиал высшей школы экономики)
Тюрин, С.Ф.
Т89 Теория графов и её приложения : учеб. пособие / C.Ф. Тюрин. – Пермь : Изд-во Перм. нац. исслед. политехн. ун-та, 2015. – 159 с.
ISBN 978-5-398-01501-0
Представлены основные характеристики графов и даны основные задачи, решаемые на них. Предназначено для студентов, обучающихся по специальности 090303 «Информационная безопасность автоматизированных систем», 090104 «Комплексное обеспечение информационной безопасности автоматизированных систем», изучающих дисциплину «Теория графов и её приложения», для магистров, изучающих дисциплину «Исследование операций», а также студентам, изучающим дисциплину «Дискретная математика», «Математическая логика и теория алгоритмов».
Будет полезно аспирантам для проведения научных исследований и преподавателям.
УДК 621.399
ISBN 978-5-398-01501-0 |
© ПНИПУ, 2015 |
2
ОГЛАВЛЕНИЕ |
|
Введение ……………………………………………………………. .. |
5 |
1. Основные характеристики графов ................................................. |
9 |
1.1. Хроматическое число графа ............................................... |
9 |
1.2. Теорема Кёнига .................................................................... |
12 |
1.3. Планарность графов ............................................................. |
12 |
1.4. Теорема Понтрягина – Куратовского ................................. |
14 |
1.5. Гамильтонов граф ................................................................ |
16 |
1.5.1. Необходимое условие существования |
|
гамильтонова цикла в графе................................................ |
18 |
1.5.2. Задача коммивояжёра ................................................ |
19 |
1.6. Метрические характеристики графов ................................ |
20 |
1.6.1. Диаметр и радиус графа ............................................ |
20 |
1.6.2. Плотность графа ........................................................ |
22 |
1.6.3. Покрытия, независимость, связность ....................... |
23 |
1.6.4. Нахождение множества внутренней устойчивости |
|
орграфа ................................................................................. |
26 |
1.6.5. Нахождение множества внешней устойчивости |
|
орграфа ................................................................................. |
27 |
1.6.6. Число вершинной связности ..................................... |
28 |
1.6.7. Пример исследования графа ..................................... |
29 |
2. Решение экстремальных задач на графах ..................................... |
37 |
2.1. Нахождение кратчайшего пути в графе с рёбрами |
|
единичной длины ........................................................................ |
38 |
2.2. Нахождение кратчайшего пути в графе с рёбрами |
|
не единичной длины ................................................................... |
41 |
2.3. Нахождение максимального потока в транспортной сети |
|
(flow network) .............................................................................. |
43 |
2.5. Решение транспортной задачи ............................................ |
49 |
2.5.1. Решение транспортной задачи по критерию |
|
стоимости ............................................................................. |
51 |
2.5.2. Решение транспортной задачи по критерию |
|
времени ................................................................................. |
56 |
3. Перечисление деревьев. Код Прюфера ......................................... |
61 |
|
3 |
4. |
Граф Марковской цепи ................................................................... |
67 |
5. |
«Жизненные» приложения теории графов: теорема о свадьбах |
|
и головоломка о вечеринке................................................................. |
71 |
|
|
5.1. Трансверсаль ........................................................................ |
71 |
|
5.2. Теорема Холла (или теорема о свадьбах) ........................... |
72 |
|
5.3. Головоломка о вечеринке .................................................... |
73 |
6. |
Сеть Петри ....................................................................................... |
76 |
|
6.1. Пример сети Петри .............................................................. |
77 |
|
6.2. Моделирование сетей Петри с использованием |
|
|
свободно распространяемого программного продукта |
|
|
GRaph INterface ........................................................................... |
82 |
7. |
Графическое представление схемы алгоритма. Реализация |
|
схемы алгоритма конечным автоматом ............................................ |
87 |
|
8. |
Приложения теории графов в теории групп.................................. |
92 |
|
8.1. Группа S3 ............................................................................... |
92 |
|
8.2. Группа S4 ............................................................................... |
99 |
|
8.3. Автоморфизмы графов ........................................................ |
101 |
Заключение .......................................................................................... |
108 |
|
Список литературы ............................................................................. |
111 |
|
Приложения ......................................................................................... |
114 |
|
4

ВВЕДЕНИЕ
Считается, что теория графов ведёт свою историю с задачи Леонарда Эйлера о кенигсбергских мостах (1736 г.) [1–5].
Граф, соответствующий расположению островов (1, 4), берегов (2, 3), мостов (рёбра a, b, c, d, e, f, g – мосты), представлен на рис. В1.
Задача заключается в прохождении по всем мостам (рёбрам графа) и возвращении в исходную точку (вершину графа).
Эйлерова цепь в графе – это маршрут, проходящий по всем ребрам графа и притом только по одному разу. Эйлеров цикл – это эйлеров путь, являющийся циклом. Эйлеров граф – граф, содержащий эйлеров цикл.
а
Рис. В1. Задача о кенигсбергских мостах: а – семь мостов через реку Преголь, на которой два острова; б – соответствующий граф
Эйлер показал, что конечный неориентированный граф G имеет такой цикл тогда и только тогда, когда он связан и степени всех его вершин четны.
В графе, соответствующем задаче о кенигсбергских мостах, все вершины нечетны. Следовательно, эта задача на рис. В1 неразрешима.
5

Статья Эйлера, посвящённая этой задаче, написана на латинском языке в период его работы в Российской академии наук и использует «геометрическую» терминологию (рис. В2) [6].
Рис. В2. Оригинальная статья Эйлера на латинском языке и с «геометрической» терминологией
По существу, задача Эйлера – задача нахождения эйлерова цикла – это задача оптимизации, минимизации, например, при обеспечении безопасности, «охране» или «мониторинге» мостов – рёбер графов или других объектов – линий связи, дорог, трубопроводов, коридоров объекта сложной архитектуры и пр. Но она не всегда имеет решение в соответствии с условием Эйлера.
На данный момент в Калининграде, как ни странно, семь мостов, и граф, построенный на основе островов и мостов Калининграда, по-прежнему не имеет эйлерова цикла [5].
Дальнейшее развитие теория графов получила в ХIХ веке в связи с зарождением электротехники (законы Г. Кирхгофа) [7].
6

Г. Кирхгоф |
Фрэнк Харари (Frank Harary) |
(1824–1887) |
(1921–2005) |
Теория графов стала активно применяться с 30-х годов ХХ века в связи с развитием вычислительной техники, информатики, программирования, кибернетики, дискретной математики, исследования
операций и др. |
|
|
|
|
Признанным |
основателем |
совре- |
|
|
менной теории графов является Фрэнк |
|
|||
Харари – американский математик, спе- |
|
|||
циализировавшийся в теории графов [8]. |
|
|||
Фрэнк Харари |
написал известную |
|
||
книгу «Теория графов» (1969) (рис. В3). |
|
|||
В СССР, за рубежом, на постсовет- |
|
|||
ском пространстве был широко известен |
|
|||
Александр Александрович Зыков [9] – |
|
|||
советский и украинский математик, одна |
|
|||
из ключевых фигур в создании теории |
|
|||
графов. |
|
|
Рис. В3. Обложка книги |
|
В 1964 году в Новосибирске он за- |
||||
Ф. Харари «Теория графов» |
||||
щитил докторскую |
диссертацию. |
В те |
|
|
годы в СССР теория графов была явлением новым и вызывала иногда неприятие у математиков классического направления. Многим из
7

них казалось, что теория еще не достигла такого уровня, на котором возможны докторские диссертации. Поэтому Высшей аттестационной комиссией (ВАК СССР) была назначена его повторная защита – «перезащита» докторской диссертации в математическом институте им. В.А. Стеклова, которая прошла успешно, и А.А. Зыков получил учёную степень доктора физико-математических наук.
Александр Александрович Зыков (1922–2013)
Учитывая педагогический опыт Зыкова, ему сразу присвоили и учёное звание профессора.
Во время работы в Новосибирске он создал первый в Советском Союзе семинар по теории графов.
В1969 году Зыков издает классический труд «Теория конечных графов».
Внастоящее время теория графов является широко используемым математическим аппаратом, в том числе в информатике, в информационных технологиях и системах, в маршрутизации (Routing) – процессе определения маршрута следования информации в сетях связи, в новой науке компьютерной химии и пр.
Теория графов содержит большое количество нерешённых проблем и пока не доказанных гипотез.
8
1. ОСНОВНЫЕ ХАРАКТЕРИСТИКИ ГРАФОВ
Первую книгу конкретно по теории графов «Теория конечных и бесконечных графов» опубликовал в 1936 году венгерский математик Денеш Кёниг [10].
Он увлёкся графами, находясь под впечатлением известной задачи о раскраске любой географической карты всего четырьмя красками. Считается, что впервые её сформулировал студент Де Моргана Ф. Гутри [11] в 1852 году.
1.1. Хроматическое число графа |
|
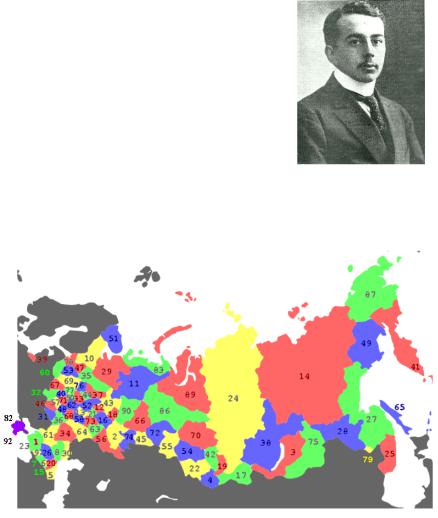
Административная карта России, рас- |
Денеш Кёниг (1884–1944) |
крашенная в четыре цвета, изображена на |
венгерский математик |
рис. 1.1. |
|
|
|
|
|
Рис. 1.1. Административная карта России, раскрашенная в четыре цвета (с Крымом и Севастополем!)
9

Для простых карт достаточно и трёх цветов, а четвёртый цвет начинает требоваться, например, тогда, когда имеется одна область, окруженная нечетным числом других, которые соприкасаются друг с другом, образуя цикл.
Хроматическое число графа G – минимальное число цветов, в которые можно раскрасить вершины графа G так, чтобы концы любого ребра имели разные цвета [11]. В теории графов теорема четы-
рёх красок формулируется так: хроматическое число плоского графа не превосходит 4. Кроме вершинной рассматривается также и рёберная раскраска графов.
Хроматическое число используется, например, в сотовой связи. Основной идеей, на которой базируется принцип сотовой связи, является повторное использование частот в несмежных сотах. Группа сот c различными наборами частот называется кластером (рис. 1.2, 1.3).
Рис. 1.2. Повторное использование частот в несмежных сотах: D – «защитный интервал»; R – радиус ячейки
10
