Теория графов и её приложения

8.3. Автоморфизмы графов

ТЕОРЕМА Фрухта Р. (1938 г.) Каждая конечная группа изоморфна группе автоморфизмов некоторого графа.

Ранее мы встречались с понятием изоморфизма (своего рода эквивалентности) графов.

Изоморфизм́ (от др.-греч. ἴσος – «равный, одинаковый, подобный» и µορφή – «форма») .

Автоморфизм Aut(G) графа G есть отображение множества вершин на себя, сохраняющее смежность.

Множество таких автоморфизмов образует вершинную группу графа или просто группу графа.

Группа подстановок на множестве ребер называется реберной группой графа.

Таким образом, автоморфизм графа – это его изоморфизм на себя. У любого графа существует тривиальный автоморфизм – тожде-

ственный.

Иногда группу автоморфизмов графа легко найти именно из чисто геометрических соображений при удачном изображении графа. Автоморфизм есть не что иное, как преобразование графа (геометрической фигуры), при котором граф совмещается с самим собой. Поэтому группу автоморфизмов графа можно изучать, анализируя его как геометрическую фигуру.

Исследование автоморфизмов графов используется в теории представлений групп. Смысл использования представлений групп заключается в том, что задачи из теории групп сводятся к более наглядным задачам – в нашем случае из теории графов.

Рассмотрим примеры автомофизмов (для вершинных групп графа). Используем свободно распространяемый программный про-

дукт GRIN [20].

В качестве одной из опций там имеется опция Automorphism (Группа автоморфизмов): определяются и выводятся в окно результатов все перестановки, которые являются автоморфизмами графа. Процедуры отличаются лишь способом порождения перестановок,

101

и в первом случае перестановки будут выводиться в лексикографическом порядке.

Например, если в окне результатов появляется строка (3,2,1,4,6,5), это означает, что автоморфизмом графа является подстановка следующего вида:

1,2,3,4,5,6

3,2,1,4,6,5

Очевидно, что граф, состоящий из одной вершины, имеет тождественный автоморфизм.

Граф, состоящий из двух вершин и одного ребра, имеет две перестановки (рис. 8.8).

Следовательно, первая перестановка – тождественная, вторая – вместо вершины 1 подставляется вершина 2 и вместо вершины 2 подставляется вершина 1. Таким образом, получаем поворот графа

(рис. 8.9).

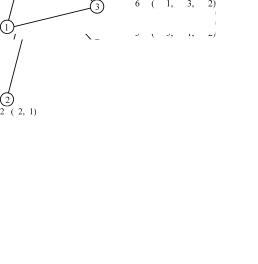
Граф, состоящий из трёх вершин и трёх ребер, имеет шесть перестановок (рис. 8.10).

Рис. 8.10. Автоморфизмы графа, состоящего из трёх вершин и трёх ребер

102

Это мы уже рассматривали выше! Граф «крутится» вокруг осей симметрии.

Следующий граф можно «крутнуть» только один раз, поменяв вершины 1, 2 местами (рис. 8.11).

Рис. 8.11. Автоморфизм (2,1,3,4) графа из четырех вершин

Аналогично всё и для графа, изображенного на рис. 8.12.

Рис. 8.12. Автоморфизм (2,1,3,4,5) графа из пяти вершин («Крутится» также только ребро 1,2)

Если введём ещё две вершины и два ребра к вершине 4, то получим следующее (рис. 8.13).

Рис. 8.13. Автоморфизмы графа из семи вершин

103

Следовательно, меняются местами вершины (6, 7); (1, 2); (и 1, 2

и 6, 7).

Граф на рис. 8.14 имеет только одну подстановку (кроме тождественной), поскольку теперь вершина 6 связана с вершиной 2, а вершина 7 – с вершиной 1:

Рис. 8.14. Автоморфизм графа из семи вершин и десяти ребер

Граф – цикл из четырех вершин и имеет восемь подстановок (считая тождественную) (рис. 8.15).

Рис. 8.15. Автоморфизм циклического графа из четырех вершин

Зато у полного графа из четырех вершин есть двадцать четыре подстановки (рис. 8.16).

104

Рис. 8.16. Автоморфизм полного графа из четырех вершин

Если убрать ребра 2,3, то получим всего три подстановки

(рис. 8.17).

Рис. 8.17. Автоморфизмы неполного графа из четырех вершин

Сначала 3 и 2 меняются местами, потом 1 и 4, потом (3 и 2)

и (1 и 4).

Иногда автоморфизм легче «уловить» для дополнения графа до полного (рис. 8.18).

105

Рис. 8.18. Дополнение до полного графа на рис. 8.17

Можно доказать, что графы изоморфны тогда и только тогда, когда изоморфны их дополнения. Это используется при доказательстве изоморфизма графов.

Рассмотрим граф – некоторое дерево (рис. 8.19) – оно легко «крутится».

Рис. 8.19. Автоморфизмы некоторого дерева

Для «треугольника», вложенного в «треугольник», получаем двенадцать подстановок (рис. 8.20).

Рис. 8.20. Автоморфизмы «треугольника», вложенного в «треугольник»

106

В случае ориентированного графа число подстановок уменьша-

ется (рис. 8.21).

Рис. 8.21. Автоморфизмы ориентированного графа из трех вершин

Наконец, для некоторого ориентированного «треугольника», вложенного в «треугольник», имеем только две подстановки

(рис. 8.22).

Рис. 8.22. Автоморфизмы некоторого ориентированного «треугольника», вложенного в «треугольник»

107

ЗАКЛЮЧЕНИЕ

Теория графов – ещё относительно молодая наука с не полностью сформировавшимся понятийным аппаратом и терминологией. Даже в программном продукте GRaph INterface (GRIN) один и тот же объект может называться то графом, то сетью, хотя сеть – это разновидность графов, т.е. менее широкое понятие, чем граф. Вершины сети иногда называют узлами.

Мы уже знакомились с теорией Рамсея (1928 г. – «Головоломка о вечеринке»), который доказал, что полная неупорядоченность невозможна. Каждое достаточно большое множество некоторых объектов обязательно содержит высокоупорядоченную структуру.

Цифровое тысячелетие – «Digital millennium», новые информационные технологии, WWW – глобальная сеть – мировая «паутина» сообщают теории графов новый мощный импульс развития.

Так, в последнее время стал выделяется так называемый граф «Мир тéсен» (маленький мир – Small World – такое название есть и в закладках GRaph INterface (GRIN) – разновидность графа, который имеет следующее свойство: если взять две произвольные вершины, то они с большой вероятностью не являются смежными, однако одна достижима из другой посредством небольшого количества переходов через другие вершины.

Граф «Мир тесен» определяется как сеть, в которой типичное расстояние между двумя произвольно выбранными вершинами (количество шагов, необходимых, чтобы достичь одну из другой) растёт пропорционально логарифму от числа вершин сети.

Много реально существующих графов хорошо моделируются графом «Мир тесен». Социальные сети, нейронные сети, связность Интернета, вики-сайты, такие как Википедия, карты дорог (но не в России!), пищевые цепочки и другое, проявляют свойства графа «Мир тесен».

В социальной сети проявляется такой эффект: незнакомых людей связывает небольшое количество промежуточных знакомых. Опять знакомых!

108

Такие графы иногда называют «стохастическими» или «вероятностными», и они могут быть классифицированы в соответствии с двумя показателями: коэффициентом кластеризации и средним расстоянием от одной вершины до другой (также известным как длина кратчайшего пути в среднем).

Коэффициент кластеризации – это мера степени, в которой вершины графа имеют тенденцию объединяться.

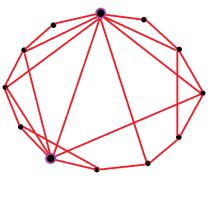
На рис. З.1 представлен пример графа «Мир тесен».

З.1. Пример графа «Мир тесен»

Впримере графа «Мир тесен» выделены вершины – хабы с высокими степенями. Средняя степень вершины = 1,917. Средняя длина кратчайшего пути = 1,803. Коэффициент кластеризации = 0,522.

Высокий коэффициент кластеризации свидетельствует о тенденции графа содержать в себе полные подграфы – клики или «почти» клики.

Граф «Мир тесен» был использован для оценки показателя возможности использования информации, хранящейся в больших базах данных (Small World Data Transformation Measure). Чем больше связи базы данных похожи на граф «Мир тесен», тем более вероятно, что пользователь будет в состоянии извлечь информацию в будущем.

Впрограмме GRaph INterface (GRIN) характеристики графа Small World используются для социологических целей. Граф «Мир

109

тесен» обладает своего рода надёжностью – связность сохраняется при повреждениях или, точнее, дефектах (отказах).

В биологических системах это может отражать как бы эволюционное преимущество такой «топологии». В технических системах может быть применим подход профессора Каравая Михаила Фёдоровича (Институт проблем управления РАН России).

Сеть строится с учётом парирования заданного количества отказов (сохранения связности), причём для синтеза отказоустойчивой по заданным характеристикам сети применяется комбинаторный подход, известный нам по курсу дискретной математики – так называемые комбинаторные конфигурации общего вида – блок схемы

(block design).

Таким образом, теория графов активно развивается и ждёт новых исследователей!

110