2.3. Определение передаточных функций.

Операторная схема замещения для четырехполюсника при нулевых начальных условиях:

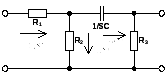
Рисунок 14. Операторная схема замещения четырехполюсника

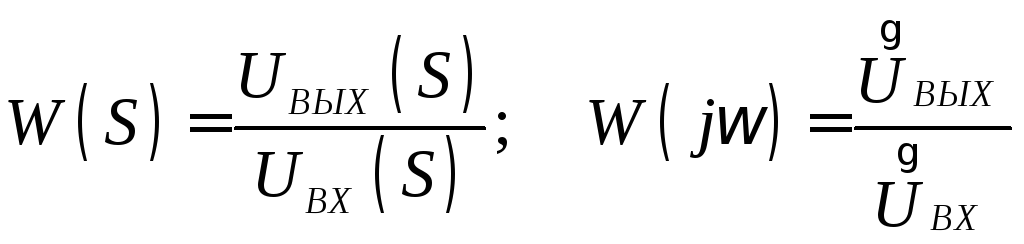
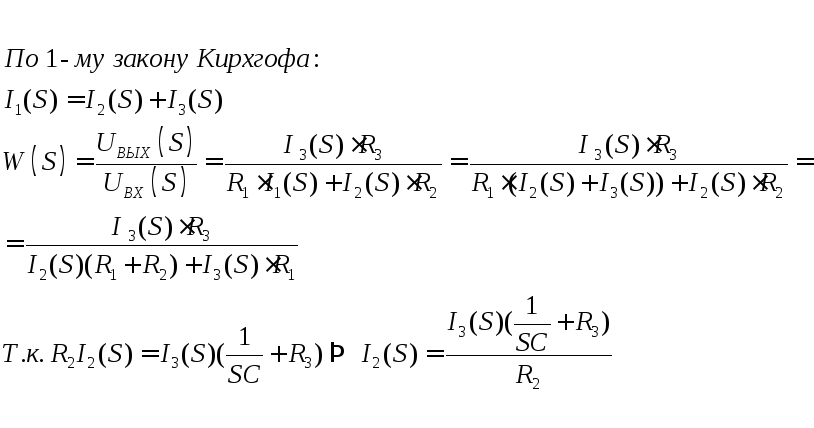
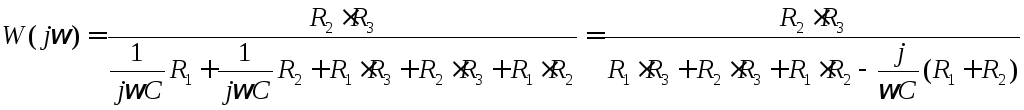
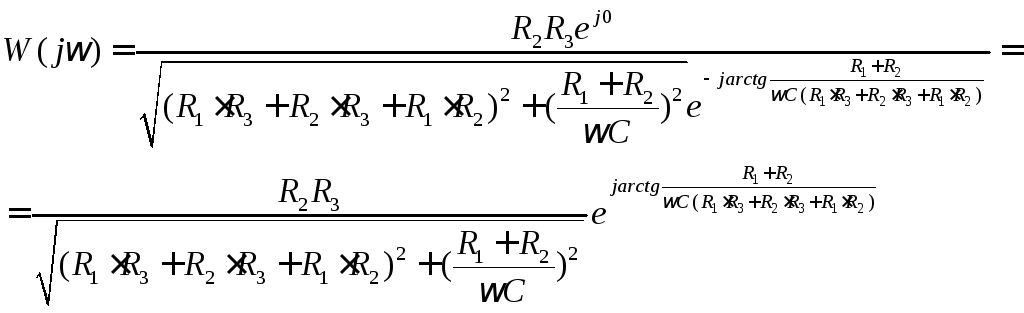
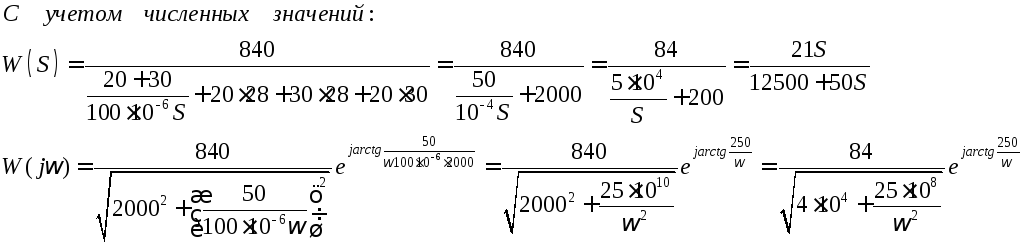
Следовательно, 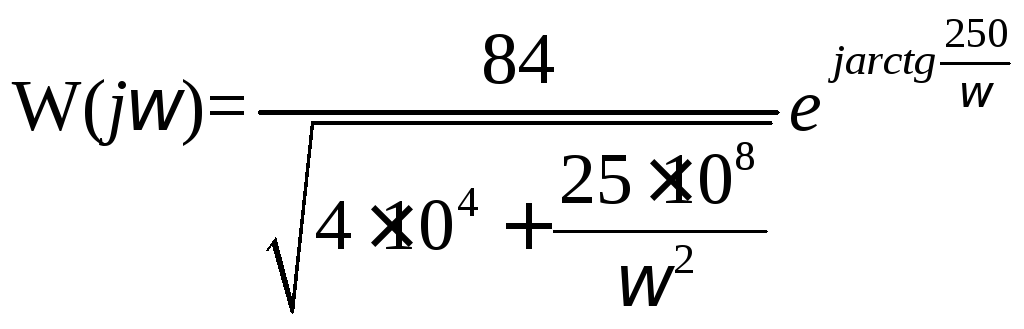- передаточная функция.

2.4. Определение амплитудно- и фазочастотных характеристик, uВых при заданном uВх.

Из пункта 2.3 следует, что:

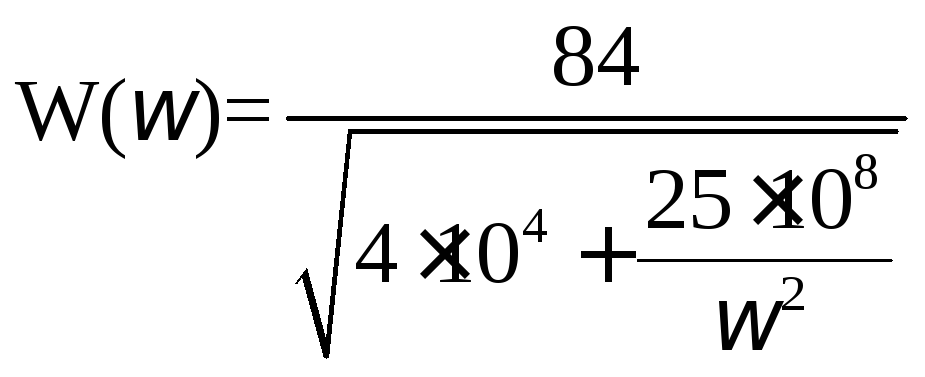- амплитудочастотная характеристика;

- фазочастотная характеристика

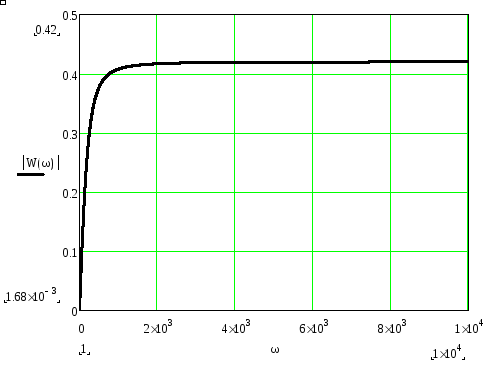
Рисунок 15. АЧХ четырехполюсника

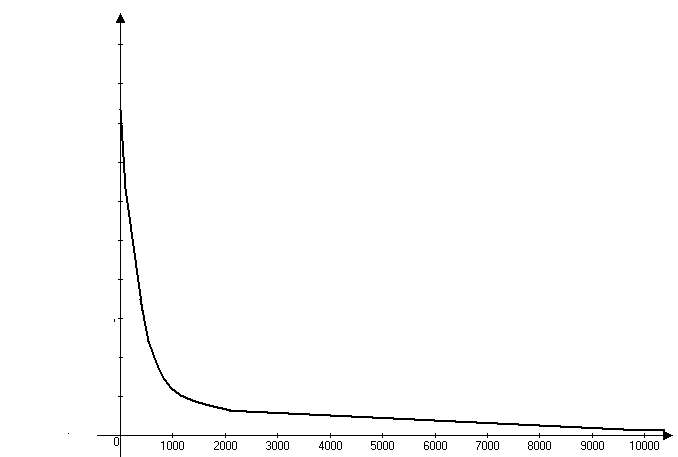
Рисунок 15. ФЧХ четырехполюсника

2.5. Определить, какое реактивное сопротивление нужно подключить к схеме, чтобы u_ВХ и i_ВХ совпадали по фазе (резонанс тока или напряжения). Определить входное сопротивление(проводимость), входной ток и добротность колебательного контура.

Т.к. в схеме из реактивных элементов присутствует только конденсатор, то подключаемый реактивный элемент должен оказаться катушкой с комплексным сопротивлением .

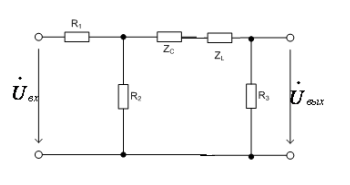
Рисунок 16. Подключение нагрузки к выходным клеммам

Условие резонанса напряжений: Z_вх=a+jb, b=0

Найдем :

Т.к. ,ивключены последовательно то:

Т.о. резонанс напряжения будет тогда, когда

Т.к.

Значит

Найдем индуктивность подключаемой катушки:

Найдем входное сопротивление при резонансе напряжений:

Определим входной ток колебательного контура:

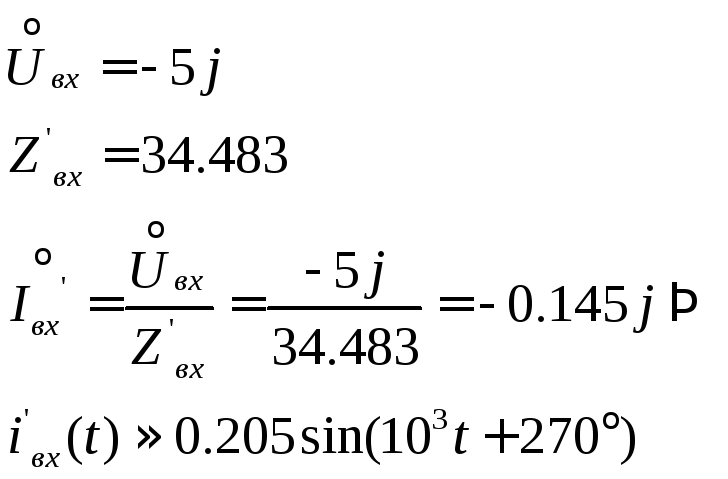
Отношение действующих значений входных токов в отсутствие резонанса и при его наличии:

Определим добротность колебательного контура:

, где b – реактивное сопротивление подключаемой катушки;

g – активное сопротивление цепи.

Т.е.

2.6. Определение амплитудно- и фазочастотных характеристик схемы в режиме резонанса.

Если в схеме резонанс напряжений, то входное сопротивление может быть выражено по формуле:

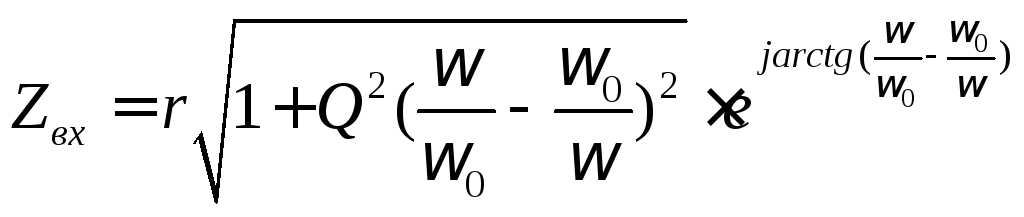, где

r– входное сопротивление при резонансной частоте;

Q– добротность контура;

- резонансная частота.

Определим характеристики контура:

• АЧХ:

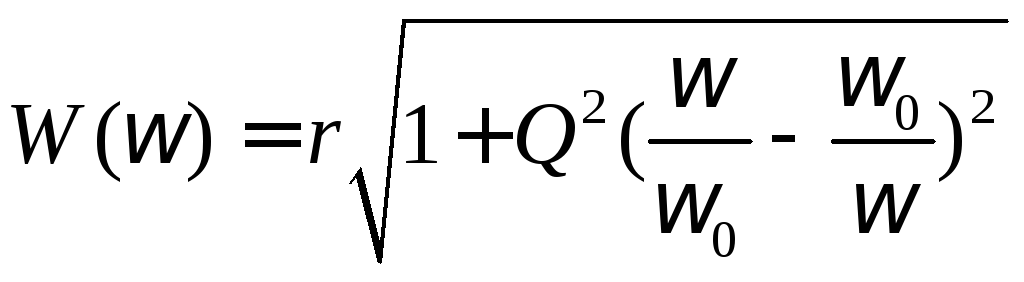
Т.к. , то

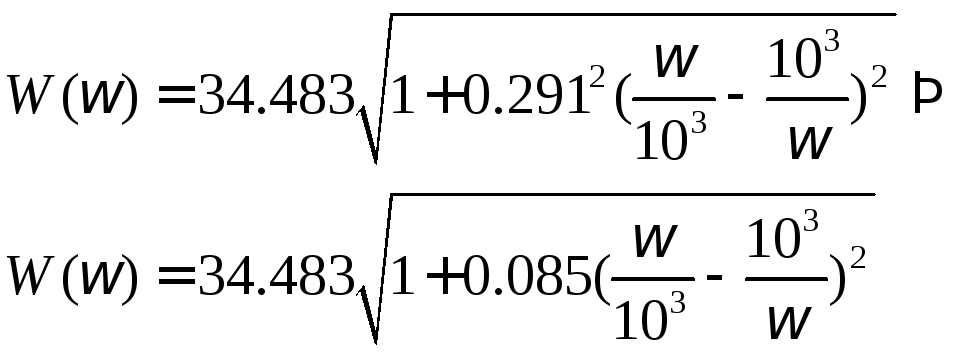
• ФЧХ:

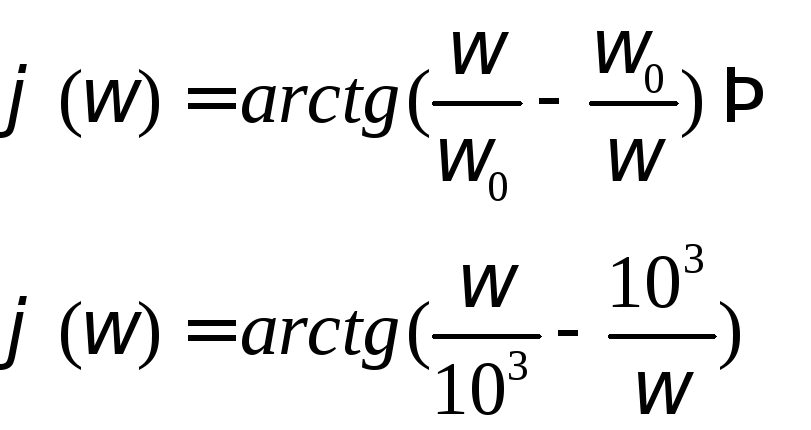
Рассчитаем значение АЧХ и ФЧХ схемы в режиме резонанса для некоторых значений :

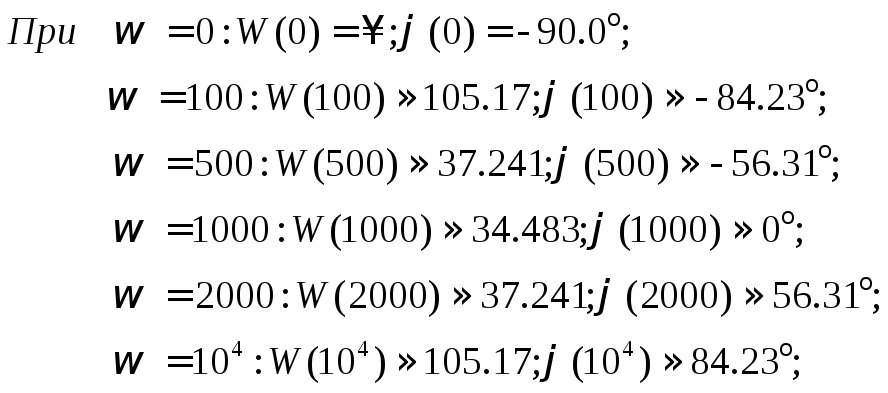
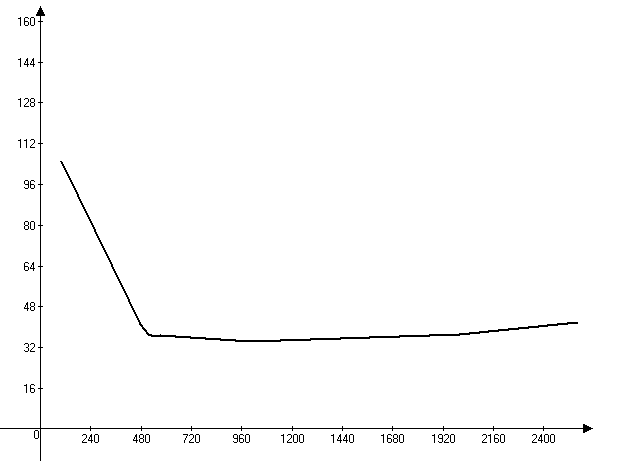
Рисунок 17. АЧХ четырехполюсника при резонансе

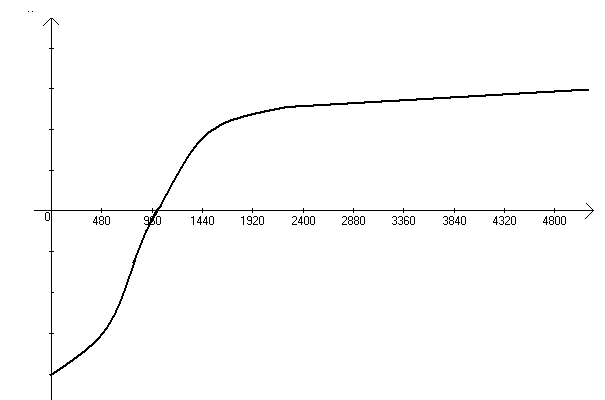
Рисунок 18. АЧХ четырехполюсника при резонансе

2.7. Построение годографа передаточной функции.

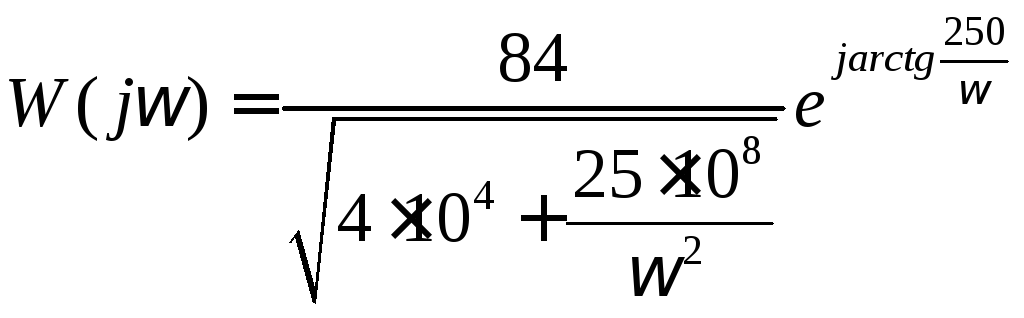
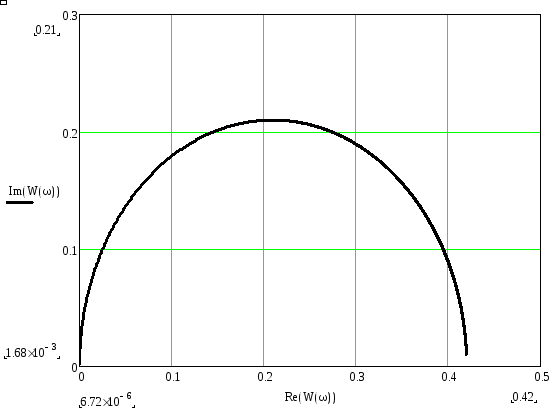
Рисунок 19. Годограф передаточной функции

3. Расчет установившихся значений напряжений и токов в электрических цепях при несинусоидальном воздействии

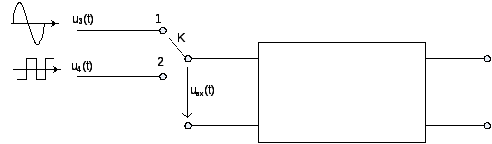
Рисунок 20. Общая схема четырехполюсника

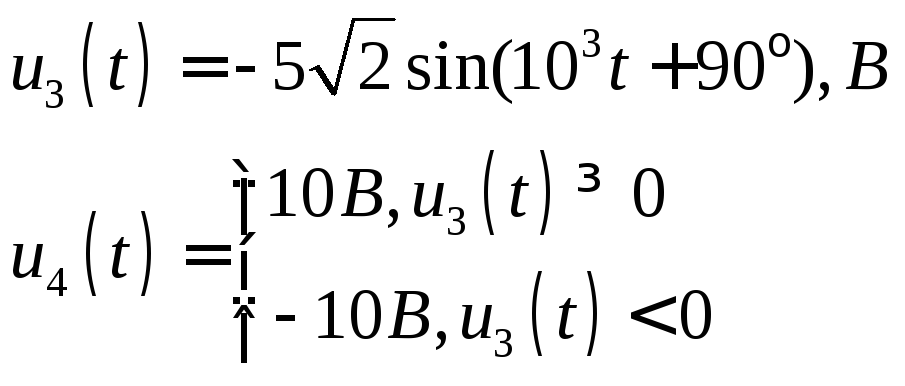
Переключатель К переводится в положение 2 в момент времени, когда т.е. когда начинается положительный импульс напряжения. Это происходит при условии

По условию, для , а для

3.1. Расчет i_ВХ(t) и u_ВЫХ(t) частотным методом c представлением входного напряжения u₄(t) в виде ряда Фурье.

Представим в виде ряда Фурье до 5-й гармоники:

,

где k = 1, 3, 5; , = 10 В.

Тогда для входного напряжения:

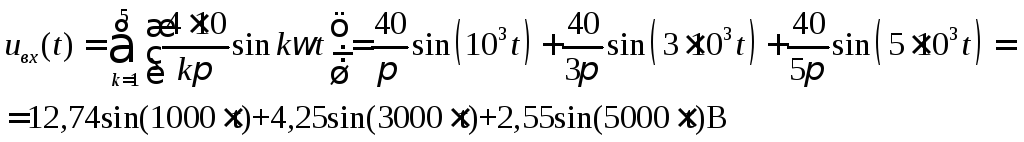
Определим выходное напряжение:

,

где и -АЧХ и ФЧХ соответственно

Из 2.4 известно, что .

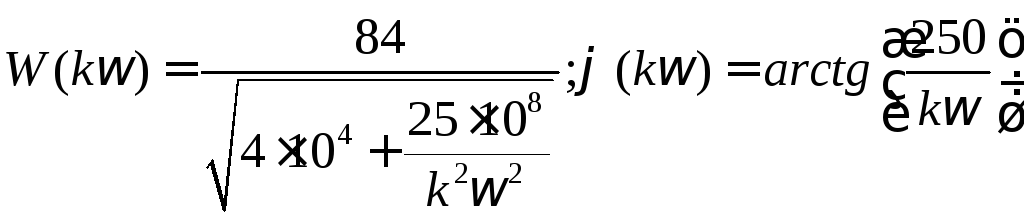Тогда:

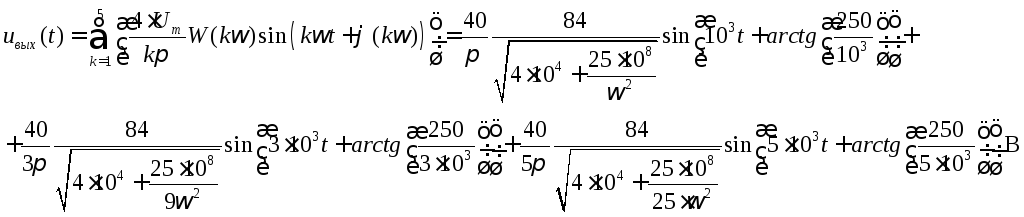
Получили:

Закон изменения тока i_вх(t):

Запишем входное сопротивление в зависимости от гармоники:

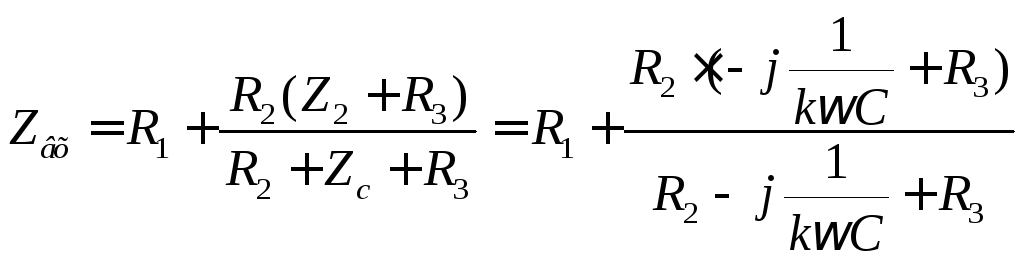
Расчет для 1-й, 3-й, 5-ой гармоник входного тока:

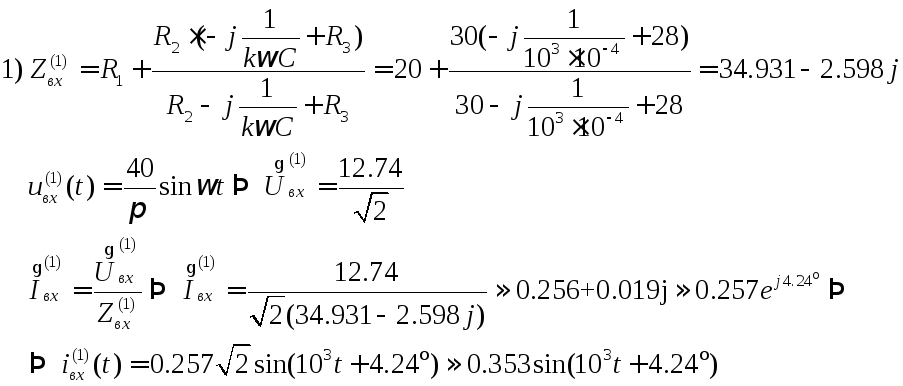
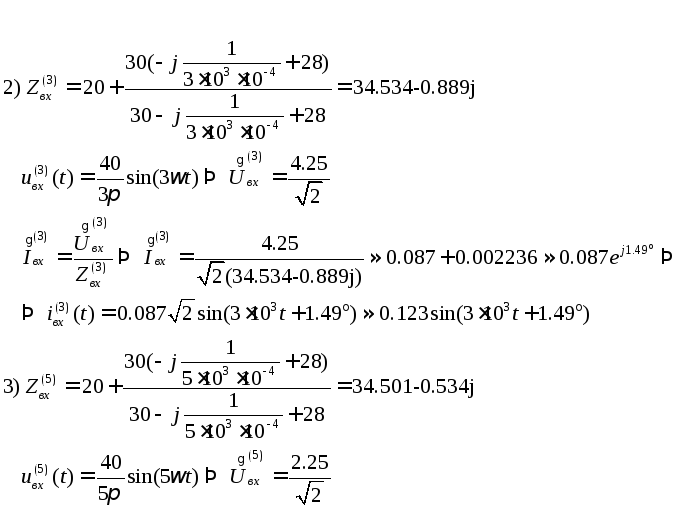
Получили, что мгновенное значение входного тока:

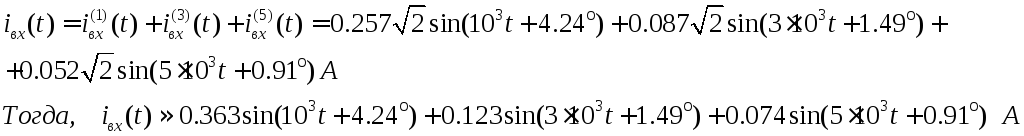
3.2. Построение графиков напряжения и тока

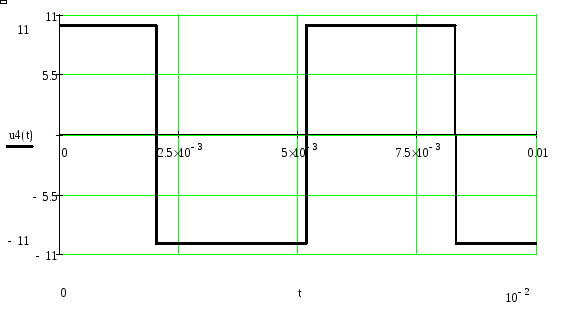
Рисунок 21. График входного напряжения

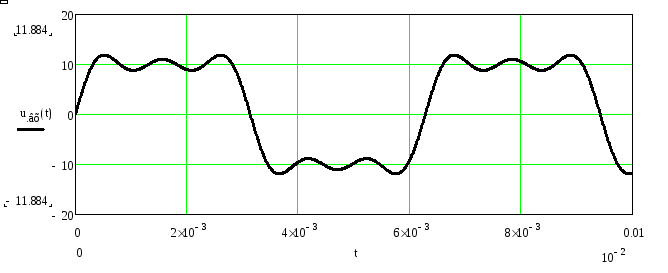
Рисунок 22. График входного напряжения, разложенного в ряд Фурье до 5-й гармоники

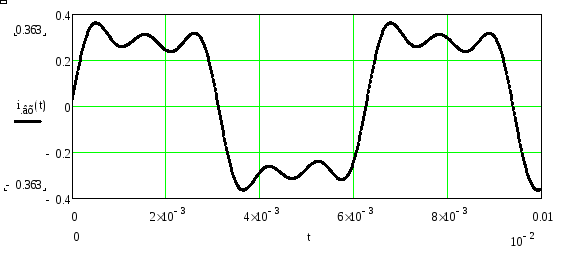
Рисунок 23. График входного тока, рассчитанного частотным методом

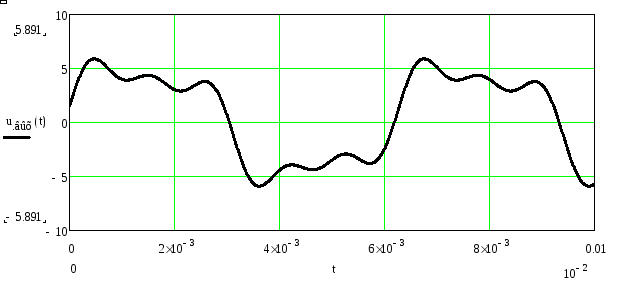
Рисунок 24. График выходного напряжения, рассчитанного частотным методом

3.3 Определение действующих значений несинусоидальных токов и напряжений из расчетов п.3.1, а также активную мощность, потребляемую четырехполюсником, коэффициенты искажения ,.

Найдем действующие значения несинусоидальных токов и напряжений п.3.1:

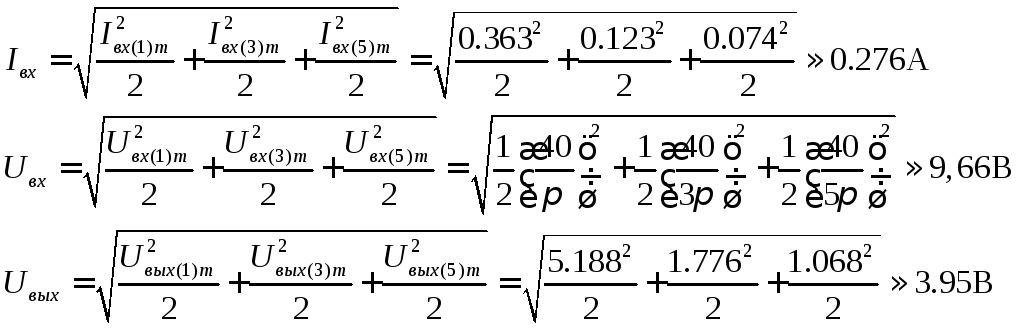
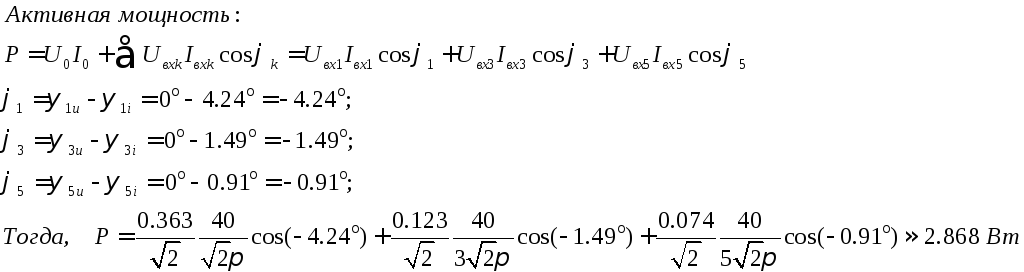
Определим значения коэффициентов искажения ,:

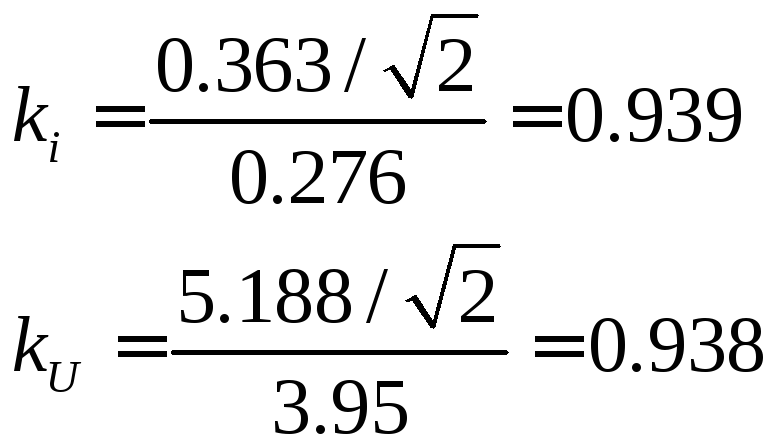
4. Расчет переходных процессов классическим методом

4.1. Переходная и импульсная характеристики для входного тока и выходного напряжения.

а) Определим переходную и импульсную

характеристики классическим методом.

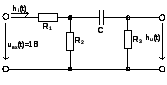
Рисунок 25. Схема четырехполюсника

Характеристическое уравнение:

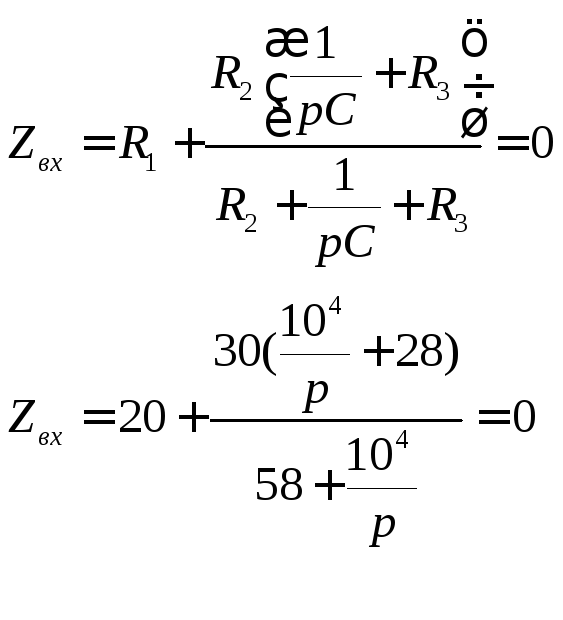
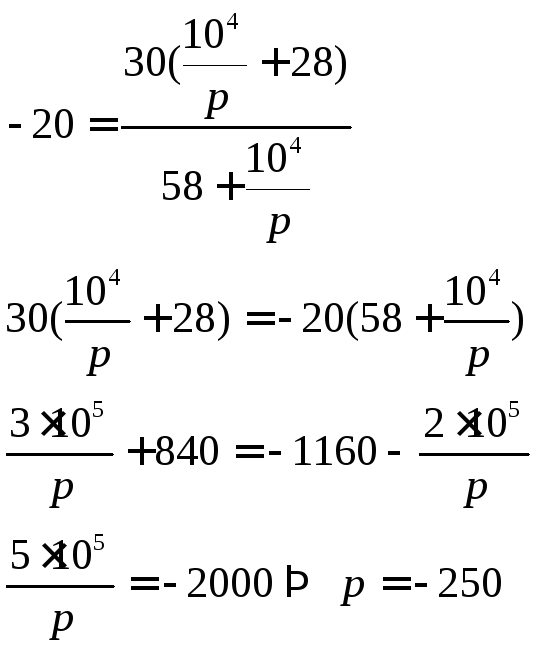
Цепь первого порядка процесс апериодический.

Определим напряжение на конденсаторе:

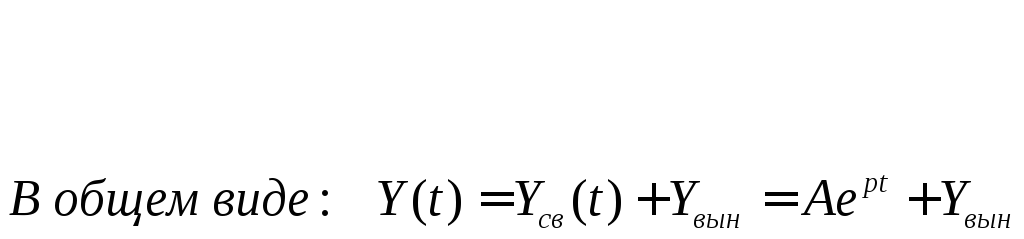
Переходные характеристики для входного тока и выходного напряжения:

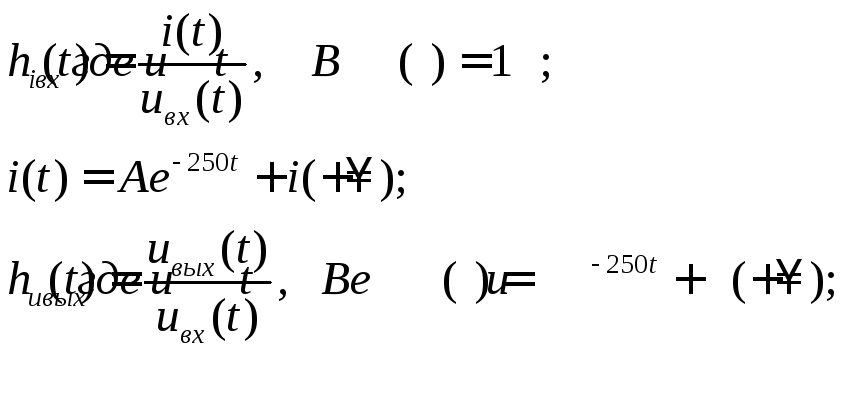
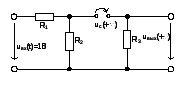
При t=+:

Рисунок 26. Схема четырехполюсника при t=+

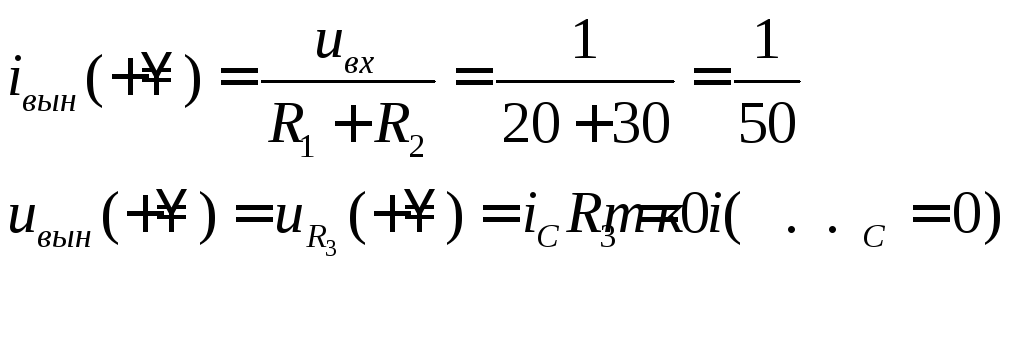
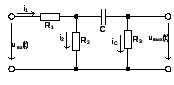
При t=+0:

Рисунок 27. Схема четырехполюсника при t=+0

Из законов коммутации:

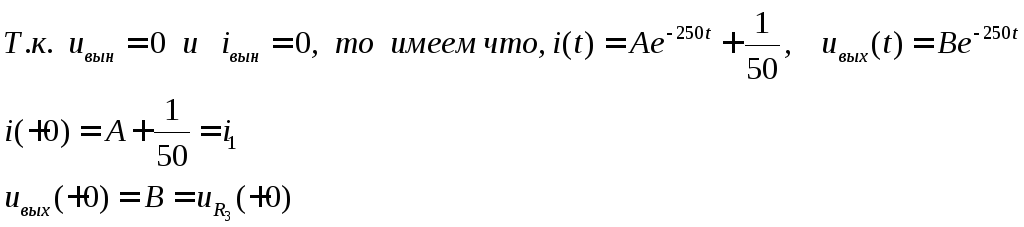
Далее представлены графики переходных и импульсных характеристик четырехполюсника.

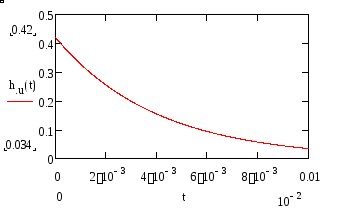
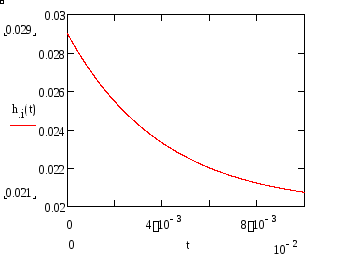
Рисунок 28. Переходная характеристика для выходного напряжения

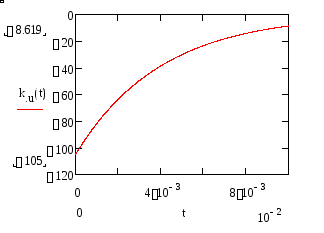
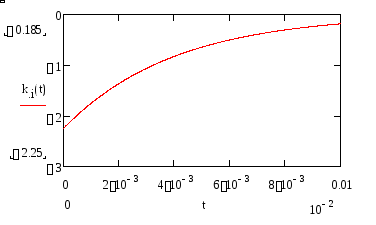
Рисунок 29. Импульсная характеристика для выходного напряжения

Рисунок 30. Переходная характеристика для входного тока

Рисунок 31. Импульсная характеристика для входного тока

4.2. Рассчитать и построить графики изменения входного тока и выходного напряжения четырехполюсника при подключении его к клеммам с напряжением в момент времениc учетом запаса энергии в элементах цепи от предыдущего режима работы на интервале , где Т-период изменения напряжения.

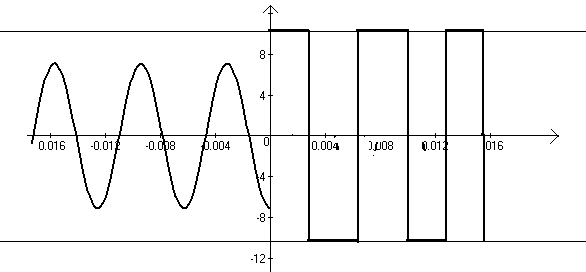
Рисунок 32. Входное напряжение до и после коммутации

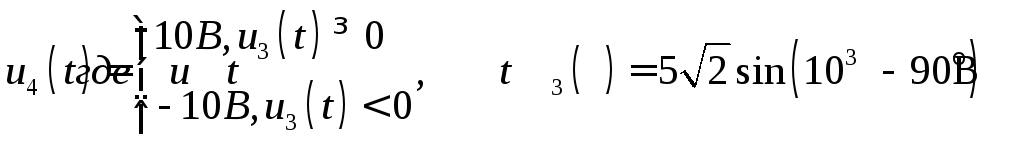
Найдем момент времени коммутации:

=0

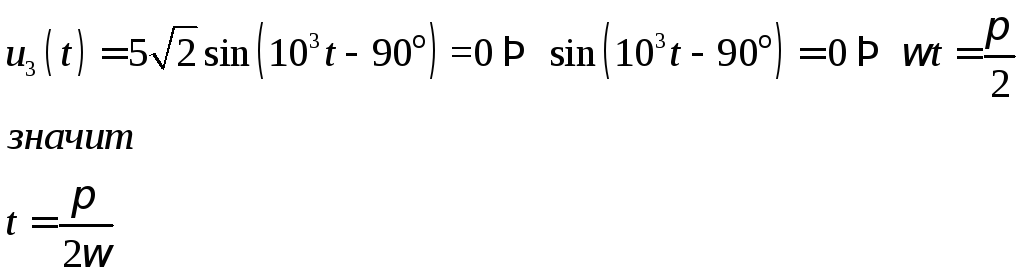
t – момент времени коммутации

Определим период изменения напряжения:

Учтем запас энергии на конденсаторе от предыдущего режима:

Вид характеристического уравнения аналогичен п.4.1 значит p=-250

Запишем общий вид зависимостей и:

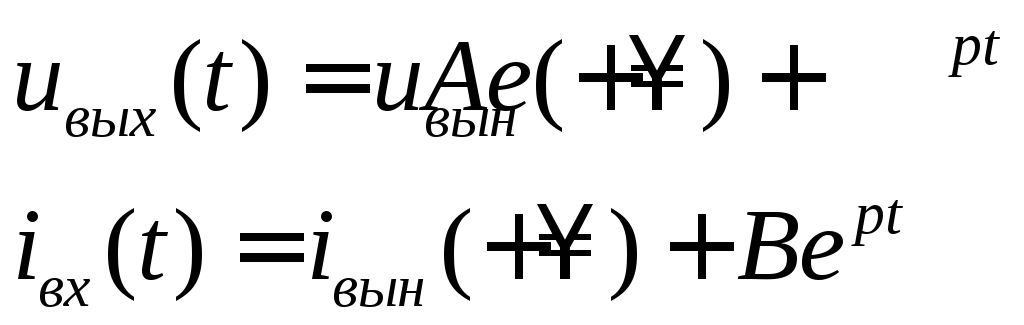
Рассчитаем и построим графики изменения входного тока и выходного напряжения на интервале , где Т-период изменения напряжения.

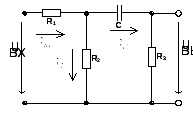
Рисунок 33. Схема четырехполюсника

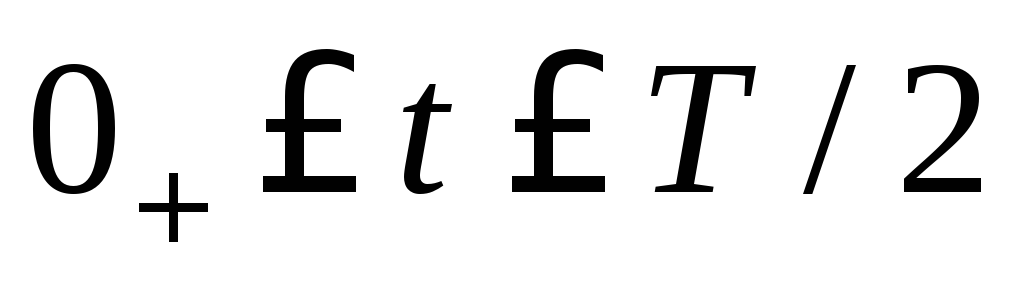1. , при

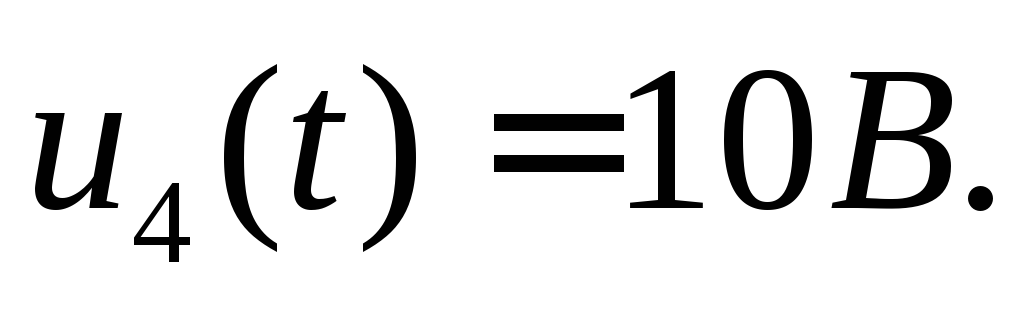
При t=+0:

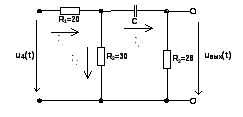
Рисунок 35. Схема четырехполюсника при t=+0

При t=+:

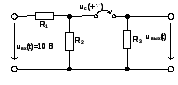
Рисунок 36. Схема четырехполюсника при t=+

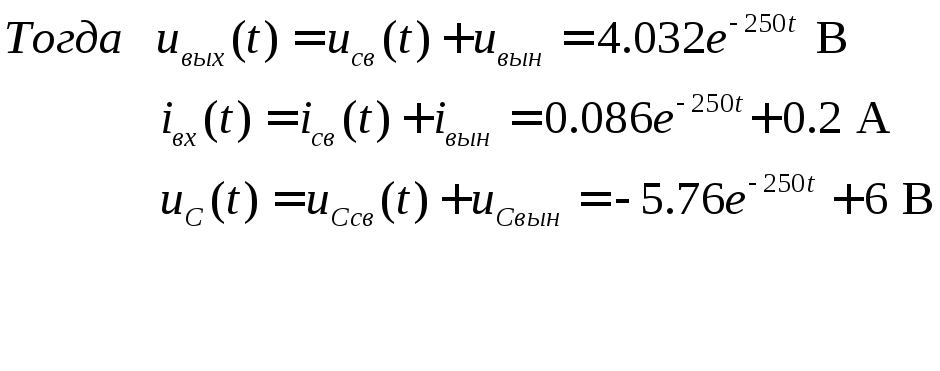
При

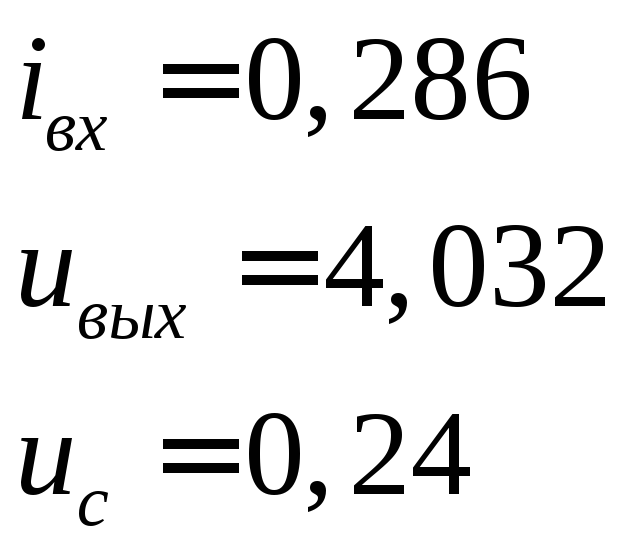
При

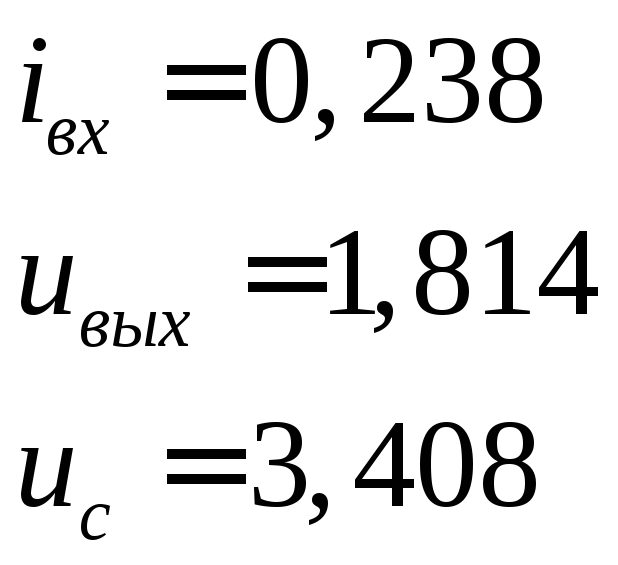
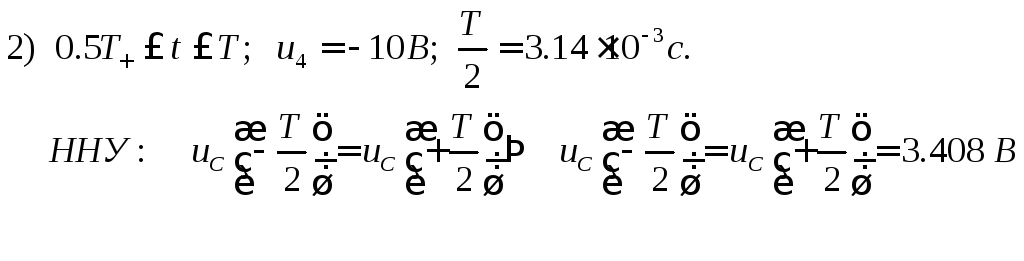
При

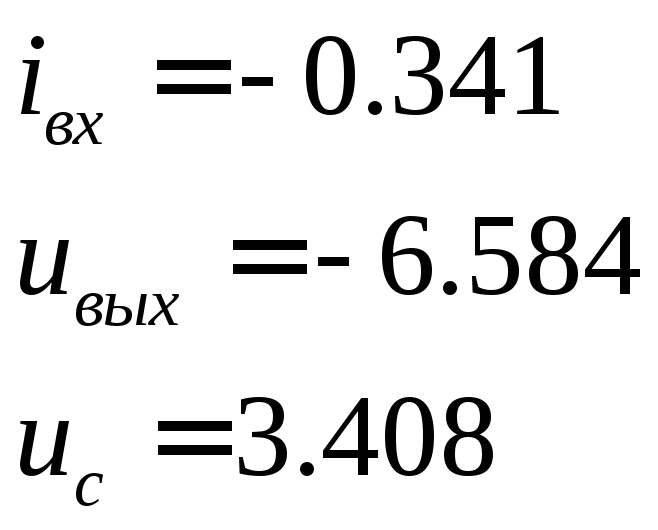
При

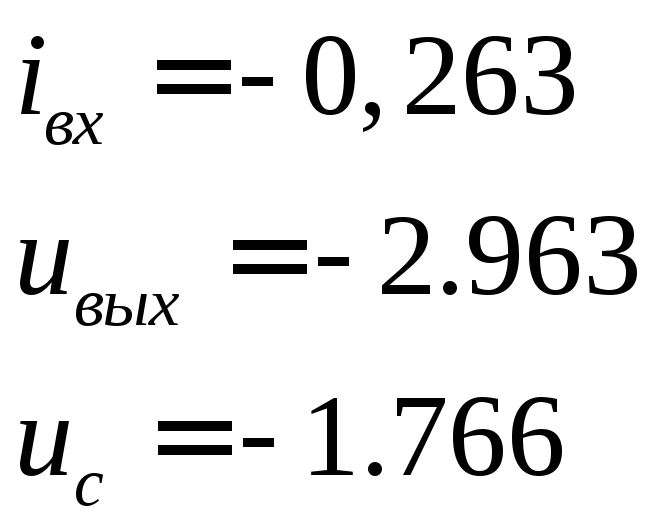
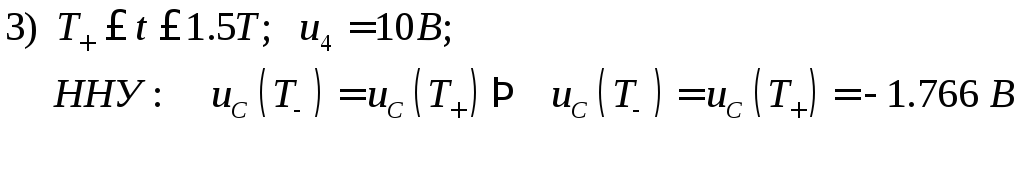
При

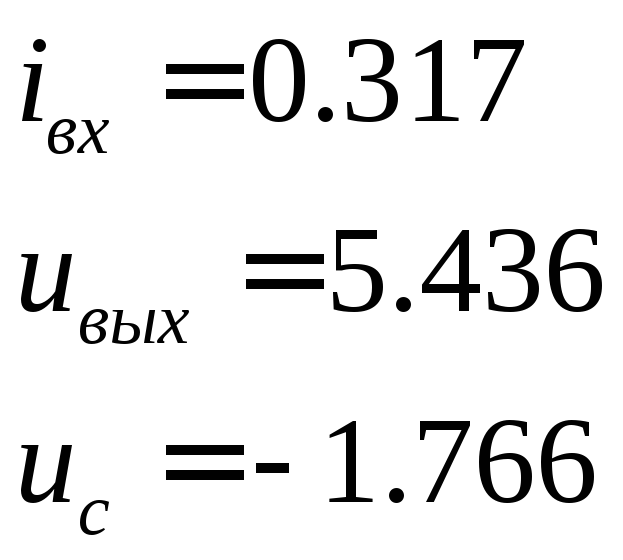
При

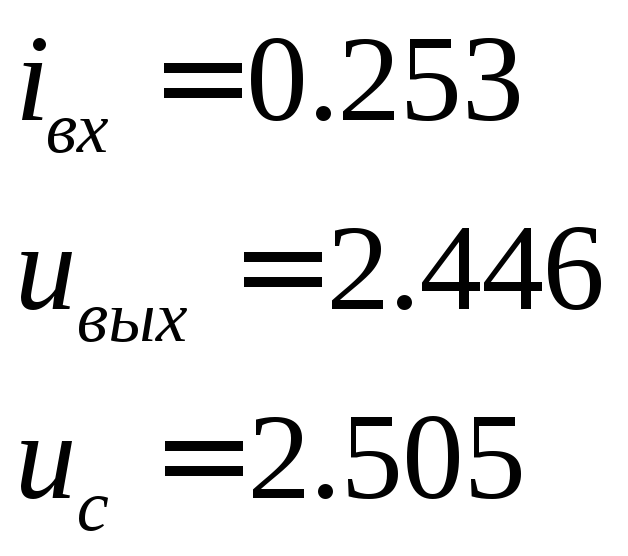
При

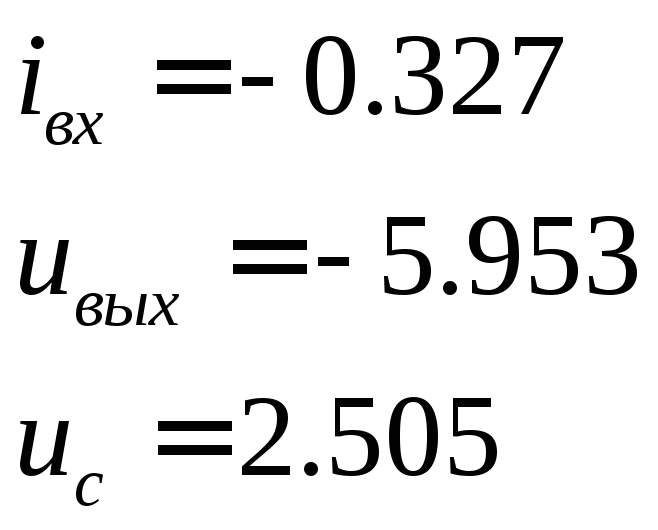
При

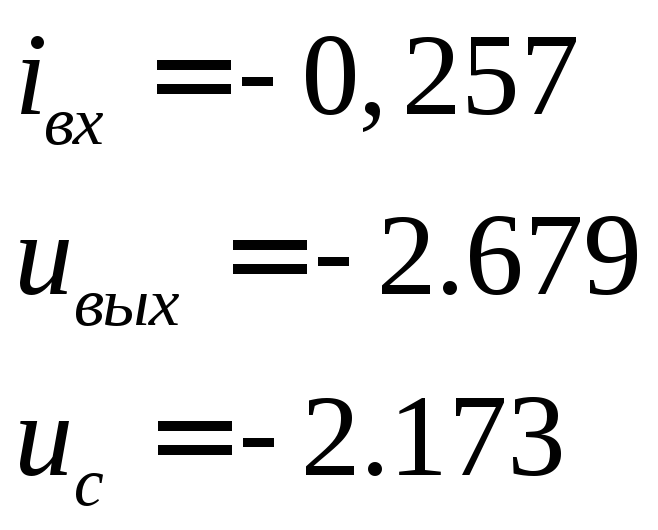
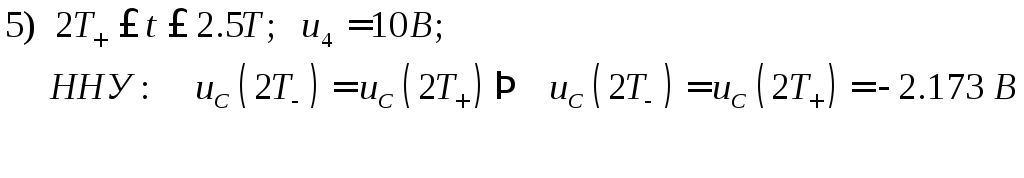
При

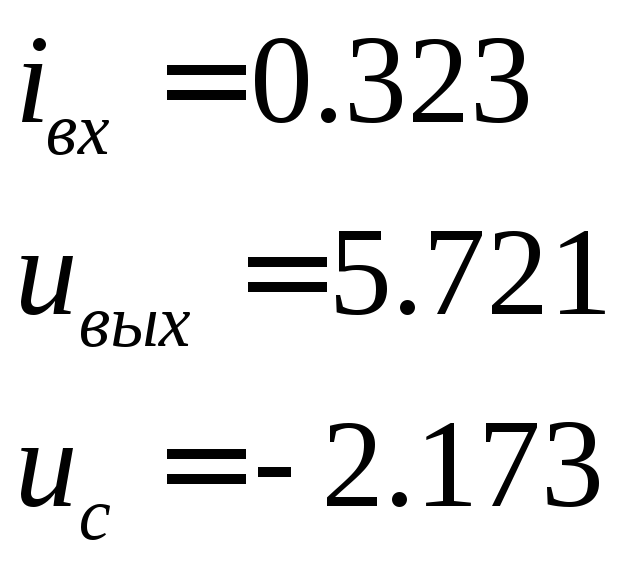
При

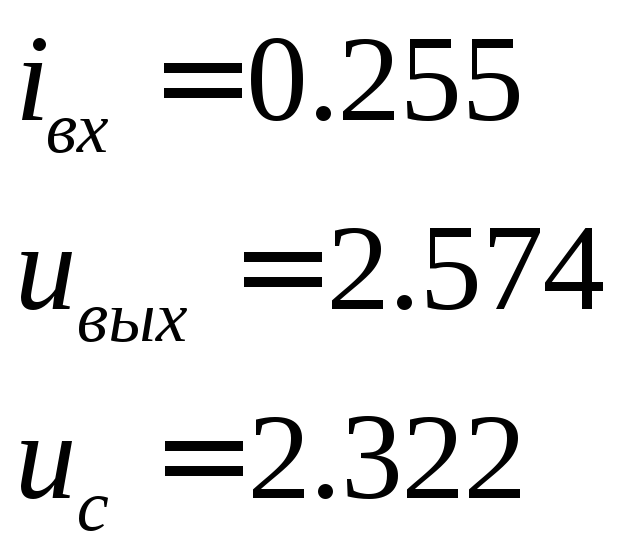
Построим графики ина:

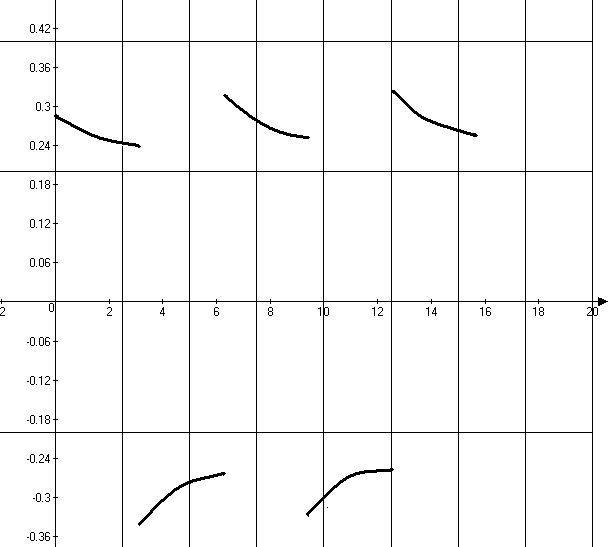
Рисунок 37. График входного тока на .

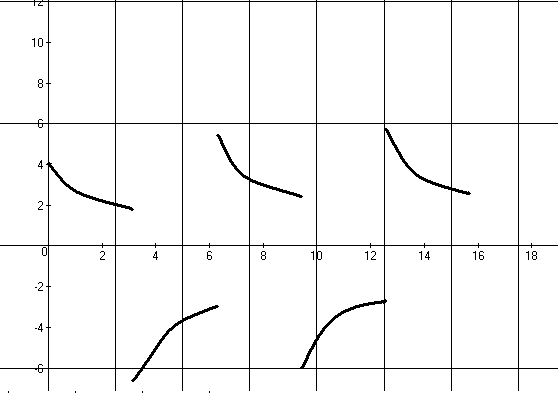
Рисунок 38. График выходного напряжения на .

Полученные графики практически совпадают с построенными в пункте 3.2.

Погрешность вызвана малым числом членов в разложении входного сигнала в ряд Фурье.

Выводы

В итоге проведенной работы были рассчитаны источник гармонических колебаний и четырехполюсник, являющихся элементами сложной электрической цепи.

Подтверждением правильности выполненных в курсовой работе расчетов является совпадение результатов, полученных в различных пунктах при использовании разнообразных методик.

При расчете тока в первичной обмотке трансформатора был получен результат(), а значение напряженияна первичной обмотке трансформатора опережает ток на угол, что верно.

Значения разности фаз () и отношения действующих значений выходного и входного синусоидальных напряжений () полностью совпадают со значениями, полученными из АЧХ и ФЧХ для частоты 1000 с^-1.

При разложении входного напряжения в ряд Фурье по 1, 3, 5-ой гармоникам получили: 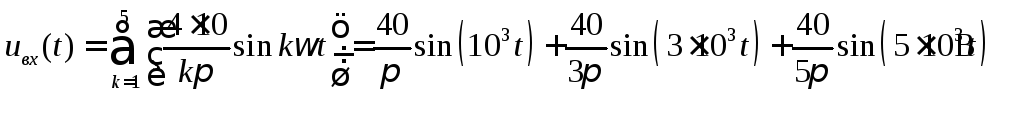. Полученное разложение будем тем точнее совпадать с прямоугольным импульсом, чем больше гармоник будет учитываться.

При нахождении выходного напряжения и входного тока частотным методом были получены следующие значения:

,

А.

Полученные фазы для различных частот (10³ с^-1, 310³ с^-1, 510³ с^-1) совпадают с ФЧХ четырехполюсника.

Из графика АЧХ четырехполюсника видно, что АЧХ достаточно стабильна на высоких частотах и сильно изменяется на низких. Такие изменения отражаются на зависимости выходного напряжения и входного тока от времени. Так, в то время, пока входное напряжение стабильно и равно 10 В или -10 В наблюдается спад в выходном напряжении и входном токе, что соответствует нестабильному участку с низкими частотами на АЧХ. И наоборот, в момент, когда входное напряжение скачком изменяется, так же скачком изменяются входной ток и выходное напряжение, что соответствует стабильному участку АЧХ.

Конденсатор заряжается первую половину периода, когда входной прямоугольный импульс положителен (u_вх(t)=10 B), и разряжается, когда входное напряжение отрицательно (u_вх(t) = -10 B). При этом, как и следует из законов коммутации, в момент скачка входного напряжения напряжение на конденсаторе изменяется плавно, без скачков.

Т.к. на элементах четырехполюсника происходит частичная потеря энергии, то происходит ослабление сигнала на 60% (поскольку W(10³)=0.407). Из-за того, что в цепи присутствует реактивный элемент, между выходным и входным напряжением возникает сдвиг по фазе, равный при частоте 10³ с^-1.