Лабораторный практикум по теории механизмов и робототехнике

Формулы (1.1) и (1.2) называются структурными формулами механизмов.

В механизмах с незамкнутыми кинематическими цепями число подвижных звеньев равно числу кинематических пар, и формула (1.1) принимает вид

W = р5 + 2р4 + 3р3 + 4р2 + 5р1,

т.е. число степеней подвижности такого механизма равно сумме степеней подвижности кинематических пар.

Так, для механизма манипулятора, показанного на рис. 1.6, а, имеем

W = р5 + 3р3 = 1+3·2 = 7.

Для механизма манипулятора, показанного на рис. 1.6, б,

W = р5+3р3 = 3+3 = 6.

Механизм манипулятора, приведенный на рис. 1.6, в, имеет

W = р5 = 4.

Такой же результат будет получен при подсчете числа степеней подвижности механизмов с незамкнутыми кинематическими цепями по фор-

муле (1.1).

Число степеней подвижности манипулятора при неподвижном захвате называется маневренностью манипулятора. Показанный на рис. 1.6, а манипулятор имеет одну степень маневренности, так как при неподвижном захвате его звенья могут вращаться вокруг оси, проходящей через центры сферических пар. Манипуляторы, показанные на рис. 1.6, б, в, не имеют маневренности, т.е. каждому положению захвата соответствует единственное расположение всех звеньев.

Для определенности движения всех звеньев механизма число степеней подвижности механизма должно соответствовать числу заданных независимых движений звеньев.

1.1.1.2. Принцип образования механизма

По методу Л. В. Ассура любой механизм может быть образован последовательным присоединением к входному звену и стойке структурных групп (групп Ассура). Входное звено со стойкой образуют так называемый механизм 1-го класса, или начальный механизм.

Структурной группой называется кинематическая цепь, которая после присоединения к стойке элементами внешних кинематических пар имеет нулевую степень подвижности.

Следовательно, структурная группа пространственного механизма должна удовлетворять условию

6n – 5р5 – 4р4 – 3р3 – 2р2 – р1 = 0.

Для структурной группы плоского механизма это условие имеет вид

3n – 2р5 – р4 = 0.

11

Для структурной группы плоского рычажного механизма это выражение еще упрощается: 3n – 2р5 = 0.

Отсюда следует, что число звеньев плоской структурной группы с низшимипарамивсегдачетное, ачислопаркратнотрем.

Простейшей и самой распространенной является группа второго класса, состоящая их двух звеньев и трех кинематических пар (одна внутренняя

идве внешние).

Взависимости от сочетания вращательных и поступательных пар структурные группы второго класса имеют 5 модификаций.

Ниже приведены схемы групп 2-го класса (группы Ассура) всех видов

имеханизмы, образованные присоединением этих групп ко входному звену

истойке (рис. 1.7, 1.8).

Рис. 1.7. Механизмы, образованные присоединением групп 2-го класса ко входному звену и стойке: а, б – шарнирный четырехзвенник; в, г, д – кривошипно-ползунный механизм; е, ж, з – кулисный механизм

На рис. 1.9. показана последовательность построения структурной схемы сложного механизма строгального станка. Он образован присоединением к кривошипу 1 и стойке структурной группы 2-го класса 3-го вида (звенья 2

12

Рис. 1.8. Тангенсный (а, б, в) и синусный (г, д) механизмы

и 3) и последующим присоединением к полученному кулисному механизму группы Ассура 2-го класса 2-го вида (звенья 4 и 5).

На рис. 1.10, а показана структурная группа 3-го класса 3-го порядка,

Рис. 1.9. Последовательность построения структурной схемы сложного механизма

а на рис. 1.10, б – группа 4-го класса 2-го порядка. Они весьма редко применяются в технике.

Кинематическая цепь, приведенная на рис. 1.10, в, имеет W = 0, но это не структурная группа, а соединение двух групп второго класса: (1 – 2) + (3 – 4).

13

Рис. 1.10. Структурные группы 3-го класса 3-го порядка (а), 4-го класса 2-го порядка (б), соединение двух структурных групп 2-го класса (в)

Попредложению И. И. Артоболевского классгруппыопределяется числом внутренних кинематических пар, входящих в наиболее сложный замкнутый контур.

Порядок группы определяется числом внешних кинематических пар, которыми группа присоединяется к механизму. Все структурные группы 2-го класса имеют 2-й порядок.

Присоединение к механизму или отсоединение от него структурной группы, т.е. кинематической цепи с нулевой степенью подвижности, не изменяет число степеней подвижности механизма, а значит, сохраняется определенность в движении звеньев механизма. Присоединение или отсоединение кинематической цепи с числом степеней подвижности, отличным от нуля, приведет к изменению числа степеней подвижности механизма, и при прежнем числе заданных независимых движений не будет определенности в движении выходных звеньев.

Класс и порядок механизма определяются высшим классом и высшим порядком структурных групп, входящих в состав механизма.

1.1.1.3. Эквивалент высшей кинематической пары

При изучении кинематических и динамических свойств плоских механизмов удобно заменять механизм с высшими кинематическими парами 4-го класса механизмом с низшими кинематическими парами.

Эквивалент высшей пары в плоском механизме можно найти путем сопоставления двух механизмов, у которых одно и то же число степеней подвижности и одинаковые законы движения звеньев.

Пусть в исходном механизме имеется одна высшая пара, в заменяющем – лишь пары 5-го класса.

Приравнивая выражения для W обоих механизмов, вычисленные по формуле (1.2), можно получить

3n − 2 p5 − p4 = 3n′− 2 p5′ .

Штрихи относятся к заменяющему механизму, отсюда

14

Равенство (1.3) превращается в тождество при p4 = 1; p5′– p5 = 2 и n′− n = = 1, т.е. заменяющий механизм по сравнению с исходным должен содержать одно дополнительное звено и две кинематические пары 5-го класса.

Рис. 1.11. Замена высшей пары одним звеном и двумя низшими парами

Чтобы звенья заменяющего механизма в рассматриваемом положении совершали такое же движение, как и звенья исходного механизма, необходимо соблюдать определенные правила замены высшей пары одним звеном и двумя низшими парами (рис. 1.11).

1.1.1.4.Избыточные связи

Внекоторых случаях подсчитанное по формуле (1.1) или (1.2) число степеней подвижности механизма оказывается меньше 1, но при соблюдении определенных условий сборки механизм обладает положительной подвижностью. Это свидетельствует о наличии в механизме избыточных связей, которые не влияют на движение звеньев и не учитываются при определении числа степеней подвижности механизма.

Так, если число избыточных связей в механизме q, то число степеней подвижности механизма с избыточными связями

Например, в механизме сдвоенного параллелограмма (рис. 1.12) подсчитанное по формуле (1.2) число степеней свободы W = 3·4 – 2·6 = 0.

Однако если AD//EF//BC и оси шарниров строго параллельны, то наличие звена 4 не вносит геометрических связей и число степеней подвижности механизма равно 1, как и в механизме без звена 4 (рис. 1.13). Звено 4 устанавливают для исключения превращения параллелограмма в антипараллелограмм при выходе из положений, в которых оси всех звеньев расположены на одной прямой.

При несоблюдении указанных геометрических соотношений число степеней подвижности механизма действительно равно нулю и движение звеньев невозможно.

Согласно формуле (1.2) в шарнирном четырехзвеннике (см. рис. 1.13) W = 1. Но если обусловленная неточностью изготовления непараллельность осей вращательных пар механизма не может быть компенсирована зазорами между элементами этих пар, то его следует рассматривать как пространст-

15

венный механизм. И тогда, согласно (1.4),число избыточных связей в этом механизме

q =1 – 6·3 + 5·4 = 3.

Сборка такого механизма возможна за счет деформации звеньев, а при его работе происходит усиленное изнашивание пар трения, появляется возможность заклинивания элементов кинематических пар.

Изменением подвижности кинематических пар можно устранить имеющиеся в механизме избыточные связи. Так, если в рассматриваемом шарнирном четырехзвеннике одну вращательную пару заменить сферической, а другую – сферической с пальцем либо одну вращательную пару заменить сферической, а другую – цилиндрической, то такие механизмы будут лишены избыточных связей. Для них

q = 1 – 6·3 + 5·2 + 4·1 + 3·1 = 0.

У кривошипно-ползунного механизма (см. рис. 1.2, б) устранить избыточные связи можно, например, заменой вращательной пары кривошип – шатун сферической, а поступательной – цилиндрической. Возможны и другие варианты устранения избыточных связей в рассмотренных механизмах.

Механизм без избыточных связей можно собрать без натягов при любых неточностях изготовления, что уменьшает силы трения в кинематических парах и увеличивает срок службы и надежность механизма. Такой механизм легко приспосабливается к деформации основания.

1.1.2.Порядок структурного анализа

1.Составить структурную схему механизма.

2.Определить число степеней подвижности механизма по формуле (1.2).

3.Заменить высшие пары низшими и определить число степеней подвижности заменяющего механизма по формуле (1.2).

4.Разложить механизм на структурные группы. Разложение следует начинать с отсоединения простейшей группы Ассура, наиболее удаленной по кинематической цепи от входного звена. При этом число степеней подвижности оставшейся кинематической цепи должно соответствовать числу степеней подвижности исходного механизма. Если отсоединить структурную

16

группу второго класса не удается, то следует отсоединить группу третьего класса и т.д. После отсоединения первой группы отсоединяют следующую группу и т.д.

В результате разложения остается одно входное звено со стойкой, если число степеней подвижности механизма равно единице. Если число степеней подвижности механизма равно k, то должно остаться k входных звеньев.

5.Записать формулу строения механизма, показывающую, в какой последовательности и какие группы Ассура присоединены к механизму первого класса.

6.Определить класс и порядок всего механизма.

1.1.3.Пример структурного анализа

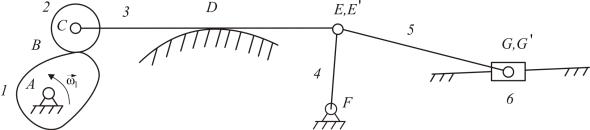
1.Структурная схема плоского механизма, представляющего замкнутую кинематическую цепь, показана нарис. 1.14.

2.Определим число степеней подвижности механизма по формуле (1.2):

W = 3n – 2p5 – p4.

Рис. 1.14. Плоский механизм замкнутой кинематической цепи (А, В, С, D, Е, E', G, G', F – кинематические пары)

Для данного механизма n = 6, p5 = 7, p4 = 2. В случае соединения нескольких звеньев (например в шарнире E) число кинематических пар определяется числом соединяемых звеньев, уменьшенным на единицу.

Так, в шарнире Е соединяются три звена: 3, 4, 5; следовательно, число кинематических пар здесь p5 = 2.

Таким образом,

W = 3·6 – 2·7 – 2 = 2.

Формально это свидетельствует о том, что для определенности движения всех звеньев механизма в нем должно быть два входных звена или одно входное звено с двумя заданными независимыми движениями.

Однако все звенья механизма совершают вполне определенное движение лишь при одном заданном движении одного из них (например кулачка 1). Лишнее число степеней подвижности механизма, получаемое при подсчете по формуле (1.2), обусловлено наличием ролика 2. Возможность вращения ролика 2 относительно стержня 3 не влияет на движение остальных звеньев механизма.

Если жестко закрепить ролик 2 на стержне 3, то при этом относительное движение остальных звеньев останется прежним, но число подвижных звеньев n и число кинематических пар 5-го класса p5 уменьшится на единицу (n = 5, p5 = 6), ачислостепенейподвижности механизма окажется следующим:

17

W = 3·5 – 2·6 – 2 = 1.

3. Заменяем высшие кинематические пары B и D механизма эквивалентными кинематическими цепями с низшими парами в соответствии со схемами, приведенными на рис. 1.11.

Рис. 1.15. Структурная схема заменяющего механизма

На рис. 1.15 приведена схема заменяющего механизма. Число степеней подвижности этого механизма

W = 3·7 – 2·10 = 1.

4.Разложим механизм на структурные группы. Разложение начинаем

сотсоединения простейшей группы Ассура, наиболее удаленной по кинематической цепи от входного звена. Это группа 2-го класса 2-го вида, содержа-

Если не удается отсоединить группу 2-го класса, то пытаются отсоединить группу 3-го или 4-го класса, состоящую из четырех звеньев и шести кинематических пар. Так, звенья 2, 3, 4 и 7 образуют структурную группу 3-го класса 3-го порядка (рис. 1.17).

В результате разложения остался механизм 1-го класса (входное звено со стойкой), имеющий W = 1 (рис. 1.18).

18

Таким образом, механизм, показанный на рис. 1.15, есть механизм 3-го класса 3-го порядка. Он образован последовательным присоединением к входному звену и стойке структурных групп 3-го класса 3-го порядка и 2-го класса 2-го порядка второго вида.

1.2.Применение числовых цепей

вструктурном анализе (второй метод исследования строения механизма)

Цель структурного анализа посредством числовых цепей – упроще-

ние строения механизма.

1.2.1.Теоретическая часть

Сточки зрения теории графов структурную схему механизма можно рассматривать в определенной степени как граф. Тогда, используя понятие цепи графа, можно наиболее просто решать ряд задач структурного анализа.

Понятие числовой цепи плоского механизма. Числовая цепь механиз-

ма – это последовательность, показывающая порядок соединения звеньев между собой. Стойка всегда обозначается цифрой 0, а входное звено 1. Например, числовой цепью механизма, или цепью механизма (рис. 1.19), является, последовательность вида

Рис. 1.19. Кинематическая цепь механизма

В этой цепи соединение звеньев во вращательную или поступательную кинематическую пару 5-го класса обозначается чертой, соединение в пару 4-го класса, т.е. высшую пару, – чертой со стрелкой (пара 1 →2).

Соединение более двух звеньев обозначается разветвленной чертой (узел 4 −−57 ). Цепь, начинающаясяснулейизаканчивающаяся ими, являетсязамкнутой.

Подсчет степени подвижности плоского механизма. На основании определения кинематической пары как подвижного соединения двух звеньев следует, что ее числовая цепь состоит из двух цифр (номеров звеньев)

19

и одной черты (пара 5-го класса) или черты со стрелкой (пара 4-го класса). Таким образом, общим числом кинематических пар 5-го класса в цепи механизма является число черт, 4-го класса – число черт со стрелкой. Числу подвижных звеньев соответствует число значимых цифр в цепи. Например, в механизме, показанном на рис. 1.19, число подвижных звеньев равно 8, кинематических пар 5-го класса – 11, а пар 4-го класса – 1. Степень подвижности механизма

W = 3n – 2p5 – 1p4 = 3·8 – 2·11 – 1 = 1.

До подсчета степени подвижности из структурной цепи механизма должны быть удалены пассивные связи и лишние степени свободы.

Замена в числовой цепи механизма кинематических пар 4-го класса.

класса и одним звеном. Например, цепь механизма, изображенного на рис. 1.19, до замены имеет вид

а после замены

Степень подвижности

W = 3n – 2p5 = 3·9 – 2·13 = 1.

Следовательно, замена правомерна.

Синтез сложных механизмов. Он производится на основании принципа Ассура. Числовая цепь структурной группы Ассура 2-го класса (рис. 1.20, а) независитотвидагруппы. Онасостоитиздвухзначащихцифритрехчерт.

Цепь группы Ассура 3-го класса (рис. 1.20, б) состоит из четырех значащих цифр и шести черт. В ней имеется цифра 3, связанная с тремя другими и являющаяся номером базисного звена в группе. Данную цепь нельзя разделить на двецепи2-гоклассабезразрывоввцепи.

Цепь группы Ассура 4-го класса (см. рис. 1.20, в) состоит из четырех значащих цифр и шести черт. Характерной особенностью является наличие замкнутого контура 2 - 3 - 4

└ 5 ┘

20