
Математические основы теории систем. Методы оптимизации
.pdf5. ОПТИМАЛЬНОЕ УПРАВЛЕНИЕ
Оптимальное управление – это частный случай задач вариационного исчисления. Решением этих задач является оптимальная функция управления объектом [6].
5.1. Постановка задачи
Дано:
1. Объект, описывающийся системой дифференциальных уравнений в фазовых координатах:
|
& |
|
|
|
|
|
|
= f1 (Y ,u,t), |
|
||||||
y1 |
|
||||||
|
|
... |
|
|
|
|
(5.1) |
|
& |
|
|
|
|
|
|
= fn (Y ,u,t), |
|
||||||
yn |
|
||||||
где yi |
– фазовые координаты (скорость, |
управление, |
путь), |
|||||||
|
|
|
|
|
|
& |
dyi |
|
|
|
|
|
|
|
|
|
|
|
|||
Y = (y1, y2 ,..., yn ,) – вектор фазовых координат, |
yi = |
|
, u |
= u(t) – |
||||||
dt |
||||||||||
|
|
|
|
|
|
|
|
|
||
функция управления. |
|
|
|
|
||||||
|
|
2. Целевая функция (обычно задается в виде определенного ин- |
||||||||
теграла) |
|
|
|
|
|
|
|
|||
|
|
|
T |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q = ∫G(Y |
,u,t)dt → min(max). |
|
|
|
(5.2) |
||
|
|
|
0 |
|
|
|
|
|
|
|
3.Начальные и граничные условия (всего 2n условий, n – порядок системы дифференциальных уравнений).
4.Ограничения на фазовые переменные: Bj(y1, y2,…,yп) ≤ 0,
j= 1,…,m.
5.Ограничение на управление: |u| ≤ 1, u – приведенный параметр управления.
131

Пример
Лифт управляется двигателем постоянного тока. Найти такое управление, при котором лифт доходил бы с одного этажа до другого за минимальное время.
Решение.
Управление осуществляется током якоря i =
рота якоря.
y1 = α , y2 = dα (угловаяскорость), u ≡ i, (функция dt
Система уравнений в фазовых координатах:
& |
= y2 , |
y1 |
|
& |
= u. |
y2 |
d2α , α – угол пово- dt2
управления– ток).
T
Целевая функция Q = ∫dt → min , T – время управления.
0
Граничные условия: у1(0) = – α0, у1(Т) = 0, у2(0) = 0, у2(Т) = 0. |u| ≤ 1 (ток управления лежит в некотором интервале (imin, imax)), α0 – угол, который должен отработать якорь двигателя.
5.2.Классификация задач оптимального управления
1.По виду целевой функции:
T
– задачи, оптимальные по быстродействию, Q = ∫dt → min ,
0
T
– задачи, оптимальные по расходу энергии, Q = ∫u2dt → min ,
0
–задачи, оптимальные по другим критериям.
2.По виду граничных условий:
–задачи с закрепленными концами (рис. 5.1), где начальное и конечное значения – точки на фазовой плоскости;
–задачи с подвижными концами (рис. 5.2), где вместо точек используются какие-либо поверхности.
132
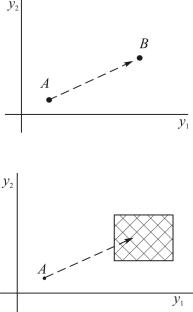
Рис. 5.1. Графическая иллюстарция задачи с закрепленными концами
Рис. 5.2. Графическая иллюстарция задачи с закрепленными концами
На рис. 5.1 А = (у1(0), у2(0)) – начальная точка, В = (у1(Т), у2(Т)) –
конечная точка. Задача заключается в нахождении такого управления, чтобы система перешла из А в В оптимальным образом (начальная точка считается левой, а конечная – правой).
Если конец подвижный, то граничные условия записываются следующим образом: уi(0) = у0i – координата начальной точки, φi(уi(T)) = 0 – конечное условие – поверхность, i = 1, …, п.
5.3. Принцип максимума Понтрягина
Принцип максимума Понтрягина позволяет найти оптимальное управление объектом.
Постановка задачи та же (5.1):
y& |
|
|
|
,u,t), |
||
= f (Y |
||||||
1 |
1 |
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
|
|
|
= fn (Y ,u,t), |
||||||
y&n |
||||||
|
133 |
|||||

T
Q = ∫G(Y ,t,u)dt → min.
0
Требуется найти u(t) – функцию управления объектом. Алгоритм принципа максимума Понтрягина
1. Введем переменную
t |
|
|
|
|
y0 (t) = ∫G(Y |
,t,u)dt. |
(5.3) |
||
0 |
|
|
|
|
Продифференцируем по времени y0 (t) : |
y0 = G(Y |
,t,u). |
||
|
|
|
& |
|
Добавим полученное дифференциальное уравнение к системе, описывающей объект:
|
& |
|
|
|
|
|
|
|
= G(Y ,t,u) ≡ f0 (Y ,t,u), |
||||||||
y0 |
||||||||
|
& |
|
|
|
|
|
|
|
|
= f1 (Y ,t,u), |
|||||||
y1 |
||||||||
|
|
(5.4) |
||||||
|
|
... |
|
|
|
|
|
|
|
& |
|
|
|
|
|
|
|
= fn (Y ,t,u). |
||||||||
yn |
||||||||
2. Составляем функцию Гамильтона
n
H = ψ0 f0 + ψ1 f1 + ... + ψn fn = ∑ψi fi ,
i=0
где ψi – неизвестные функции времени.
3. Находим ψi из системы дифференциальных уравнений:
ψi |
= − |
∂H , i = |
|
. |
(5.5) |
0,n |
|||||
dt |
|
∂yi |
|
||
4.Найденные ψi подставляем в Н.
5.Находим оптимальное управление u(t), исходя из следующего определения:
Принцип максимума Понтрягина: оптимальным является та-
кое управление u(t), при котором функция Гамильтона достигает максимума.
134
6. Найденное u(t) подставляем в систему дифференциальных уравнений фазовых координат (5.4). Находим фазовые координаты как функции времени.
Пример
Двигатель постоянного тока приводит в движение лифт. Найти такое управление лифтом, при котором лифт, переходя с одного этажа на другой, затрачивал бы минимум энергии.
Решение.
|
d2 y |
& |
|
u = |
|
|
, y1 = y, y2 = y1. |
dt2 |
|||
& |
= y2 |
, |
|
y1 |
|||
& |
= u. |
|
|
y2 |
|
||
T
Q = ∫u2dt → min,
0
граничные условия: у1(0) = – α0, у2(0) = 0, у1(Т) = у2(Т) = 0.
1. Составим систему дифференциальных уравнений в фазовых координатах:
y&0y&1y&2
=u2 ,
=y2 ,
=u.
2. Запишем функцию Гамильтона:
H= ψ0 f0 + ψ1 f1 + ψ2 f2 = ψ0u2 + ψ1 y2 + ψ2u.
3.Найдем функцииψi изсистемы дифференциальных уравнений:
|
|
|
∂H , |
|||
|
d |
ψ0 |
= − |
|||
|
||||||
dt |
|
|
∂y0 |
|
||
d |
|
|
∂H |
|
||
|
|
ψ1 |
= − |
∂y1 |
, |
|
|
||||||
dt |
|
|
|
|||
d |
|
|
∂H |
|
||
|
|
ψ2 |
= − |
∂y |
2 |
. |
|
||||||
|
|
|
|
|||
dt |
|
|
|
|
||
135

−∂H ∂y0
−∂H ∂y1
−∂H ∂y2
= 0 |
d |
ψ0 |
= 0 , следовательно, ψ0 = const = C0 . |
||
|
|||||
|
dt |
|
|
|
|
= 0 , |
d |
ψ1 = 0 , |
ψ1 = const = C1 . |
||
|
|||||
|
dt |
|
|
|
|
= −ψ1 |
, |
|
|
d |
ψ2 = −ψ1, ψ2 = C2 − ψ1t = C2 − C1t. |
|
|
dt |
|||
|
|
|
|
|
|
С учетом полученных ψi функция Гамильтона примет вид:
H= C0u2 + C1 y2 + (C2 − C1t)u.
4.Найдем управление, при котором функция Гамильтона дости-
гает максимума. Для этого найдем производную ∂H и приравняем
∂u
ее нулю:
∂H = 2C u + C − C t = 0,
∂ 0 2 1
u
u(t) = (C1t − C2 ) = K1t + K2 . 2C0
5. Подставляем найденное u(t) в систему дифференциальных уравнений в фазовых координатах:
y&2 = K1t + K2 ,
y2 = K1t2 + K2t + K3 , 2
y&1 = y2 = K1t2 + K2t + K3 , 2
y1 = K1t3 + K2t2 + K3t + K4 . 3 2
K1,…K4 находим из граничных условий: у1(0) = –α0, у2(0) = 0,
у1(Т) = = у2(Т) = 0.
5.4. Задача о максимальном быстродействии
Постановка задачи.
Задан объект управления п-го порядка, характеристическое уравнение которого имеет вещественные неположительные корни.
136

Ограничение на управление |u| ≤ 1. Цель управления – максимальное быстродействие:
T
Q = ∫dt → min.
0
Требуется найти u(t) – функцию управления объектом. Решение будем проводить для объекта второго порядка. Поло-
жим, объект описывается следующим дифференциальным уравнени-
ем: a0 &&y + a1 y& + y = u.
Составим характеристическое уравнение:
a0 p2 + a1 p + 1 = 0, |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
a |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
p2 + |
1 |
p |
+ |
|
|
|
|
= 0, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
a0 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
p1,2 = − |
|
|
a |
± |
|
|
a |
|
|
2 |
− |
1 |
= − A ± B, |
|
|||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||||
2a0 |
|
|
|
|
|
a0 |
|
||||||||||||||||||
|
|
|
|
|
|
2a0 |
|
|
|
|
|
|
|||||||||||||
где A = |
|
a |
|
B = |
|
a |
2 |
− |
1 |
|
|
||||||||||||||
|
1 |
|
, |
|
|
|
1 |
|
|
. |
|
||||||||||||||
|
|
|
|
|
2a0 |
|
|
|
|
|
|
|
2a0 |
|
|
a0 |
|
||||||||
Поскольку по условию задачи корни уравнения должны быть |
|||||||||||||||||||||||||
вещественными неположительными, то |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
1 |
|
|
|
|
|
|
|||||
A ≥ B и |
|
1 |
|
|
|
≥ |
|
|
. |
|
|
|
|
||||||||||||
|
|
|
|
|
|
a0 |
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2a0 |
|
|
|
|
|
|
|
|
|
= y, y 1 = |
|||||||
Применим принцип максимума Понтрягина. Пусть y1 |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
y2, подставим эти равенства в дифференциальное уравнение |
|||||||||||||||||||||||||
a0 y2 + a1 y2 + y1 = u . Выразим y2 : |
|
||||||||||||||||||||||||
|
& |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
& |
|
|
& |
= |
u − a1 y2 − y1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
y2 |
|
|
|
|
a0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Запишем систему дифференциальных уравнений в фазовых координатах:
137
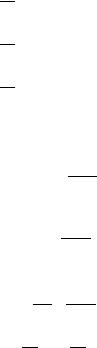
& |
= 1, |
|
|
|
|
|
|
|
||
y0 |
|
|
|
|
|
|
|
|||
& |
= y2 , |
|
|
|
|
|
|
|||
y1 |
|
|
|
|
|
|
||||
& |
= |
u |
− a1 y2 |
− y1 |
. |
|
|
|
|
|
y2 |
|
a0 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
2 |
|
|
u − a1 y2 − y1 |
|
|
Функция Гамильтона: H = ∑ψi fi |
= ψ0 + ψ1 y2 |
+ ψ2 |
. |
|||||||
|
||||||||||
|
|
|
|
|
i=0 |
|
|
a0 |
||
В функции Н только одно слагаемое зависит от и, следовательно, это слагаемое должно стремиться к максимуму. Предположим, что
ψ2 < 0, тогда из ψ2 |
u |
→ max следует и = –1; если же ψ2 > 0, то и = 1. |
|
||
|
a |
|
|
0 |
|
Таким образом и является знаковой функцией от ψ2.
Найдем функции ψi из системы дифференциальных уравнений:
d
dt
d
dtddt
ψ&1
ψ& 2
ψ0 |
= − |
∂H = 0, ψ0 = C0 , |
|||||
|
|
∂y0 |
|
|
|
||
ψ1 |
= − |
∂H = |
ψ2 |
, |
|
|
|
|
|
|
|
||||
|
|
∂y1 a0 |
|
|
|
||
ψ2 |
= − |
∂H = −ψ1 |
+ |
ψ2a1 |
= ψ2 . |
||
|
|||||||
|
|
∂y2 |
|
a0 |
|||
=ψ2 , a0
=−ψ1 + ψ2a1 . a0
Продифференцируем по t второе уравнение системы:
ψ&&2 = −ψ&1 + ψ& 2a1 . a0
Заменим ψ&1 согласно первому уравнению системы:
ψ&&2 = − ψ2 + ψ& 2a1 , a0 a0
ψ&&2 − a1 ψ& 2 + 1 ψ2 = 0. a0 a0
138

Составим характеристическое уравнение:
p2 − |
a1 |
p + |
1 |
|
= 0, |
|
|
|
|
|||
a0 |
a0 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
a |
|
|
a |
|
2 |
1 |
|
||
p1,2 |
= |
|
1 |
± |
|
1 |
|
− |
|
= A ± B. |
||
2a0 |
|
a0 |
||||||||||
|
|
|
|
2a0 |
|
|
|
|||||
Ранее было показано, что A ≥ B , следовательно, p1,2 ≥ 0 и функция ψ2 будет выглядеть следующим образом:
ψ2 (t) = C1ep1t + C2ep2t .
Если С1 и С2 положительны, то график ψ2 (t) пройдет выше оси абсцисс, если С1 и С2 отрицательны, график пройдет ниже оси абсцисс, если С1 и С2 имеют разные знаки, то график ψ2 (t) пересечет ось один раз. Таким образом, график ψ2(t) пересечет ось абсцисс не более одного раза, следовательно, функция управления сменит свой знак не более одного раза (количество переключений функции управления ≤ 1). По аналогии количество переключений функции управления объектом п-го порядка не превысит (п–1).
Теорема Фельдбаума об n интервалах
Для объекта n-го порядка, имеющего неположительные вещественные корни, оптимальное по быстродействию управление представляет собой кусочно-постоянную функцию, имеющую на интервале управления не более (n–1) переключения с одной границы допустимой области до другой.
Пример
Дан объект второго порядка, имеющий два нулевых корня. Найти оптимальное по быстродействию управление, при котором объект из любой точки фазовой плоскости переходил бы в начало координат за минимальное время.
Решение:
u = |
d2 y |
, |
|
u |
|
≤ 1, y (0) = y , |
y |
|
(0) = y |
|
, |
y (T ) = 0, |
y |
|
(T ) = 0. |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|||||||||||||
|
dt2 |
|
|
|
|
1 |
10 |
|
2 |
|
20 |
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||||||||
139

1.Уравнения в фазовых координатах:
|
& |
= 1, |
y0 |
||
|
& |
= y2 , |
y1 |
||
|
& |
= u. |
y2 |
||
2. Функция Гамильтона: H = ψ0 + ψ1 y2 + ψ2u .
|
|
|
∂H = 0, |
|
|
|||
|
d |
ψ0 |
= − |
|
ψ0 = C0 , |
|||
|
|
|||||||
dt |
|
|
∂y0 |
|
|
|
||
d |
|
|
∂H |
|
|
|
||
|
|
ψ1 |
= − |
∂y1 |
, |
|
ψ1 = C1, |
|
|
|
|||||||
dt |
|
|
|
|
|
|||
d |
|
|
∂H |
|
|
|
||
|
|
ψ2 |
= − |
∂y |
2 |
= ψ1 |
, |
ψ2 = C2 − ψ1t = C2 − C1t. |
|
||||||||
|
|
|
|
|
|
|||
dt |
|
|
|
|
|
|
||
u = sign ψ2 , где |
|
|
||||||
|
|
|
1, |
|
ψ > 0, |
|
||
sign ψ = |
|
|
ψ < 0. |
|
||||
|
|
|
−1, |
|
|
|||
u – кусочно-постоянная функция, которая переключается не более одного раза, т.е. либо и = 1, либо и = – 1.
Предположим, и = 1, тогда:
& |
= u = 1, |
|
||
y2 |
|
|||
y2 |
= t + K1, |
|
||
& |
= y2 = t + K1, |
|
||
y1 |
|
|||
y1 |
= |
t2 |
+ K1t + K2 = 0,5(t2 + 2K1t + K12 ) − 0,5K12 + K |
2 = |
|
||||
|
2 |
|
|
|
= 0,5(t + K1 )2 + S1 = 0,5y22 + S1.
Произвольно изменяя S1, можно построить семейство фазовых траекторий, соответствующих и = 1 (рис. 5.3). Стрелки на графиках указывают направление движения по траектории во времени. На-
правление определяется следующим образом: dy2 = u > 0 , следова- dt
тельно, с увеличением времени растет и значение координаты y2.
140
