223996

вывод, что два сорта яровой пшеницы статистически существенно не различаются по уровню урожайности.

Пример 6. На основании испытаний двух сортов яровой пшеницы в одинаковых условиях получены следующие данные.

Таблица 11 – Урожайность двух сортов яровой пшеницы

0,05 проверим нулевую гипотезу о равенстве средних урожайностей двух

сортов яровой пшеницы: Н0 : х y при Н1 : х y . Найдем выборочные средние и исправленные дисперсии по каждому сорту с помощью вспомогательной таблицы 12.

Таблица 12 – Вспомогательная таблица для расчета

21

Так как откорректированные выборочные дисперсии оказались неравные (3,09 и 2,22), то предварительно проверим нулевую гипотезу о равенстве генеральных дисперсий, используя F-критерий Фишера. Найдем отношение большей дисперсии к меньшей:

дисперсий принимается.

Для проверки нулевой гипотезы о равенстве двух средних независимых нормально-распределенных генеральных совокупностей с одинаковыми дисперсиями найдем наблюдаемое значение t-критерия

Стьюдента:

критическая область является двухсторонней. При уровне значимости

22

5.Дисперсионный анализ

Впрактике статистического анализа часто возникает вопрос –

насколько существенное влияние оказывает изменение одного или несколь-

ких факторов на изменение результативного признака. Для ответа на этот вопрос проводится дисперсионный анализ, сущность которого заключается в том, что дисперсия изучаемого признака разлагается на сумму составляющих её дисперсий (закон сложения дисперсий):

дисперсий, вызванных неучтёнными случайными причинами.

В дисперсионном анализе рассматривается гипотеза Н 0 – ни один из рассматриваемых факторов не оказывает влияния на изменчивость признака.

Алгоритм проведения расчетов:

1.Определяются необходимые суммы квадратов отклонений результативного признака, в соответствии с моделью дисперсионного анализа.

2.Находится число степеней свободы по каждому источнику вариации.

3.Рассчитываются средние квадраты отклонений.

4.Определяются наблюдаемые и критические значения критерия F-критерия Фишера, формулируются выводы относительно гипотезы Н 0 .

5.Оценивают значимость различий групповых средних по вариантам опыта.

Если Fнабл. > Fтабл. F, то делается вывод о существенности различий

результативного признака, обусловленных влиянием признака-фактора, т.е.

действие фактора на результативный признак признается статистически достоверным.

Пример 7. Оценить существенность различий в урожайности яровой пшеницы в зависимости от доз применяемых удобрений (табл. 13).

23

Таблица 13 – Урожайность яровой пшеницы в регионе

Рассчитаем суммы квадратов отклонений (табл. 14).

Таблица 14 – Вспомогательная таблица для расчета квадратов отклонений урожайности

24

урожайностей по дозам удобрений отвергается, т.е. влияние доз удобрений на урожайность озимой пшеницы является значимым.

Для оценки существенности частных различий в средней урожайности

вычисляем:

а) среднюю ошибку средней арифметической (среднюю ошибку

опыта):

Рассчитаем разность в средней урожайности по дозам удобрений, взяв за стандарт урожайность яровой пшеницы без применения удобрений.

Таблица 15 – Средняя урожайность по разным дозам удобрений, ц/га

Сравнивая полученные разности с HCP , видно, что они превосходят

25

HCP . Значит, исследуемые дозы удобрений дают значимую прибавку в сред-

ней урожайности озимой пшеницы по сравнению с первым вариантом.

6.Корреляционно - регрессионный анализ

Вэкономическом анализе первостепенное значение имеет выявление связей между явлениями. Связь между явлениями или отдельными признаками может быть многообразной. Один признак выступает как фактор,

другой как результат. Признак называется факторным, если он оказывает действие на другие признаки. Признак называется результативным, если он изменяется под влиянием фактора.

Многообразие связей классифицируется по следующим группам:

- Функциональные (полные) связи – такие связи, при которых значение результатов признака определяется значением факторного признака, т.е. при изменении в каждом отдельном случае фактора результат изменяется на строго определённую величину y f x , где x – фактор; y –

результат.

- Корреляционные (неполные) связи – связь, характеризующая взаимную зависимость двух случайных величин х и у, при этом изменение результативного признака (у) обусловлено не только влиянием факторного признака (х), но и прочих факторов ( ): y f x .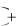

Корреляционно-регрессионный анализ – это совокупность статистико-

математических методов, используемых для количественного анализа связей

изависимостей между различными явлениями и процессами.

Взависимости, от числа признаков, между которыми изучается зависи-

мость, различают парную и множественную связь. Если изучается связь ме-

жду результативным признаком и двумя и более факторными признаками, то ока называется множественной.

При изучении связей между признаками устанавливают ее аналитиче-

ское выражение в виде линейного и нелинейного уравнения связи. Линейная

26

связь выражается уравнением y a bx , которое на графике имеет вид пря-

мой линии. При нелинейной зависимости применяются следующие функции:

параболическая, гиперболическая, степенная, показательная и другие.

Алгоритм проведения корреляционно-регрессионного анализа:

1.Определяется круг взаимодействующих факторов, показывающих влияние на результативный признак.

2.Для этой модели подбирается математическое уравнение, которое бы определило эту связь. Определяются параметры этого уравнения методом наименьших квадратов.

3.В прямоугольной системе координат на оси абсцисс откладывают значения факторного признака (х), на оси ординат – результативного (у).

На поле графика отмечают соответствующие индивидуальные значения признаков и по характеру их расположения судят о форме и направлении связи.

4.Производится оценка и анализ полученных результатов с использованием коэффициентов корреляции, детерминации, эластичности и других.

5.Определяются ошибки коэффициентов регрессии, а также их значимость.

6.Делаются выводы.

Параметры линейного уравнения (а и b) определяют путем составления и решения системы уравнений:

y an b х,

(20)

yх a х b х2 ,

Коэффициент регрессии (b) показывает, на сколько единиц в среднем изменяется результативный признак (у) при увеличении факторного признака (х) на единицу.

Коэффициент корреляции ( r ) характеризует направление и тесноту связи, он изменяется в пределах от -1 до 1. Если имеет место прямая связь, то

0 r 1, если обратная, то 1 r 0 . Коэффициент корреляции рассчитывается по формуле:

27

Теснота связи между результативным и факторным признаком оценивается по величине коэффициента корреляции.

Атрибутивная оценка тесноты корреляционной зависимости:

до 0,3 – слабая;

0,3 – 0,5 – умеренная;

0,5 – 0,7 – связь заметная;

0,7 – 0,9 – связь тесная;

0,9 – связь весьма тесная.

Возведя коэффициент корреляции в квадрат, и выражая результат в процентах, получают коэффициент детерминации:

Он показывает, на сколько процентов в среднем изменится результативный признак с изменением факторного на 1 %.

Пример 6. Проанализировать влияние на урожайность зерновых культур количества осадков за май, июнь на основании следующих данных

(табл. 16). Определить форму связи между признаками, параметры уравнения регрессии, тесноту связи между признаками, исчислить коэффициенты корреляции, детерминации и эластичности. Сделать выводы.

28

Решение. Урожайность зерновых культур зависит от количества осадков за май, июнь, поэтому факторным признаком является количество осадков за май, июнь, мм (х), результативным – урожайность с 1 га, ц (у).

Таблица 16 – Урожайность зерновых культур и количество осадков, выпавших в мае, июне

Проверку гипотезы о причинно-следственной связи между исследуемыми признаками начнем с графического метода, сущность которого заключается в построении корреляционного поля зависимости результативного признака (у) от факторного (х) (рис. 5).

ц/га

500

450

400

350

300

250

200

150

100

50

0

Рисунок 5 – Зависимость между урожайностью зерновых культур и количества осадков в мае, июне

29

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

На основании построенного поля можно сделать вывод о наличии прямой корреляционной зависимости между урожайностью зерновых культур и количеством осадков в мае, июне, поскольку наблюдается тенденция к увеличению из левого нижнего угла в правый верхний.

Расположение точек на графике показывает, что зависимость можно

выразить уравнением ~ y

Найдем параметры данного уравнения, составив систему уравнений,

используя данные таблицы 16 (колонки 4-6):

182,8 10а 3302в

62454,6 3302а 1139160в

Решив систему получим: а 25,41,в 0,132. Тогда уравнение связи

между урожайностью и количеством осадков примет вид: ~

y 25,41 0,132х .

Значит, при увеличении количества выпавших осадков в мае, июне на

1 мм, урожайность зерновых культур в среднем возрастает на 0,132 ц/га.

Рассчитаем коэффициент корреляции:

Таким образом, вариация урожайности зерновых культур на 44,09%

обусловлена вариацией количества выпавших в мае, июне осадков.

30