Расчет электрических цепей частотным методом (96

Московский государственный технический университет имени Н.Э. Баумана

С . И . Масленникова, Ю . Г . Шерстняков

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ЧАСТОТНЫМ МЕТОДОМ

Рекомендовано редсоветом МГТУ им. Н.Э. Баумана в качестве учебного пособия

Москва

Издательство МГТУ им. Н.Э. Баумана

2007

УДК 621.3(075.8) ББК 31.211

М 315

Рецензенты: О.И. Мисеюк, Ю.Н. Немов

Масленникова С.И., Шерстняков Ю.Г.

М 315 Расчет электрических цепей частотным методом: Учеб. пособие. — М.: Изд-во МГТУ им. Н.Э. Баумана, 2007.

— 44 с.: ил.

ISBN 978-5-7038-2992-9

В учебном пособии кратко изложены методы анализа электрических цепей при синусоидальных и несинусоидальных периодических воздействиях. На конкретных примерах показаны особенности применения методов анализа и порядок расчета. Приведен анализ цепей, содержащих магнитосвязанные индуктивные элементы, а также рассмотрены резонансные явления в электрических цепях.

Для студентов приборостроительных специальностей, выполняющих домашние задания по курсам «Теоретические основы электротехники» и «Теория электрических цепей». Также пособие может быть полезно при подготовке к рубежному контролю.

Ил. 31. Библиогр. 3 назв.

УДК 621.3(075.8) ББК 31.211

ВВЕДЕНИЕ

Электрической цепью называется совокупность соединенных определенным образом электромагнитных устройств, представляющих собой источники, потребители и преобразователи электрической энергии, электромагнитные процессы в которых могут быть выражены с помощью понятий тока и напряжения. В основе анализа цепей лежит принцип моделирования: реальное электромагнитное устройство заменяют идеализированной моделью, состоящей из взаимосвязанных идеализированных элементов, каковыми являются резистор, конденсатор, катушка индуктивности, катушки с магнитной связью, источники напряжения, ЭДС и тока. Схему этой электрической цепи, отображающей при определенных условиях свойства реальной цепи, называют схемой замещения. Часто термин «электрическая цепь» применяют к схеме замещения электрической цепи.

Электрическая цепь и соответственно ее схема имеют в общем случае ветви, узлы и контуры. Ветвь — участок цепи, в котором в любой момент времени протекает один и тот же ток; ветвь может содержать любое число последовательно соединенных элементов. Узел — место соединения трех и более ветвей. Простой узел — место соединения двух элементов. Контур — замкнутый путь, проходящий по одной или нескольким ветвям электрической цепи. Контур, не содержащий внутри других контуров, называют элементарным (ячейкой). Электрическую цепь называют плоской (планарной), если она может быть изображена в виде схемы с непересекающимися ветвями. Разветвленную цепь с источниками в различных ветвях считают сложной цепью.

Целью анализа электрической цепи с заданной структурой (схемой) и заданными характеристиками (параметрами) всех пассивных элементов является расчет токов при известных законах

3

изменения всех источников ЭДС, напряжения и тока, действующих в этой цепи. В данном пособии будут рассмотрены методы расчета установившихся режимов в сложных линейных электрических цепях, в которых источники являются синусоидальными функциями времени одной частоты.

Для расчета установившихся процессов в цепях синусоидального тока применяют комплексный метод. На основании этого метода получают комплексную схему замещения цепи из схемы для мгновенных значений заменой всех идеализированных пассивных элементов их комплексными сопротивлениями (проводимостями), всех независимых источников ЭДС, напряжения, тока — их комплексными изображениями. Для определения неизвестных комплексных изображений токов и напряжений можно использовать все методы расчета и преобразования электрических цепей с учетом алгебры комплексных чисел. При необходимости от комплексных изображений токов и напряжений переходят к их оригиналам.

Особенности расчета цепей несинусоидального тока рассмотрены в разд. 7.

1. ЗАКОНЫ КИРХГОФА, ФОРМИРОВАНИЕ СИСТЕМЫ УРАВНЕНИЙ

Провести расчет любой сложной цепи можно, составив по законам Кирхгофа систему независимых уравнений и решив ее. Число независимых уравнений должно быть равно числу неизвестных.

Положим, что схема состоит из p ветвей, s источников тока и q узлов. Заданными являются источники и пассивные элементы, а неизвестными — токи в ветвях. Таким образом, число независимых уравнений должно равняться числу ветвей n, не содержащих источников тока: n = p – s. При этом число независимых уравнений, составленных по первому закону Кирхгофа, будет равно n1 = = q – 1. Узлы, для которых уравнения записывают по первому закону Кирхгофа, можно назвать независимыми. В любой схеме число независимых узлов всегда равно q – 1.

По второму закону Кирхгофа, выражающему равенство алгебраической суммы ЭДС в контуре алгебраической сумме напряжений в нем, число независимых уравнений n2 = n – n1 = p – s – (q – 1).

4

Контуры, для которых уравнения составлены по второму закону Кирхгофа, называют независимыми. Независимый контур не содержит ветвей с источниками тока. В плоских схемах, не содержащих источников тока, число независимых контуров равно числу элементарных контуров.

Итак, расчет электрических цепей с помощью законов Кирхгофа сводится к составлению и решению n = n1 + n2 = (q – 1) + ( p –

– s – q + 1) = p – s независимых уравнений, что соответствует числу ветвей, не содержащих источников тока.

Решение системы уравнений возможно и в том случае, когда неизвестными являются некоторые входящие в схему источники. При этом необходимо, чтобы в качестве известных было задано такое же число токов. Общее число неизвестных не должно превышать n.

Пример 1.1. Для схемы (рис. 1, а) с известными значениями пассивных элементов и синусоидальных источников ЭДС и тока составить комплексную схему замещения, выразить характеристики всех пассивных элементов и источников в комплексной форме, составить систему независимых уравнений по законам Кирхгофа

для мгновенных и комплексных токов.

Положим, что e1 = Em1sin(ωt + ψ1), e5 = Em5sin(ωt + ψ5), e7 = = Em7sin(ωt + ψ7), iJ6 = Jm6sin(ωt + ψ6), а параметры пассивных эле-

ментов Rk, Lk, Ck указаны на схеме, где k — индекс (номер) элемента, соответствующий индексу ветви. Как правило, всем элементам, включенным в одну ветвь, присваивается один и тот же индекс. Для расчета цепи с помощью комплексного метода необходимо записать исходные данные в комплексной форме: E1 = ( E / 2 )×

+ jJ6sinψ6, Z1 = R1 + jωL1, Z2 = R2 – j/(ωC2), Z3 = R3 + jωL3 – j/(ωC3), Z4 = –j/(ωC4), Z5 = R5 – j/(ωC5), Z6 = R6, Z7 = 0, Z8 = R8 + jωL8 –

– j/(ωC8).

На рис. 1, б изображена схема с комплексными параметрами — комплексное изображение схемы рис. 1, а. Структура схем на рис. 1, а и б эквивалентна. Они состоят из восьми ветвей, одна из которых содержит идеальный источник тока, и пяти узлов. Для их расчета

5

необходимо составить по первому закону Кирхгофа n1 = q – 1 = 5 –

–1 = 4 уравнения, по второму закону Кирхгофа n2 = n – n1 = p – s –

–n1 = 8 – 1 – 4 = 3. Следовательно, в рассматриваемых схемах независимыми являются четыре узла и три контура. Независимые узлы и контуры можно выбирать произвольным образом. Полное число независимых уравнений n = n1 + n2 = 4 + 3 = 7.

Рис. 1

В качестве независимых узлов выберем узлы 1, 2, 3, 4, а независимые контуры обозначим криволинейными стрелками со знаком «плюс», задающими положительное направление обхода контура для составления уравнений: первый контур проходит по ветвям 1-2-7, второй — по ветвям 2-3-4, третий — по ветвям 4-5-8-7.

Система уравнений для мгновенных ЭДС, напряжений и токов схемы на рис. 1, а:

i1 – i2 – i3 = 0; i3 – i4 – i5 = 0; i5 – i6 – i8 = 0; i2 + i4 + i6 + i7 = 0;

R1i1 + L1di1/dt + R2i2 + 1/C2 i2dt = e1 – e7;

–R2i2 – 1/C2 i2dt + 1/C3 i3dt + R3i3 + L3di3/dt + 1/C4 i4dt = 0;

–1/C4 i4dt +R5i5 + 1/C5 i5dt + L8di8/dt +R8i8+1/C8 i8dt = e5+ e7.

Система уравнений для комплексов действующих значений ЭДС, напряжений и токов схемы на рис. 1, б:

I1 – I2 – I3 = 0; I3 – I4 – I5 = 0; I5 – I6 – I8 = 0; I2 + I4 + I6 + I7 = 0;

Z1I1 + Z2I2 = E1 – E7; – Z2I2 + Z3I3 + Z4I4 = 0;

– Z4I4 + Z5I5 + Z8I8 = E5 + E7.

6

Для расчета схемы на рис. 1, а необходимо решить систему из семи интегродифференциальных уравнений, а для расчета схемы рис. 1, б — систему также из семи уравнений, только алгебраических, что существенно проще. В этом заключается ценность метода комплексных амплитуд.

Положим, что в результате решения системы комплексных уравнений получены значения токов: I1 = a1 + jb1, I2 = a2 – jb2, I3 = = – a3 + jb3, I4 = – a4 – jb4, I5 = – a5, I7 = – jb7, I8 = jb8. Их аналога-

× sin(ωt + ψ5) = a5 2 sin(ωt ± π), i7 = Im7sin(ωt + ψ7) = a7 2 sin(ωt – π/2), i8 = Im8sin(ωt + ψ8) = a8 2 sin(ωt + π/2).

Трудность расчета сложных электрических цепей с синусоидальными источниками по законам Кирхгофа заключается в необходимости решать совместно n линейных алгебраических уравнений. Есть другие методы расчета сложных цепей, вытекающие из законов Кирхгофа, которые дают возможность уменьшить число независимых уравнений. Законы Кирхгофа непосредственно применяются в случаях, если:

–необходимо проверить правильность расчета, выполненного другими методами;

–необходимо определить напряжение между любыми точками рассчитанной схемы;

–в схеме есть магнитосвязанные контуры и магнитную связь нельзя заменить электрической;

–в схеме известна часть токов, но неизвестно такое же число ЭДС или сопротивлений.

2. МЕТОД КОНТУРНЫХ ТОКОВ

Метод контурных токов (МКТ) используют для упрощения расчетов. Он позволяет уменьшить число независимых уравнений

7

до числа независимых контуров n2 = n – n1 = p – s – (q – 1). МКТ основан на предположении, что в контурах схемы текут некоторые фиктивные токи, называемые контурными. Возможность разложения токов ветвей на контурные токи следует из принципа суперпозиции: ток в ветви равен алгебраической сумме контурных токов, протекающих в этой ветви. Уравнения, составленные для контурных токов по второму закону Кирхгофа, автоматически обеспечивают выполнение и первого закона Кирхгофа для узлов, так как контурные токи, проходя через узлы, остаются непрерывными, т. е. входят в узлы и из них выходят.

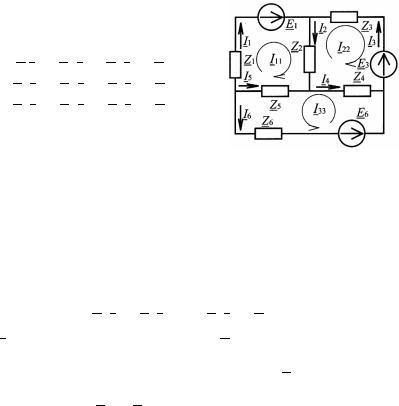
Пример 2.1. Поясним суть МКТ на примере расчета схемы электрической цепи (рис. 2) с тремя независимыми контурами. В схеме заданы комплексные значения источников ЭДС и сопротивлений. Необходимо составить систему уравнений по МКТ для определения токов ветвей.

Для формирования системы контурных уравнений необходимо выбрать систему независимых контуров. Для планарной схемы без источников тока независимыми контурами могут служить элементарные ячейки. В этой схеме их три — по числу независимых контуров: n2 = p – q + 1 = 6 – 4 + 1 = 3. Зададимся произвольно положительными направлениями контурных токов в этих контурах, как показано на рис. 2. Составим для этих контуров уравнения по второму закону Кирхгофа, принимая за положительное направление обхода контура положительное направление контурного тока:

(Z1 + Z2 + Z5)I11 – Z2I22 + Z5I33 = E1;

(Z2 + Z3 + Z4)I22 – Z2I11 + Z4I33 = – E3; (1)

(Z4 + Z5 + Z6)I33 + Z5I11 + Z4I22 = E6.

Так как контурный ток I22 не совпадает по направлению с I11 в общем для них сопротивлении Z2, то напряжение Z2I22 входит в уравнение со знаком «минус» (– Z2I22). Контурные токи I33 и I11 совпадают по направлению в общем для них сопротивлении Z5, и, следовательно, напряжение Z5I33 входит в первое уравнение со знаком «плюс». С учетом таких правил составлена система уравнений (1). Ее решение представляет стандартную вычислительную задачу линейной алгебры. Токи в ветвях равны алгебраической сумме контурных токов: I1 = I11, I2 = I11 – I22, I3 = – I22, I4 = – (I22 + + I33), I5 = – (I11 + I33), I6 = I33.

8

Запишем уравнения системы (1) в таком виде:

Z1I11 + Z12I22 + Z13I33 = E11;

Z21I11 + Z22I22 + Z23I33 = E22; (2)

Z31I11 + Z32I22 + Z33I33 = E33.

Получили так называемую каноническую форму записи уравнений в комплексной форме, которая позволяет добиться некоторого автоматизма при

записи системы уравнений. Эту форму можно распространить на любое число независимых контуров цепи, не содержащей источников тока:

Zb1I11 + Zb2I22 +...+ Zb3Ibb = Ebb,

где Ikk — контурный ток k-го контура; Ekk — алгебраическая сумма ЭДС ветвей, входящих в контур k: совпадающие с направлением контурного тока ЭДС берут со знаком «плюс»; Zkk — собственное сопротивление контура, равное сумме сопротивлений ветвей, входящих в контур k; Zkm = Zmk — общее сопротивление контуров k и m, причем сопротивления тех ветвей, контурные токи в которых совпадают по направлению, войдут в сумму со знаком «плюс», а в которых не совпадают — со знаком «минус».

Пример 2.2. Если электрическая цепь содержит также s источников тока, то для каждого источника следует выбрать свой контур, не проходящий через ветви с другими источниками тока. Контурный ток такого контура равен току источника, если он совпадает с ним по направлению. Эти контурные токи заданы, их не нужно определять. Для контуров, содержащих идеальные источники тока, нельзя составить уравнения по МКТ, так как их внутреннее сопротивление равно бесконечности и понятие собственного сопротивления такого контура лишено смысла. Следует помнить, что через ветвь с источником тока может протекать только один контурный ток, равный току источника с учетом знака.

9

Для независимых контуров уравнения составляют по обычным правилам. Число независимых уравнений равно p – s – q + 1, так как независимые контуры не содержат ветвей с источниками тока.

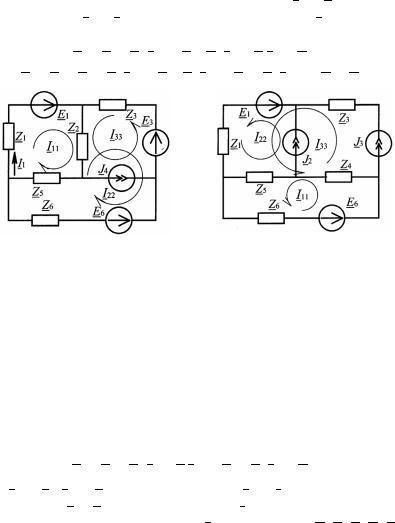
Рассмотрим схему с источником тока (рис. 3), в которой независимых уравнений два. Составим систему контурных уравнений, предварительно задавшись, как показано на рис. 3, направлениями контурных токов. При выбранном направлении I33 = J4. В уравнениях для токов I11 и I22 падение напряжения от тока I33 учитываем, как обычно:

(Z1 + Z2 + Z5)I11 – (Z2 +Z5)I22 + Z2I33 = E1;

(Z2 + Z3 + Z5 + Z6)I22 – (Z2 +Z5)I11 – (Z2 + Z3)I33 = – E3 – E6.

Пример 2.3. Рассмотрим выбор независимых контуров и составление уравнений для трехконтурной схемы с двумя независимыми источниками тока (рис. 4). Число независимых контуров в заданной схеме p – s – q + 1 = 6 –2 – 4 + 1 = 1, следовательно, необходимо составить всего одно уравнение для контура, не проходящего через ветви с источниками тока. Такой контур в схеме только один, он проходит по ветвям 4-5-6. Так как в ветви с источником тока должен протекать только один контурный ток, то одним из вариантов выбора контуров может быть схема на рис. 4. Уравнение для неизвестного контурного тока имеет вид

(Z4 + Z5 + Z6)I11 – Z5I22 – (Z4 + Z5)I33 = E6,

где I22 = J2, I33 = J3 — контурные токи; I22 и I33 совпадают по направлению с J2 и J3 соответственно. Ток I33, например, можно было направить по внешнему контуру, а I22 — по контуру E1-Z1-Z6-E6-Z4.

10