
Статистическая обработка экспериментальных данных (110
..pdf
линейный коэффициент корреляции, который характеризует степень тесноты линейной
зависимости rxy cov(x, y) . Коэффициент принимает значение в пределах от -1 до 1. Если
x y
с увеличением значения одного признака происходит увеличение второго, то говорят о прямой связи (например, увеличение роста человека ведет к увеличению веса тела), если с увеличением значения одного признака происходит уменьшение другого, то говорят об обратной связи (например, увеличение силы мышц приводит к уменьшению их подвижности). Степень варьирования значений одного признака при данном значении другого может быть различной. Если эта степень варьирования относительно мала, то связь близка к функциональной. Наименьшая частота связи соответствует случаю, когда варьирование обоих признаков осуществляется взаимно независимо. Качественная оценка тесноты связи величин X и Y может быть выявлена на основе шкалы Чеддока
|
|
Таблица 2. |
|
|
Шкала Чеддока |
|
|
Теснота связи |
Значение коэффициента корреляции при наличии: |
|
|
|
Прямой связи |
Обратной связи |
|
Слабая |
0,1-0,3 |
(-0,1)-(-0,3) |
|
Умеренная |
0,3-0,5 |
(-0,3)-(-0,5) |
|
Заметная |
0,5-0,7 |
(-0,5)-(-0,7) |
|
Высокая |
0,7-0,9 |
(-0,7)-(-0,9) |
|
Весьма высокая |
0,9-0,99 |
(-0,9)-(0,99) |
|
Часто для определения достоверности взаимосвязи между двумя признаками (Х, У)
используют непараметрический (ранговый) коэффициент корреляции Спирмена
 и параметрический коэффициент корреляции Пирсона
и параметрический коэффициент корреляции Пирсона  . Величина этих показателей корреляционной связи определяется по следующим формулам:
. Величина этих показателей корреляционной связи определяется по следующим формулам:
(1) где: dx — ранги статистических данных признака х; dy — ранги статистических данных признака у.
(2)
где:  — статистические данные признака х,
— статистические данные признака х,  — статистические данные признака у.
— статистические данные признака у.
Эти коэффициенты обладают следующими общими свойствами:
1.На основании коэффициентов корреляции можно судить только о прямолинейной корреляционной взаимосвязи между признаками. О криволинейной связи с их помощью ничего сказать нельзя.
2.Значения коэффициентов корреляции есть безразмерная величина, которая не может быть меньше -1 и больше +1, т.е. 
|
3. Если значения коэффициентов корреляции равны нулю, т.е. |
= 0 или |
= 0, то |
связь между признаками х, у отсутствует. |
|
|
|
|
4. Если значения коэффициентов корреляции отрицательные, т.е. |
< 0 или |
< 0, |
то связь между признаками Х и Y обратная. |
|
|
|
|
5. Если значения коэффициентов корреляции положительные, т.е. |
> 0 или |
y> 0 , |
то связь между признаками Х и Y прямая (положительная). |
|
|
|
|
6. Если коэффициенты корреляции принимают значения +1 или -1, т.е. |
= ± 1 |
|
или |
= ± 1, то связь между признаками Х и Y линейная (функциональная). |
|
|
21

7. Только по величине коэффициентов корреляции нельзя судить о достоверности корреляционной связи между признаками. Эта достоверность еще зависит от числа степеней свободы k .
k = n - 2, где: n — число коррелируемых пар статистических данных признаков Х и Y. Чем больше n, тем выше достоверность связи при одном и том же коэффициенте корреляции.
Кроме перечисленных общих свойств у рассматриваемых коэффициентов корреляции имеются и различия. Главное их отличие состоит в том, что коэффициент Пирсона ( ) может быть использован только в случае нормальности распределения
) может быть использован только в случае нормальности распределения
признаков Х и Y , коэффициент Спирмена ( ) может быть использован для признаков с любым видом распределения. Если рассматриваемые признаки имеют нормальное распределение, то целесообразнее определять наличие корреляционной связи с помощью
) может быть использован для признаков с любым видом распределения. Если рассматриваемые признаки имеют нормальное распределение, то целесообразнее определять наличие корреляционной связи с помощью
коэффициента Пирсона ( ), т.к. в этом случае он будет иметь меньшую погрешность, чем коэффициент Спирмена (
), т.к. в этом случае он будет иметь меньшую погрешность, чем коэффициент Спирмена ( ).
).
Для вычисления коэффициента корреляции по формуле Спирмена (1) требуется вычислять dx и dy ранги статистических данных, т.е. места вариант в их ранжированной совокупности. Если в совокупности несколько одинаковых данных, то их ранги равны и определяются как среднее значение от мест, занимаемых этими вариантами. Например,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Данные xi |
|
5 |
|
7 |
|
10 |
|
10 |
|
10 |
|
10 |
11 |
|
11 |
|
17 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
Ранги dx |
|
1 |
|
2 |
|
4,5 |
|
4,5 |
|
4,5 |
|
4,5 |
7,5 |
|
7,5 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
3 + 4 + 5 + 6 |
|
|
|
|
7 + 8 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Определить с помощью рангового коэффициента корреляции Спирмена существует ли взаимосвязь между результатами прыжка в длину с разбега (X в см) и конечной скоростью разбега (Y м/с) группы спортсменов
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
|
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
6 |
|
7 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xi ( см ) |
|
890 |
|
820 |
|
825 |
|
790 |
|
795 |
|
802 |
|
702 |
|
730 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
yi ( м/с ) |
|
10,7 |
|
10,5 |
|
10,1 |
|
9,8 |
|
10,1 |
|
10,5 |
|
9,1 |
|
9,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пользуясь правилом, определим ранги данных. Для удобства все запишем в виде таблицы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
Dy |
|
dx - dy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
702 |
|
1 |
|
9,1 |
|
1 |
|
1 |
- 1 = 0 |
|
02 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
730 |
|
2 |
|
9,6 |
|
2 |
|
2 |
- 2 = 0 |
|
02 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
790 |
|
3 |
|
9,8 |
|
3 |
|
3 |
- 3 = 0 |
|
02 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
795 |
|
4 |
|
10,1 |
|
4 |
|
4 |
- 4 = 0 |
|
02 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
802 |
|
5 |
|
10,5 |
|
6,5 |
|
5 |
- 6,5 = - 1,5 |
|
(- 1,5)2 = 2,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
820 |
|
6 |
|
10,5 |
|
6,5 |
|
6 |
- 6,5 = - 0,5 |
|
(- 0,5)2 = 0,25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
821 |
|
7 |
|
10,3 |
|
5 |
|
7 |
- 5 = 2 |
|
22 = 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
890 |
|
8 |
|
10,7 |
|
8 |
|
8 |
- 8 = 0 |
|
02 = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(dx-dy) = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
22

В данном случае имеем 8 пар значений, т.е. 8 коррелируемых пар. Значит n = 8. Подставив полученное в формулу (1), будем иметь:
Вывод:
а) Так как значение коэффициента корреляции положительное (0,92 > 0), то между признаками Х и У наблюдается прямая связь, т.е. с увеличением скорости разбега (признак У) увеличивается длина прыжка (признак Х), и наоборот — с уменьшением скорости разбега уменьшается длина прыжка.
Достоверность коэффициента корреляции Спирмена определяется по таблице критических значений рангового коэффициента корреляции  .
.
б) Так как полученное значение коэффициента корреляции  = 0,9 больше табличного
= 0,9 больше табличного
значений  = 0,88, соответствующего уровню b = 99%, то уверенность в правильности вывода (а) больше 99%. Такая достоверность позволяет распространить вывод (а) на всю генеральную совокупность, т.е. на всех прыгунов в длину.
= 0,88, соответствующего уровню b = 99%, то уверенность в правильности вывода (а) больше 99%. Такая достоверность позволяет распространить вывод (а) на всю генеральную совокупность, т.е. на всех прыгунов в длину.
Если не производится предварительной проверки рассматриваемых совокупностей на нормальность распределения, то, в случае недостоверности коэффициента корреляции Пирсона, следует проверить наличие связи еще и по коэффициенту Спирмена.
Пример 3. Предположим, что в нашем примере Xi и Yi— отвечают закону нормального распределения. Проверим наличие связи между результатами теста X и Y c помощью расчета нормированного коэффициента корреляции.
Из формулы (1) видно, что для вычисления  необходимо найти средние значения признаков X, Y и отклонения каждого статистического данного от его среднего
необходимо найти средние значения признаков X, Y и отклонения каждого статистического данного от его среднего
 . Зная эти значения, можно найти суммы
. Зная эти значения, можно найти суммы  по которым не сложно вычислить
по которым не сложно вычислить 
Используя данные задачи, заполним таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
3 |
|
4 |
|
5 |
|
|
6 |
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
890 |
|
96 |
|
962 |
= 9216 |
|
10,7 |
|
0,6 |
|
0,62 |
= 0,36 |
|
96 · 0,6 = 57,6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
820 |
|
26 |
|
262 |
= 676 |
|
10,5 |
|
0,4 |
|
0,42 |
= 0,16 |
|
26 · 0,4 = 10,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
821 |
|
27 |
|
729 |
|
|
10,3 |
|
0,2 |
|
0,04 |
|
|
5,4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
790 |
|
- 4 |
|
16 |
|
|
9,8 |
|
- 0,3 |
|
0,09 |
|
|
1,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
795 |
|
1 |
|
1 |
|
|
10,1 |
|
0 |
|
0,00 |
|
|
1,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
802 |
|
8 |
|
64 |
|
|
10,5 |
|
0,4 |
|
0,16 |
|
|
3,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
702 |
|
- 92 |
|
8464 |
|
9,1 |
|
- 1,0 |
|
1,00 |
|
|
9,2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
730 |
|
- 64 |
|
4096 |
|
9,6 |
|
- 0,5 |
|
0,25 |
|
|
32,0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 23262 |
|
|
|
|
|
= |
2,06 |
|
= 201 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
23

Подставив сумму столбца 7 в числитель формулы (2), а суммы столбцов 3 и 6 в знаменатель, получим:
r p |
x, y |
|
201 |
|
0.92 |
|
|
|
|
||||
23262 * 2.06 |
||||||
|
|
|
|
|
Вывод:
а) Так как значение коэффициента корреляции положительное (0.92>0), то между Х и Y наблюдается прямая связь, т.е. с увеличением скорости разбега (признак Y) увеличивается длина прыжка (признак Х) и наоборот — с уменьшением скорости разбега уменьшается длина прыжка.
По таблице критических значений нормированного коэффициента корреляции определим достоверность найденного коэффициента корреляции. Здесь число степеней свободы равно k = n - 2 = 8 - 2 = 6.
По таблице критических значений нормированного коэффициента корреляции для k = 6 величина  = 0,71 соответствует уверенности в 95% ( b = 100% - a ), а
= 0,71 соответствует уверенности в 95% ( b = 100% - a ), а  = 0,83 соответствует уверенности в 99%;
= 0,83 соответствует уверенности в 99%;
б) т.к. полученное значение коэффициента корреляции  = 0,94 больше табличного значения
= 0,94 больше табличного значения 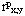 = 0,83, соответствующего уровню
= 0,83, соответствующего уровню  = 99%, то уверенность в правильности вывода (а) больше 99%. В области спорта такая уверенность достаточна, поэтому полученный вывод (а) можно распространять на всю генеральную совокупность (на всех прыгунов в длину).
= 99%, то уверенность в правильности вывода (а) больше 99%. В области спорта такая уверенность достаточна, поэтому полученный вывод (а) можно распространять на всю генеральную совокупность (на всех прыгунов в длину).
3.4.Уравнение регрессии
Впрактических исследованиях возникает необходимость аппроксимировать (математически описать приблизительно) корреляционную зависимость между двумя признаками уравнением. Для линейной зависимости сделать это относительно просто:
вытянутое корреляционное поле заменить усредненной прямой линией и найти ее уравнение по статистическим данным коррелируемых признаков. В прямоугольной системе координат уравнение прямой линии записывается в виде: 
Это математическое выражение корреляционной зависимости называется
уравнением регрессии. Коэффициенты a и b называются параметрами уравнения регрессии. Параметр а определяет на графике (рис.12) отрезок, отсекаемый графиком уравнения (прямой линией) на оси Y. Параметр b показывает, как изменяется признак Y при изменении признака X. Это "b " еще называют коэффициентом регрессии.
24

Рис. 12.
Уравнение регрессии тем лучше описывает корреляционную зависи мость, чем ближе она к линейной и чем больше ее достоверность. В случае нелинейной зависимости математически запись может выражаться в виде более сложных уравнений различных кривых линий (экспоненциальной кривой, параболы, гиперболы и т.д.).
При наличии достоверной криволинейной корреляционной зависимости можно подобрать уравнение, хорошо ее описывающее. Особенно эта возможность становится реальной при использовании специальных математических пакетов или электронных таблиц.
Определение уравнения прямолинейной регрессии
Как уже было сказано, в случае линейной зависимости уравнение регрессии является уравнением прямой линии. Таких уравнений два: (1)
(1)
 (2)
(2)
Если уравнение (1) называть прямым, то уравнение (2) будет ему обратным, и наоборот. Параметры  определяются на основании статистических данных признаков X и Y по формулам:
определяются на основании статистических данных признаков X и Y по формулам:
(3)
(4)
Коэффициенты регрессии имеют размерность, равную отношению размерностей изучаемых признаков X и Y, и тот же знак, что и коэффициенты корреляции.
 (5)
(5)  (6)
(6)
Чтобы вычислить , надо просто в уравнения (1) и (2) подставить средние значения коррелируемых признаков. Для оценки качества уравнения регрессии вычисляются остаточные средние квадратические отклонения по формулам:
, надо просто в уравнения (1) и (2) подставить средние значения коррелируемых признаков. Для оценки качества уравнения регрессии вычисляются остаточные средние квадратические отклонения по формулам:
25

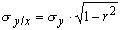 (7)
(7)
 (8)
(8)
Эти оценки абсолютны и, следовательно, не могут быть сравнимы друг с другом. Поэтому вводят оценки относительной погрешности уравнений регрессии, которые определяются в процентах по формулам:
 (9)
(9)
 (10)
(10)
Значение этой оценки, если r = ± 1,00, равно нулю, и, если r = 0,00, максимально. Остаточное среднее квадратическое отклонение характеризует колеблемость y относительно линии регрессии по x, и наоборот в обратном случае.
Пример 4. Найти уравнения регрессии для веса (Х) и роста (Y) группы студентов, если их значения таковы:
Решение:
1. Занесем результаты тестирования в рабочую таблицу:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
60 |
|
-11 |
|
121 |
|
170 |
|
-10 |
|
100 |
|
110 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
65 |
|
- 6 |
|
36 |
|
168 |
|
-12 |
|
144 |
|
72 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
71 |
|
0 |
|
0 |
|
180 |
|
0 |
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
73 |
|
2 |
|
4 |
|
182 |
|
2 |
|
4 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
75 |
|
4 |
|
16 |
|
189 |
|
9 |
|
81 |
|
36 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
80 |
|
9 |
|
81 |
|
190 |
|
10 |
|
100 |
|
90 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
72 |
|
1 |
|
1 |
|
178 |
|
-2 |
|
4 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 259 |
|
|
|
|
|
= 433 |
|
= 314 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. Рассчитаем нормированный коэффициент корреляции по формуле:
;
 .
.
3. Подставим полученные данные в уравнения регрессии:
26

.
Тогда уравнение регрессии примет вид:
Т.е.  (1)
(1)
 (2)
(2)
4. В конечные значения уравнений (1) и (2) подставим произвольные значения показателей x и y (например, 1-го исследуемого).
Тогда:
5. Разобранную в данном примере корреляционную зависимость можно представ ить графически в виде, приведенном на рисунке 13, учитывая следующие особенности данного представления:
две линии уравнения регрессии на графике пересекаются в точке M с координатами средних значений показателей x и y;
чем ближе коэффициент корреляции по своему значению к |1|, тем меньше угол между линиями на графике. При r=± 1 линии уравнения регрессии либо совпадают, либо расположены параллельно, так как корреляционная взаимосвязь между
признаками в этом случае переходит в функциональную;чем ближе значение коэффициента корреляции к нулю, тем больше угол между
линиями на графике. При r=0 линии уравнения регрессии на графике расположены перпендикулярно, т.е. взаимосвязь между показателями отсутствует
27

Рис. 13.
4. Понятие статистической гипотезы
Статистические выводы – это заключения о законе распределения исследуемой случайной величины и его параметрах, либо о наличии и силе связи между исследуемыми переменными на основе выборки, случайно отобранной из генеральной совокупности.
Обобщение результатов, полученных по выборке, на генеральную совокупность есть суть статистических выводов.
Статистической называют гипотезу о виде закона распределения или о параметрах известного распределения.
В 1-ом случае гипотеза называется непараметрической, во-втором – параметрической.
Гипотеза, подлежащая проверке, называется нулевой (основной) Н0, это гипотеза об отсутствии различий, например, уровень (качество) чего-либо одинаковый (ое).
Гипотеза о значимости различий – это Н1 – альтернативная.
Пример. В эксперименте участвуют две группы спортсменов. Перед экспериментом группы не имеют различий, то есть спортсмены приблизительно равны по антропометрическим и физическим качествам и одинаково подготовлены. Контрольная группа тренируется по традиционной методике, вторая (экспериментальная) по экспериментальной. Насколько эффективна новая методика можно оценить по различию результатов, показанных спортсменами этих групп после определенного тренировочного цикла. Для оценки достоверности различий в результатах применяются различные методы сравнения. Например, выдвигаются статистические гипотезы: нулевая и альтернативная.
Но – среднее значение результатов не изменилось. Если заранее нельзя сказать, к чему приведет использование новой методики, то альтернативная гипотеза Н1 будет состоять в том, что средние значения генеральных совокупностей неодинаковы. Если можно предположить, что использование новой методики приведет к увеличению (уменьшению результатов), то альтернативная гипотеза Н1 записывается с помощью знаков « >», « <».
Гипотезу называют простой, если она содержит одно конкретное предположение и сложной, если она состоит из конечного или бесконечного числа простых гипотез.
Процедуру сопоставления высказанной гипотезы с выборочными данными называют проверкой статистической гипотезы. Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются или нет данные наблюдений и выдвинутая гипотеза.
При проверке гипотеза принимается или отклоняется.
Но отклоняется в том случае, когда вероятность того, что она верна, оказывается ниже некоторого уровня, называемого уровнем значимости.
28
Уровень значимости – наибольшее значение вероятности, несовместимой со случайностью события или это максимум таких вероятностей, при которых событие можно считать практически невозможным.
Р=1- - уровень достоверности.
Наиболее употребительные уровни =0,001(0,1%); 0,01(1%); 0,05(5%).
Уровень значимости, выраженный в % показывает, сколько раз в 100 испытаниях мы рискуем ошибиться, объявив изучаемой событие неслучайным. Например, 5% уровень значимости допускает ошибку в 5 случаях из 100.
При анализе гипотез возможны следующие ошибки:
Но отвергается, когда она верна (ошибка первого рода);
Но принимается, когда верна Н1 (ошибка второго рода).
Снижая уровень значимости, мы уменьшаем вероятность ошибки первого рода, но при этом возрастает вероятность ошибки второго рода. Поэтому вводится понятие мощности критерия, которая представляет собой вероятность отклонении Но.
5. Статистические критерии
Статистикой называется любая функция выборочных значений. Для проверки правдоподобия нулевой гипотезы используют специально подобранную статистику, закон распределения которой известен. Такая статистика называется статистическим критерием К.
Статистические критерии – это решающее правило принятия истинной и отклонения ложной гипотезы с указанной вероятностью.
Для проверки правдоподобия статистической гипотезы с помощью критерия К назначается уровень значимости , по которому находится критическое значение критерия – Ккрит. Область значения критерия разбивается числом Ккрит. на две части: критическую область и область принятия гипотезы.
Критической областью называется совокупность значений критерия, при которых нулевую гипотезу отвергают.
Областью принятия гипотезы называется совокупность значений критерия, при которых нулевую гипотезу принимают.
Пусть f(X,Q) – закон распределения случайной величины X с некоторым параметром
Q.
В случае, когда Н1 формулируется в виде Q=Q0, используется двухсторонний критерий.
Если Н1 формулируется в виде Q>Q0 (или Q<Q0) используется односторонний критерий.
Параметрическими являются критерии, включающие в формулу расчета параметры распределения, то есть среднее, стандартное отклонение, дисперсию и пр. (t- критерий Стьюдента, критерий F Фишера и др.). Параметрические критерии можно применять только в том случае, когда изучаемый признак подчиняется нормальному закону распределения.
Непараметрические критерии основаны на оперировании частотами или рангами (критерий Вилкоксона, критерий знаков, критерий Манна Уитни и др.)
Проверка гипотез обычно проходит следующие этапы:
1.Определение используемой статистической модели. Выдвижение предположений относительно закона распределения случайной величины и его параметров. Например, закон распределения нормальный, величины независимы и пр.
2.Формулирование гипотез Н0 и Н1
3.Выбор уровня значимости α в зависимости от требуемой надежности выводов.
4.Определение критической области для проверки Но. Вид этой области (одностороння или двусторонняя) зависит от принятой Н1. Основной принцип проверки
29
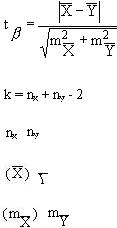
правдоподобия статистической гипотезы формулируется так: если наблюдаемое значение критерия Кнабл. принадлежит критической области – гипотезу отвергают, если же наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают, то есть считают, что полученные выборочные статистики не противоречат сформулированной гипотезе.
5.Вычисление значения выбранного статистического критерия Кнабл. для имеющихся данных
6.Сравнение Кнабл. с Ккрит. (табличным). Принятие решения.
6. Сравнение групп методом Стьюдента
Метод Стьюдента применяется для сравнения двух выборок, взятых из одной и той же генеральной совокупности, или двух различных состояний одной и той же выборочной совокупности.
При этом могут представиться следующие случаи:
1. По объему:
а) обе группы большие (n>30); б) обе группы малые  ;
;
в) одна — большая, вторая — малая.
2. По составу:
а) группы с попарно-зависимыми вариантами, когда i-тая варианта первой группы сравнивается с i-той вариантой второй группы (nx=ny);
б) группы с попарно-независимыми вариантами (можно менять варианты местами внутри группы).
Исходя из таких условий задачи могут быть трех типов:
I. Сравнение двух больших (или одной большой, одной малой) групп с попарнонезависимыми вариантами проводится по формулам:
|
|
(1), |
|
|
(2), где: k — число степеней свободы, |
, |
— соответственно объемы первой и второй выборки, |
|
, |
|
— средние арифметические соответственно 1 и 2 группы, |
|
, |
— ошибка репрезентативности соответственно 1 и 2 группы, |
 — критерий Стьюдента, по найденному значению которого определяют доверительную вероятность различия групп.
— критерий Стьюдента, по найденному значению которого определяют доверительную вероятность различия групп.
II. Сравнение двух малых групп с попарно-независимыми вариантами проводится по формулам:
30
