Статистическая обработка экспериментальных данных (110

2.Медиана. Медианой (Ме) называется такое значение признака Х, когда одна половина значений экспериментальных данных не меньше ее, а вторая половина

– не больше.

Если данных немного, то медиана вычисляется просто – данные ранжируют и находят значение, стоящее посередине. Т.е. ранг (порядковый номер) медианы

вычисляется так – RMe n 1 . 2

Пример 2.

а) n=9: 12, 14, 14, 18, 20, 22, 22, 26, 28.

Ранг медианы равен RMe 9 1 5 , Ме=20

2

б) n=10: 6, 8, 10, 12, 14, 16, 18, 20, 22, 24.

число между 14 и 16 (5 и 6 членом ряда). Принято считать в качестве медианы среднее арифметическое этих значений, т.е. Ме=(14+16)/2=15

Если надо найти медиану для сгруппированных данных, то сначала находят интервал группировки, в котором содержится медиана. Медианным будет тот интервал, в котором накопленная частота впервые окажется больше n/2 (n – объем выборки) или накопленная частость – больше 0.5.

Внутри медианного интервала медиана определяется по формуле:

Для приведенного выше интервального вариационного ряда (пример 2,п.1.4) медиана находится в интервале 182-188, которому соответствует накопленная частота 11.

По формуле: Ме=182+6*(20*0.5-9)/11=182,5.

Определив медиану, мы нашли, что в группе испытуемых по прыжкам в высоту одна половина показала результат лучше 182,5 см, а другая – хуже.

Для тех случаев, когда эмпирической распределение оказывается сильно ассиметричным, среднее арифметическое теряет свою практическую ценность, в этой ситуации медиана представляет собой лучшую характеристику центра распределения.

3. Мода (Мо). Мода представляет собой значение признака, встречающееся в выборке наиболее часто. Интервал группировки с наибольшей частотой называется

модальным.

Для определения моды используется формула:

nMo nMo 1

Мо=хМон+h (nMo nMo 1) (nMo nMo 1) ,

где хМон – нижняя граница модального интервала, h – ширина интервала,

-частота модального интервала,

-частота интервала, предшествующего модальному,

-частота интервала, следующего за модальным.

Для данных таблицы (пример 2,п.1.4) имеем:

Мо=188+6*(9-2)/((9-2)+(9-0))=190,6 (см)

11

То есть наибольшее число прыгунов в группе показали результат близкий к 190.6

см.

Сравнивая для выборки из примера 2 (п.1.4) значения среднего арифметического, медианы и моды (184,1; 182,5; 190,6 соответственно), видим, что они отличаются, что свидетельствуют о несимметричности распределения данных.

2.2. Характеристики рассеяния (варьирования) данных

Рассмотренные данные не дают полной информации о варьируемом признаке. Например, средние значения могут быть одинаковы, а значения признака – рассеяны в различном диапазоне.

Колеблемость (изменчивость) признака позволяют оценить такие статистические величины как

размах варьирования,

дисперсия,

среднее квадратическое отклонение и

коэффициент вариации.

1.Размах варьирования определяется как разность между наибольшим и наименьшим результатом измерений, т.е. измеряет на числовой прямой расстояние, в

пределах которого изменяются оценки: R=Xmax-Xmin. Для данных примера 2 (п.1.4)

R=194-170=24.

2. Дисперсия ()

Дисперсия – это средний квадрат отклонения значений признака от среднего

интервала.

Значение дисперсии для примера 2 (п.1.4) :

=(3*(173-184)+6*(179-184)+2*(185-184)+9*(191-184))/19=44

3. Среднее квадратическое (или стандартное) отклонение.

Основной мерой статистического измерения изменчивости признака у членов совокупности служит среднее квадратическое отклонение (сигма) или, как часто ее называют, стандартное отклонение. Теория вариационной статистики показала, что для характеристики любой генеральной совокупности, имеющей нормальный тип распределения достаточно знать два параметра: среднюю арифметическую и среднее квадратическое отклонение. Эти параметры заранее не известны и их оценивают с помощью выборочной средней арифметической и выборочного стандартного отклонения, которые вычисляются при обработке случайной выборки.

12

Стандартным отклонением (средним квадратическим отклонением) называется квадратный корень из дисперсии:

Значение стандартного отклонения для примера 2(п.1.4) : σ=6,63 (см) Свойства стандартного отклонения:

1.Стандартное отклонение всегда σ измеряется в тех же единицах измерения, что и основные варианты.

2.Чем больше σ, тем больше изменчивость признака.

3.В вариационных рядах с нормальным распределением частот 99,7% всех членов совокупности отстоят от средней арифметической на величину от

. За пределами находятся только 0,3% всех членов совокупности.

4. При вычислении стандартное отклонение определяют с точностью на один десятичный знак больше, чем точность, которую применяют для вычисления средней арифметической для того же ряда.

Согласно 1-му свойству стандартное отклонение характеризует степень отклонения результатов от среднего значения в абсолютных единицах. Однако для сравнения колеблемости двух и более совокупностей, имеющих различные единицы измерения, эта характеристика непригодна. Для этого используется относительный показатель – коэффициент вариации.

4. Коэффициент вариации (V) вычисляется по формуле .

Это отношение стандартного отклонения к среднему арифметическому, выражается в процентах. Чем больше V, тем более изменчив признак. Считается, что если V<=10% то выборку можно считать однородной, т.е. полученной из одной генеральной совокупности. Если V>20%, то выборка некомпактна по заданному признаку. Колеблемость (изменчивость) результатов измерений в зависимости от величины коэффициента вариации считают небольшой (до 10%), средней (11-20%) и большой (более 20%). Коэффициент вариации используется как показатель однородности выборочных наблюдений.

Для данных примера 2(п.1.4) V=6,63/184,1=0.036 (3.6%). Это значение меньше 10,

репрезентативности - характеризует колебания средней. При этом необходимо отметить, что чем больше объем выборки, тем меньше разброс средних величин.

Стандартная ошибка средней вычисляется по формуле:.

В современной научной литературе средняя арифметическая представляется вместе с ошибкой репрезентативности: .

Пример 4.

Определить основные статистические показатели результатов прыжка в длину группы спортсменов, если данные выборки таковы:

xi, см ~ 185, 171, 190, 170, 190, 178, 188, 174, 193, 178, 176, 180, 175, 176, 180, 192 (n=16).

13

Решение:

1. Для вычисления основных статистических показателей составим рабочую таблицу следующего вида:

2.Для определения среднего арифметического используем формулу:

3.Для вычисления стандартного отклонения определяем разности и заносим во 2 столбец. Находим квадраты этих разностей, записываем их в 3-ий столбец и

рассчитываем Тогда:

4. Определим ошибку репрезентативности по формуле:

5. Определим стандартную ошибку среднего арифметического, используя формулу:

Х181 1,9см

6.Определим коэффициент вариации по формуле:

14

Выводы: 1) среднее значение высоты прыжка составляет 181 см;

2) по показателю высоты прыжка группа компактна, т.к. стандартное отклонение составляет ± 7,6 см, а коэффициент вариации — 4, 2 % (менее 10%).

2.3. Кривая нормального распределения

При анализе распределения результатов измерений всегда делают предположение о том распределении, которое имела бы выборка, если бы число измерений было очень большим. Такое распределение (очень большой выборки) называют распределением генеральной совокупности или теоретическим, а распределение экспериментального ряда измерений — эмпирическим.

Теоретическое распределение большинства результатов измерений описывается формулой нормального распределения, которая впервые была найдена английским математиком Муавром в 1733 г.:

Это математическое выражение распределения позволяет получить в виде графика кривую нормального распределения (рис.1), которая симметрична относительно центра группирования (обычно это значение моды или медианы). Эта кривая может быть получена из полигона распределения при бесконечно большом числе наблюден ий и интервалов. Заштрихованная область графика на рис.1 отражает процент результатов измерений, находящихся между значениями х1 и х2.

Рис. 5. Кривая нормального распределения

Введя обозначение , которое называется нормированным или стандартизованным отклонением, получают выражение для нормированного распределения.

15

2.4. Точечное и интервальное оценивание числовых характеристик

Точечной оценкой числовой характеристики называют оценку, которая определяется одним числом. К точечным оценкам относятся, например, среднее арифметическое, стандартное отклонение. Если выборка небольшого объема, то точечная оценка может значительно отличаться от оцениваемого параметра и ее использование может привести к грубым ошибкам. В этом случае используют интервальные оценки числовой характеристики. Интервальной оценкой числовой характеристики называется интервал, который с доверительной вероятностью p (задаваемой заранее) накрывает истинное значение числовой характеристики генеральной совокупности.

Доверительная вероятность – это уровень гарантии суждения о значениях генеральной характеристики на основании выборочных данных. Чаще всего p=0,95 (95%).

Вероятность α=1-р того, что построенный доверительный интервал не накроет значение генеральной совокупности, называется уровнем значимости, или вероятностью ошибки.

Образцы решения задач Задача 1. Дан ряд чисел 4,4,4,5,5,6,6,6,6,7,8,8,9,9,9, Найти среднее, моду, медиану,

размах варьирования, стандартное отклонение, коэффициент вариации этого ряда чисел. Что характеризует каждый из этих показателей?

Решение.

Для расчета воспользуемся формулами

Задача 2. В ходе опроса 30 студентов было выявлено, сколько времени в среднем ежедневно (час) они затрачивают на подготовку к занятиям. Получены следующие данные (варианты):

2,3,4,2,4,3,3,3,4,2,2,3,4,3.5,4,3.5,4,2.5,4,3.5,4,4,5,4,3.5,4,3,4,4,2.5

16

Определить сколько времени в среднем тратят студенты на подготовку к занятиям. Определить моду, медиану, размах варьирования, стандартное отклонение, коэффициент вариации. Каков практический смысл показателей?

Решение.

Упорядочим данные по возрастанию, построим для них дискретный ряд распределения

Для вычисления среднего значения можно использовать сгруппированные данные и использовать формулу для вычисления взвешенной средней арифметической в дискретном ряду распределения

Среднее время Тср.=(2*4+2,5*2+3*6+3,5*4+4*13+5*1)/30≈3,4(час)

Ме=3,5, Мо=4, размах варьирования 5-2=3, стандартное отклонение 0,78, коэффициент вариации 23%.

3,4 часа – это среднее слагаемое, около которого колеблются все остальные значения ряда данных, мода (4 часа) показывает наиболее типическое значение времени на подготовку к занятиям, медиана (3,5 часа) – время подготовки, которое не превосходит время подготовки у половины опрошенных студентов, размах варьирования (3 часа) показывает наибольший разброс времени на подготовку к занятиям, стандартное отклонение – абсолютный разброс времени относительно среднего, коэффициент вариации – относительный разброс времени относительно среднего и показывает в данном случае, что рассматриваемый признак – время на подготовку к занятиям - варьирует сильно(20%<23%<30%).

3. Основы корреляционного и регрессионного анализа

3.1. Функциональная и корреляционная зависимости

В природе многие явления и процессы взаимосвязаны между собой. В организме человека тоже существует много взаимосвязей между различными признаками. Например, с повышением интенсивности нагрузки повышается пульс, увеличивается скорость кровотока в работающих мышцах, уменьшаются в них энергетические ресурсы; регулярность тренировок, оптимально подобранные нагрузки по их виду, объему и интенсивности улучшают результаты спортсмена и т.д.

Влияние одних признаков на другие может быть положительным и отрицательным. Грамотный специалист должен хорошо разбираться в таких взаимосвязях в своей области, устранять или уменьшать негативное влияние и уметь своевременно и в достаточной мере использовать полезные взаимосвязи.

Некоторые методы математической статистики могут помочь любому специалисту выявить взаимосвязи, раскрыть их особенности. Одним из таких методов и является метод корреляционного анализа. Он направлен на то, чтобы на основе статистического материала выявить факт влияния одного признака на другой, установить полезность или вред этого влияния и оценить уверенность в полученных выводах. При этом различают два вида зависимости — функциональную и статистическую (корреляционную).

17

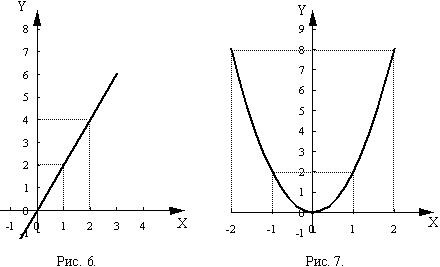
Будем говорить, что между двумя признаками X и Y существует функциональная зависимость (взаимосвязь), при которой каждому значению одного из них соответствует одно или несколько строго определенных значений другого.

Например, в функции у = 2*х каждому значению х соответствует в два раза большее значение у. В функции каждому значению у соответствует 2 определенных значения х. Графически это выглядит так (рис. 6, 7 соответственно):

Будем говорить, что между двумя признаками Х и У существует корреляционная зависимость (взаимосвязь), при которой с изменением одного признака изменяется и другой, но каждому значению признака Х могут соответствовать разные, заранее непредсказуемые значения признака У, и наоборот.

Для различия направленности влияния одного признака на другой введены понятия положительной и отрицательной связи.

Если с увеличением (уменьшением) одного признака в основном увеличиваются (уменьшаются) значения другого, то такая корреляционная связь называется прямой или положительной.

Если с увеличением (уменьшением) одного признака в основном уменьшаются (увеличиваются) значения другого, то такая корреляционная связь называется обратной или отрицательной.

3.2. Корреляционные поля и их использование в предварительном анализе корреляционной связи

При постановке вопроса о корреляционной зависимости между двумя статистическими признаками Х и У проводят эксперимент с параллельной регистрацией их значений.

Пример 1. Определить, зависит ли результат прыжка в длину с разбега (признак Х) от величины конечной скорости разбега (признак У). Для ответа на этот вопрос параллельно с регистрацией результата Х каждого прыжка спортсмена или группы спортсменов регистрируют и величину конечной скорости разбега Y . Пусть они таковы:

18

Рис. 8. График корреляционного поля.

Будем называть корреляционным полем зону разброса таким образом полученных точек на графике. Визуально анализируя корреляционное поле на рисунке 8, можно заметить, что оно как бы вытянуто вдоль какой-либо прямой линии. Такая картина характерна для так называемой линейной корреляционной взаимосвязи между признаками. При этом можно в общем предположить, что с увеличением конечной скорости разбега увеличивается и длина прыжка, и наоборот. Т.е. между рассматриваемыми признаками наблюдается прямая (положительная) взаимосвязь.

Наряду с этим примером из множества других возможных корреляционных полей можно выделить следующие (рис.9-11):

19