Автоматизированный лабораторный комплекс ТМл-18 «Двойной маятник» (96

1. НАЗНАЧЕНИЕ И СОСТАВ ЛАБОРАТОРНОГО КОМПЛЕКСА

Автоматизированный лабораторный комплекс ТМл-18 предназначен для экспериментального и теоретического исследования колебаний парциальных систем и главных колебаний двойного маятника. Лабораторный комплекс позволяет экспериментально определить основные параметры колебательной системы, а затем, построив математическую модель, сравнить результаты экспериментального исследования главных колебаний системы с данными, полученными при математическом моделировании.

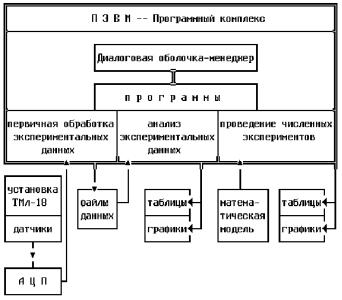
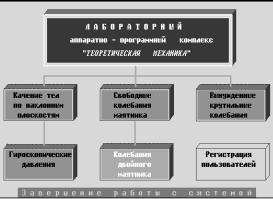
Автоматизированный лабораторный комплекс ТМл-18 состоит из прибора ТМл-18, аналого-цифрового преобразователя (АЦП), ПЭВМ типа IBM PC и программного комплекса. Программаменеджер обеспечивает согласованное взаимодействие всех компонентов лабораторного комплекса (рис. 1).

Рис. 1. Блок-схема лабораторного комплекса

3

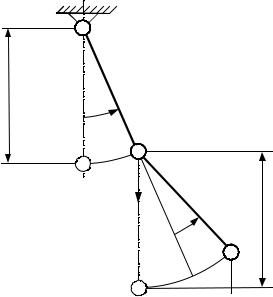
В модели двойного маятника (рис. 2) однородный стержень О1А прикреплен к неподвижному основанию с помощью шарнирного узла О1, имеющего горизонтальную ось. На нижнем конце стержня О1А закреплен шарнирный узел О2, имеющий ось, параллельную оси шарнирного узла О1. К нижнему концу стержня O2B прикреплен груз В. В шарнирных узлах О1 и О2 расположены датчики, фиксирующие углы отклонения стержней О1А и О2В – α1 и α2 соответственно.

O1

P2

Рис. 2. Модель двойного маятника

Угол α1 является абсолютным углом отклонения стержня О1А от вертикали, а угол α2 – относительный угол, т. е. угол поворота стержня О2В вокруг оси шарнира О2 относительно стержня О1А.

В качестве чувствительного элемента в датчиках применены потенциометры, которые питаются от АЦП постоянным напряжением ±5 В.

4

2. СОСТАВЛЕНИЕ СИСТЕМЫ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ ДВИЖЕНИЯ

Чтобы записать дифференциальные уравнения движения, сначала необходимо принять физическую модель системы (см. рис. 2). В качестве такой модели выберем систему твердых тел, соединенных между собой цилиндрическим шарниром О2. Будем считать, что стержни О1А и О2В имеют длины l1 и l2 соответственно и являются невесомыми, а шарнирный узел О2 и груз В – точечные массы, m1 и m2. Трением в шарнирах О1 и О2 и сопротивлением воздуха пренебрегаем. На рис. 2 показаны силы тяжести P1 и P2, равные m1g и m2g соответственно (g – ускорение свободного падения).

Для составления дифференциальных уравнений движения механической системы воспользуемся уравнениями Лагранжа второго рода.

Полагая углы α1 и α2 малыми, выражения для кинетической T и потенциальной П энергий системы можно записать следующим образом:

С учетом принятых обозначений дифференциальные уравнения движения можно представить так:

Сложность аналитического решения системы дифференциальных уравнений (3) обусловлена тем, что прибор ТМл-18 является неразборным, и поэтому нельзя измерить значения масс m1 и m2, которыми определяются значения коэффициента γ.

5

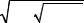
Коэффициент n определяет вторую (высшую) парциальную частоту системы – n2. Значение этой частоты можно найти экспериментально, закрепив стержень О1А. Значение первой (низшей) парциальной частоты n1 также можно определить экспериментально. Для этого достаточно исследовать колебания системы, в которой оба стержня жестко скреплены между собой, т. е. расчетную схему для этого случая можно представить в виде невесомого стержня О1В, на котором закреплены точечные грузы А и В. Таким образом, имеется возможность измерить длины l1 и l2 и экспериментально определить значения частот n1 и n2.

Введем еще один коэффициент, учитывающий отношение парциальных частот, – θ = (n1/n2)2.

Тогда коэффициент γ можно определить как

Итак, имеется возможность экспериментально-аналитическим способом определить коэффициенты системы дифференциальных уравнений:

Учитывая введенные обозначения, собственные частоты ω1 и ω2 системы можно определить по формуле

6

Общее решение системы дифференциальных уравнений (3):

3. ПРОВЕДЕНИЕ ЭКСПЕРИМЕНТА И ОБРАБОТКА ПОЛУЧЕННЫХ РЕЗУЛЬТАТОВ

3.1.Включение и запуск комплекса

Спомощью кабеля, входящего в комплект установки ТМл-18, следует подключить датчики углов поворота стержней маятника к АЦП, размещенному в компьютере. При этом компьютер должен быть выключен из сети.

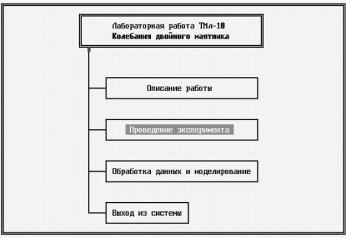
Затем надо включить компьютер и запустить файл astart.bat. На экране появится главное меню компьютерной системы (рис. 3).

Вглавном меню следует войти в раздел «Колебания двойного маятника».

Рис. 3. Главное меню компьютерной системы

7

Эксперимент должен проводиться в два этапа. На первом этапе нужно будет зафиксировать колебания двух парциальных систем – каждой по отдельности. После этого по полученным графикам парциальных колебаний системы требуется рассчитать парциальные частоты, измерить длины маятников и перейти ко второму этапу – исследованию главных колебаний.

3.2. Исследование парциальных систем

Исследование первой парциальной системы

Результатом экспериментального исследования должна быть частота колебаний первой парциальной системы.

Рис. 4. Подменю лабораторной работы

В подменю лабораторной работы следует войти в раздел «Проведение эксперимента» (рис. 4). При этом запустится программа, обеспечивающая проведение физического эксперимента. После запуска программы необходимо:

а) ввести имя файла, в котором будут размещены данные, полученные экспериментально;

б) задать временной интервал между измерениями угла поворота стержня маятника и ввести интервал времени проведения эксперимента;

8

в) протарировать датчики углов поворота маятников. Для этого следует груз А установить на верхний левый фиксатор, а груз В – на нижний правый фиксатор и зафиксировать это положение. Затем надо вернуть стержни в вертикальное положение и также зафиксировать это положение;

г) после проведения тарировки необходимо скрепить между собой стрежни О1А и О2В с помощью специального приспособления, входящего в комплект поставки установки;

д) установить груз А на левый верхний фиксатор, при этом оба стержня окажутся повернутыми на одинаковый угол;

е) нажать на клавиатуре клавишу «Пробел» и отключить фиксатор – данные, снимаемые с датчиков, будут записаны в файле под указанным вами именем; после окончания записи колебаний первой парциальной системы программа вернется к пункту меню «Проведение эксперимента» (см. рис. 4);

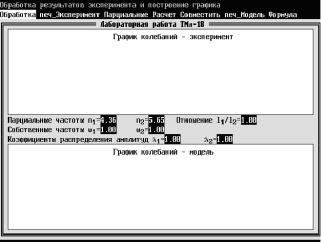
ж) обработать полученные данные. Для этого в подменю лабораторной работы необходимо войти в раздел «Обработка данных и моделирование». Диалоговая панель этого раздела имеет два окна для вывода графиков колебаний реального маятника и математической модели (рис. 5);

Рис. 5. Диалоговая панель парциальных систем

з) в меню этого раздела выбрать пункт «Обработка». При запуске этого режима система запросит имя файла с эксперимен-

9

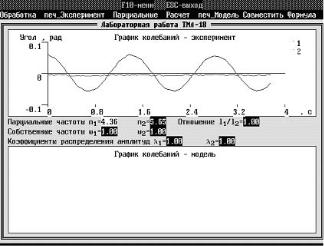
тальными данными, начальное значение угла отклонения и значение временного интервала записи колебаний маятника (значение этого интервала может быть и меньше интервала записи). После ввода этих данных запустится процедура обработки экспериментальных данных и построения графика, который будет выведен в верхнем окне панели. Полученный график следует распечатать, выбрав пункт меню «печ_Эксперимент» (рис. 6).

Рис. 6. Колебания первой парциальной системы. Экспериментальные кривые

Распечатанный график подлежит обработке для получения первой парциальной частоты.

Исследование второй парциальной системы

Результатом экспериментального исследования должна быть частота колебаний второй парциальной системы.

В подменю лабораторной работы следует войти в раздел «Проведение эксперимента» (см. рис. 4). При этом запустится программа, обеспечивающая проведение физического эксперимента. После запуска программы необходимо:

а) ввести имя файла, в котором будут размещены данные, полученные экспериментально;

б) задать временной интервал между измерениями угла поворота стержня маятника и ввести интервал времени проведения эксперимента;

10