Методы оптимальных решений. Методические указания и контрольные задания для студентов-заочников экономических специальностей (110

Ресурсы поставщиков записывают в столбце аi, потребности потреби-

телей – в строке bj, тарифы – в левом верхнем углу соответствующих клеток таблицы;

2). Составляется опорный план. Наиболее эффективным методом для его получения является метод наилучших оценок. Самые низкие тарифы,

равные 1, в клетках (1,1) и (3,2), то есть наиболее выгодные (самыми деше-

выми) являются поставки груза от поставщика А1 к потребителю В1 и от А3 к

В2. С этих клеток начинается планирование грузоперевозок. Итак, потребите-

лю В1 необходимо 35 ед. груза. Поставщик А1, наиболее эффективный для этого потребителя, может удовлетворить его потребности полностью. Поэто-

му в клетку (1,1) записывается величина поставки 35. Для потребителя В2

наиболее эффективный поставщик А3 может обеспечить лишь часть его по-

требности в грузе. Поэтому в клетку (3,2) записывается величина поставки

15, составляющая весь ресурс А3. Недостающие 45 ед. груза обеспечи-

11

вает поставщик А2, являющийся наиболее эффективным после А3 поставщи-

ком груза для В2. Наконец, для потребителя В3 наиболее эффективным явля-

ется поставщик А2, оставшийся ресурс которого позволяет обеспечить 20 ед.

груза для В3. Недостающие 20 ед. груза можно взять только у А1.

ные транспортные расходы (величина целевой функции задачи) в данном случае будут равны

C0 = 1∙35 + 6∙20 + 2∙45 + 3∙20 + 1∙15 = 320;

3). Полученный план проверяется на невырожденность. Невырожден-

ным считается вариант плана, в котором количество заполненных клеток l =

m = 3, n = 3, l = 5 = m + n – 1. Следовательно, данный вариант плана являет-

ся невырожденным.

Необходимо заметить, что в случае l< m + n – 1 невырожденности пла-

на добиваются, заполнением недостающих клеток нулями, причём целесооб-

разно выбирать клетки с меньшими тарифами.

4). План проверяется на оптимальность. С этой целью вводят потенци-

алы строк Ui и потенциалы столбцов Vj. Индексы i или j потенциалов озна-

чают номера соответствующих поставщиков или потребителей.

Для всех заполненных клеток должно выполняться условие

Ui + Vj = Сij.

Для рассматриваемого плана получаем систему уравнений:

Эта система линейных уравнений неопределенна, поскольку для нахождения 6 потенциалов имеется только 5 уравнений. Чтобы получить ка-

кое-либо её решение, один из потенциалов полагают равным произвольному числу. Пусть для определенности U1 = 0. Тогда остальные 6 неизвестных по-

тенциалов однозначно определяются из системы уравнений:

U2 = - 3, U3 = - 4, V1 = 1, V2 = 5, V3 = 6.

Полученные значения потенциалов записывает в соответствующие клетки транспортной таблицы:

Для рассматриваемого плана получаются следующие оценки незапол-

ненных клеток:

∆(1,2) = 3 - (0 + 5) = -2,

∆(2,1) = 4 - (-3 + I) = 6,

∆(3,1) = 2 - (-4 + I) = 5.

∆(3,3) = 5 - (-4 + 6) = 3.

При оптимальном плане для всех незаполненных клеток их оценки не-

отрицательные.

В нашем случае полученный план перевозки грузов Хо не является оп-

тимальным и может быть улучшен путем перераспределения части груза в

13

клетку (1,2), имеющую отрицательную оценку, где нарушается условие оп-

тимальности.

Примечание: если при проверке плана на оптимальность оказывается,

что несколько незаполненных клеток имеют отрицательные оценки, то груз перераспределяют в клетку с наиболее отрицательной оценкой. Если же наиболее отрицательная оценка получается у двух или более клеток, то груз перераспределяют в клетку с наименьшим среди них тарифом;

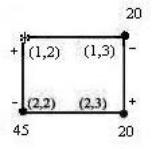
5). Составляется новый вариант плана. С этой целью для клетки (1,2), в

которой не выполняется признак оптимальности, строится «замкнутый маршрут», который представляет собой замкнутый многоугольник с прямы-

ми углами, все вершины которого расположены в заполненных клетках, кро-

ме одной – (1,2).

Вершину полученного многоугольника,

расположенную в клетке нарушения опти-

мальности (1,2), обозначают знаком (+), сле-

дующую (-) и далее знаки чередуются. Затем из вершин, обозначенных знаком (-), выбирается наименьшая величина поставки (в данном случае min {20;45} = 20) и она

прибавляется к запланированному объему грузоперевозки в клетках, где вершины обозначены знаком (+), и вычитается из запланированного объема грузоперевозки в клетках, где вершины обозначены знаком (-). В результате

Суммарные транспортные расходы (величина целевой функции) при таком плане составляют

C1 = 1∙35 + 3∙20 + 2∙25 + 1∙15 + 3∙40 = 280.

При этом С1 <C0.

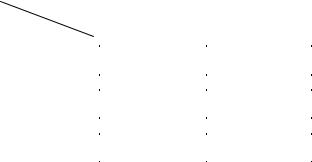
Результаты запишем в новую транспортную таблицу:

14

Далее алгоритм метода потенциалов повторяется. Полученный план проверяется сначала на невырожденность, а затем – на оптимальность. В

этом случае имеем:

Отсюда, полагая V2 = 0, получаем: U1 = 3, U2 = 2, U3 = 1, V1 = -2, V3 = 1.

Оценки незаполненных клеток согласно (3,2) будут таковы:

∆(1,3) = 6 - (3 + 1) = 2,

∆(2,1) = 4 - (2 - 2) = 4,

∆(3,1) = 2 - (1 - 2) = 3,

∆(3,3) = 5 - (1 + 1) = 3.

Поскольку все оценки неотрицательные, заключаем, что найденный

нами план является оптимальным.

15

2. ТЕОРИЯ ИГР

Программные вопросы

1.Математическое моделирование и его основные этапы.

2.Понятие конфликта. Предмет теории игр.

3.Понятие конечной игры. Матричная игра и платёжная матрица. За-

дание матричной игры платёжной матрицей.

4.Принцип максимина для матричных игр. Седловая точка матричной игры. Понятие решения и цены игры.

5.Смешанное расширение матричной игры. Основная теорема теории матричных игр.

6.Методы решения матричных игр: прямое (непосредственное) реше-

ние; графо-аналитический метод; решение матричных игр методами линей-

ного программирования.

7. Понятие игры с природой. Критерии оптимальности Вальда,

Гурвица, Лапласа и Сэвиджа для игр с природой.

Литература.

1. Уейская, Н.Б. Теоретико-игровые модели в экономике: Учебное по-

собие для студентов экономического факультета / Н.Б. Уейская Саратов: Са-

рат. с.-х. акад. 1996, 96с.

2. Уейская Н.Б. Задачи и упражнения по теории игр для экономистов: учеб. по-

собие /Н.Б. Уейская. - Изд. ФГБОУ ВПО СГАУ. Саратов, 2012. 55 с.

3. Розен В.В. Модели принятия решений в экономике. Учебное посо-

бие./ В.В. Розен М: Книжный дом «Университет», Высшая школа, 2002. 288с.

Решение типового примера задания №4

Фирма может выставить на рынок три вида товара. В зависимости от

16

состояния рынка её доходы в денежных единицах представлены в таблице:

Требуется составить модель матричной игры и найти

а) нижнюю цену игры и все максиминные стратегии игрока 1;

б) верхнюю цену игры и все минимаксные стратегии игрок2;

в) цену игры и седловые точки, если они существуют;

г) рассматривая её как игру с природой, найти оптимальные стратегии игрока 1 по критериям Вальда, Гурвица, полагая коэффициент пессимизма

= 0,2 и =0,5, Сэвиджа и Лапласа.

Решение. Составим модель матричной игры.

Множество игроков I={1, 2}, где 1 – фирма, 2 – рынок. Множество стратегий (возможных действий) игрока 1 обозначим S1 {1,2,3}, элементы которого есть виды товаров. Для игрока 2 его множество стратегий S2 {1,2,3,4}, элементы которого представляют собой состояния рынка, а

матрица игры, элементы которой равны доходам в денежных единицах игро-

ка 1 в во всевозможных ситуациях (определяются парой стратегий выбран-

среда ведёт себя наихудшим образом по отношению к принимающему реше-

ние, то игру можно рассматривать как матричную.

а). Для нахождения нижней цены игры и максиминных стратегий игро-

ка 1 в каждой строке платёжной матрицы выбираем минимальный элемент

(наименьший возможный выигрыш игрока 1 при применении соответствую-

щей стратегии) и выписываем его в отдельный столбец. Затем выбираем в

17

построенном столбце максимальный элемент или элементы, если их окажет-

ся несколько, и отметим их звёздочкой. Он (они) и будут равны нижней цене игры, а номера строк, в которых расположены эти элементы будут соответ-

ствовать максиминным стратегиям игрока 1. В нашем случае имеем: minaij

j

Таким образом, нижняя цена игры v =1, а максиминная стратегия иг-

рока 1: i* 2.

б). Для нахождения верхней цены игры и минимаксных стратегий иг-

рока 2 находим в каждом столбце платёжной матрицы максимальный эле-

мент (наибольший возможный проигрыш игрока 2 при применении соответ-

ствующей стратегии) и выписываем его в отдельную строку, а затем выбира-

ем в построенной строке минимальный элемент или элементы, если их ока-

жется несколько, и также отметим их звёздочкой. Он (они) и будут равны верхней цене игры, а номера столбцов, в которых расположены эти элементы будут соответствовать минимаксным стратегиям игрока 2.

Таким образом, верхняя цена игры v =1. Минимаксная стратегия игрока

2 : j* 2.

в). Седловая точкаэто ситуация выигрыш первого игрока в которой есть элемент, являющийся одновременно самым маленьким в своей строке и

самым большим в своём столбце. Такая ситуация существует, если

18

v = v = v и образуется любой парой соответственно максиминной и мини-

максной стратегий, при этом v называют ценой игры, а седловую точку её решением, так как ни одному из игроков невыгодно отклониться от неё в од-

ностороннем порядке.

В нашем случае v=1. Седловая точка (2, 2).

г). Поскольку игрок 2 – рынок (стихийная сила), то игру можно рас-

сматривать как игру с природой.

Оценим стратегии игрока 1, используя Критерий Вальда, основаный на гипотезе крайнего пессимизма игрока по отношению к поведению среды,

а именно: предполагается, что среда ведёт себя наихудшим образом по от-

ношению к принимающему решение.

Оптимальной по данному критерию стратегией является максиминная стратегия. В нашем случае это стратегия 2.

Критерий Гурвица связан с введением так называемого коэффициента

пессимизма α ( 0 1). Гипотеза о поведении среды состоит в том, что

наихудший вариант реализуется с вероятностью α, а наилучший с вероятно-

стью 1-α.

Оптимальной по этому критерию считается та стратегия, для которой

Оценим стратегии игрока при α=0,2 и 1- α=0,8:

Для стратегии 1: 0,2 ( 2) 0,8 2 1,2

Для стратегии 2: 0,2 1 0,8 3 2,6

Для стратегии 3: 0,2 ( 3) 0,8 4 2,6 .

Оптимальные стратегии: 2 и 3.

19

Аналогично, оценим стратегии игрока при α=0,5и 1- α=0,5:

Оптимальная стратегия: 2.

Критерий Лапласа основан на гипотезе равной вероятности состояний

среды. Оптимальной по этому критерию является та стратегия, для которой среднее арифметическое возможных выигрышей будет наибольшим.

Для стратегии 1:

Для стратегии 2:

Для стратегии 3:

Оптимальная стратегия: 2.

Критерий Сэвиджа основан на преобразовании матрицы выигрышей

Оптимальная стратегия: 2.

Ответ: а) v =1; максиминная стратегия: 2; б) v =1; минимаксная стра-

тегия: 2; в) цена игры 1; седловая точка (2,2); г) оптимальная по критерию Вальда стратегия 2, выигрыш 1; оптимальные стратегии по критерию Гурви-

ца ( = 0,2) 2 и 3, выигрыш 2,6; ( =0,5) стратегия 2 выигрыш 2;

20