
Методы обработки и планирования эксперимента. Ч.1. Оценка распределений и их параметров (110
.pdf
Параметры группировки гистограммы на рис. 1.3.
a := −3.15 |
b := 3.15 |
|
||||
R := 9 |
dx := |
(b − a) |
|
dx = 0.7 |
||
R |
||||||
|
|
|
||||
xT = (−2.8 −2.1 |
−1.4 |
−0.7 0 0.7 1.4 |
2.1 2.8 ) = xj . |
|||
В данном случае выборочное среднее и выборочная дисперсия определяются следующим образом:
M
XG = p j x j;
j=1
|
|
M |
|
|
2 |
|
M |
|
|
2 |
|
2 |
|
|
|
|
|||||||
p j (x j ) |
− |
p j x j |
|
||||||||
SG = |
|
|
. |
||||||||
|
j=1 |
|
|
j=1 |
|
|
|
|
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
Выборочные начальные моменты по сгруппированным данным:
M |
(k =1,4). |
mG,k = p j (x j )k , |
j=1
(1.17)
(1.18)
Необходимо отметить, что группировка данных приводит к методическим ошибкам определения моментов распределения, которые можно уст-
ранить с помощью поправок Шеппарда:
|
|
|
|
|
|
|
= m (X ) − h2 ; |
|
|||||
X |
G |
= X; m |
|
|
|||||||||
|
|
|
|
|
G,2 |
2 |
|
12 |
(1.19) |
||||
|
|
|
|
|
|
|
|
|
Xh2 |
|
|||
m |
|
|
= m (X ) − |
|
|
|
|||||||
|
G,3 |
3 |
|
4 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
m (X )h2 |
|
7h4 |
|
|||
mG,4 = m4(X ) − |
2 |
|
|
+ |
|
; |
|||||||
|
2 |
|
240 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
Здесь моменты с индексом G относятся к группированным выборкам (1.17)−(1.20), а mk (X ) – выборочные моменты k-го порядка по негруппиро-
ванным выборкам (1.2).
Данные поправки могут быть применены при следующих распределе-
ниях: гауссовском, Рэлея, Максвелла, Симпсона; неприменимы при равномерном, экспоненциальном и др.
11

Пример расчета моментов с поправкой Шеппарда
|
|
n := 1000 |
|
|
|
|
|
|
|
|
Построение гистограммы |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
X := rnorm ( n , 0 , 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a := min(X) |
|
b := max ( X) |
|
|
|
|
a = − 3.376 b = 3.253 |
|||||||||||||||
a := − 3.25 |
b := 3.25 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
R := 5 |
dx := |
(b − a) |
|
|
|
|
|
|
dx = 1.3 |
|
|
|||||||||||
|
|
R |
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
j := 0 .. R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
intj := a + |
j dx |
q |
:= hist( int , X) |
|
|
|
p := |
q |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||
k := |
0 .. R − 1 |
|
|
xk := |
intk + 0.5 dx |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0.42 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
p k |
0.33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
0.25 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
0.17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0.083 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
2 |
|
|
1 |
|
0 |
|
1 |
2 |
3 |
|||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x k |
|
|
|
|
|
|
|||
mean (X) = 0.041 |
|
|
|
|
|
|
|
|
|
|
|
|
R− 1 |
|||||||||
|
|
|
|
|
|
|
|
MG := |
pk xk |
|||||||||||||
MG = 0.046 |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 0 |
|||||||||
|
|
|
|
n− 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
R− 1 |
||||
S2 := |
n1 |
(Xi)2 |
|
|
|
|
|
SG2 := |
pk (xk)2 |
|||||||||||||
|
|
|
|
i = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
k = 0 |
||||
S2 = 1.048 |
|
|
|
|
|
|
|
|
|
|
|
|
SG2 |
= 1.181 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
SG2 − S2 = 0.133 |
|
|
|
|
|
SH := |
SG2 − |
dx2 |
|
|
|
|
||||||||||
|
|
|
|
|
12 |
|
|
|
|
|||||||||||||
SH = 1.04 |
|
|
|
|
S2 − SH |
|
= 7.357 × 10 − 3 |
|||||||||||||||
12

2. ОЦЕНКИ ПРИ ИЗВЕСТНОМ (С ТОЧНОСТЬЮ ДО ПАРАМЕТРОВ) РАСПРЕДЕЛЕНИИ ВЫБОРКИ
Оценки по методу моментов
Если теоретическое распределение Fξ (x,θ ) известно с точностью до l параметров θ = {θ1, ...θl } , то решается система уравнений
Mg j (θ ) = g j (x)dFξ (x,θ ) = |
1 g j (Xi ) , j = 1... l . |
(2.1) |
|
n |
|
n i=1
Здесь g j (x) – некоторые функции выборки, j = 1... l . Выбор функций определяется удобством решения системы уравнений.
Оценки максимального правдоподобия (ОМП)
На основе выборки формируется функция правдоподобия
n
Λ(θ1, ..., θl ) = Wξ (x1, ..., xn |θ ) = ∏Wξ (xi |θ ) .
|
|
|
|
|
|
|
|
|
i=1 |
|
Далее решается система уравнений правдоподобия |
|
|||||||||
|
∂Λ(θ |
, ..., θ |
) |
|
∂ ln (Λ(θ1 |
, ..., θl )) |
|
|
|
|
|
1 |
l |
|
= |
|
|
= 0 |
, |
j = 1..l . |
(2.2) |
∂θ j |
|
|
|
|||||||
|
|
|
∂θ j |
|
|
|
||||
Кроме функции ln(x) может быть использована любая монотонная
функция.
Пример. Найти оценки параметров гамма – распределения
|
|
w(x) = |
λ c xc−1 exp(−λ x), x |
≥ 0, c,λ > 0 . |
(2.3) |
||||||||
|
|
|
|
Γ(c) |
|
|
|
|
|
|
|
|
|
по методу моментов и ОМП. |
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение по методу моментов |
|
||||||||||
математическое ожидание |
и |
дисперсия |
гамма-распределения |
равны |
|||||||||
m = c / λ, D = c / λ 2 . |
|
|
|
|
|
|
|
|
|
|
|||
Система уравнений (2.1) имеет вид |
|
|
|
|
|
|
|||||||
c / λ = X = 1 xi , c / λ 2 |
= S 2 = |
|
1 (xi − X )2 . |
|
|||||||||
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
n i=1 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
n −1 |
i=1 |
|
|
|
|
||||
Тогда оценки параметров плотности (2.3) |
|
|
|
|
|||||||||
|
|
|
|
|
c = (X |
)2 |
S 2 . |
|
|
|
(2.4) |
||
|
|
λ = X |
S 2 , |
|
|
|
|||||||
ОМП |
|
|
|
|
|
|
|
|
|
|
|||
Функция правдоподобия имеет вид
13

|
|
|
|
nc |
n |
c−1 |
|
|
|
n |
λ c xc−1 |
|
λ |
|
∏ xi |
|
n |
|
|
Λ(c,λ ) = ∏ |
i |
exp(−λ xi ) = |
|
|
i=1 |
|
exp |
−λ xi . |
|
|
(Γ(c)) |
n |
|||||||
i=1 |
Γ(c) |
|
|
|
|
i=1 |
|
||
Тогда уравнения правдоподобия (2.2) записываются в виде
n |
|
|
|
∂ ln (Λ(c,λ ) / ∂λ = (nc / λ ) − xi = 0 |
. |
(2.5) |
|
i=1 |
|||
|
|
n
∂ ln (Λ(c,λ ) / ∂c = nln(λ ) + ln(xi ) − nψ (c) = 0
i=1
Здесь ψ (c) = d (ln (Γ(c))) / dc -пси функция. Как видим, ОМП может при-
водить к системе нелинейных уравнений. Оценки (2.4) реализуются проще,
чем (2.5)
Задача: Найти параметр распределения Пуассона.
Метод моментов (пример неоднозначности метода моментов) Выборка X = ( X1, X2 , ..., Xn )
пределением
P(k,λ ) = |
λ k exp(−λ ) |
. |
(2.6) |
|
|||
|
k! |
|
|
Первые моменты случайной величины ξ , образующей генеральную
совокупность выборочных значений
m =< ξ >= λ
D(ξ ) =< (ξ − m)2 >= λ.
Потому возможны, по крайней мере, два уравнения
|
|
|
|
n |
|
||
• |
λ = X |
= Xi / n |
(2.7) |
||||
|
|
|
|
i=1 |
|
||
|
|
1 |
|
n |
|
||
• |
λ = SX2 = |
|
(X i − X |
)2 . |
(2.8) |
||
|
|
|
|||||
|
|
n −1 i=1 |
|
||||
Вообще говоря, у закона Пуассона первые 4 кумулянта равны λ . Поэтому возможны и другие решения по методу моментов.
ОМП (Пример однозначности)
Для формирования функции правдоподобия подставляем в (2.6) k = Xi , i = 1..n . Тогда функция правдоподобия имеет вид
|
|
|
n |
|
|
λ Xi exp(−λ ) |
|
Xi |
|
n |
|
λ i=1 |
|
|
Λ(λ ) = ∏ |
|
= |
|
exp(−λn) . |
( Xi )! |
n |
|||
i=1 |
|
∏ ( Xi !) |
|
|
|
|
|
i=1 |
|
Соответственно,
n
ln[Λ(λ )] = −λn + ln(λ ) Xi + c(X ) ,
i=1
14

|
d ln[Λ(λ )] = −n + |
1 Xi . |
|
||||
|
|
|
|
|
|
n |
|
|
dλ |
|
|
|
λ |
i=1 |
|
Следовательно, оптимальная оценка параметра λ |
|
||||||
|
|
|
|
n |
|
|
|
|
|
λ = X |
= |
1 Xi . |
(2.9) |
||
|
|
|
|
n i=1 |
|
|
|
Сравнение (2.7)−(2.9) показывает однозначный вид оценки при ОМП.
Обработка неравноточных измерений
Пусть имеется выборка X = ( X1, X2 , ..., Xn ) , где Xi N (m,σ i2 ).
То есть все измерения имеют разную дисперсию. Запишем функцию правдоподобия относительно параметра m
n
Λ(m) = ∏
i=1
1 |
|
|
(Xi − m)2 |
|
|
|
exp |
− |
2 |
. |
(2.10) |
|
|||||
2πσ i2 |
|
|
2σ i |
|
|
Обозначим gi = 1/ σ i2 . Тогда
n
ln (Λ(m)) = gi (Xi − m)2 / 2 + B ,
i=1
где В, слагаемое, не зависящее от ( Xi ,m) . Решаем уравнение
|
d ln (Λ(m)) = gi ( Xi − m) = 0 . |
||||||||
|
|
|
|
|
|
n |
|
|
|
|
dm |
|
|
|
|
i=1 |
|
|
|
Получаем оценку ОМП |
|
|
|
|
|
|
|
||
m = |
n |
|
Xi |
n |
|
|
|||
gi |
gi . |
|
(2.11) |
||||||
|
|
|
i=1 |
|
|
i=1 |
|
|
|
Оценка ОМП является несмещенной |
|
|
|
|
|||||
|
|
|
|
n |
|
|
|
n |
|
|
< m >= |
gi < Xi > |
m gi |
= m . |
|||||
|
i=1 |
n |
= |
n |
|||||
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
gi |
|
|
gi |
|
|
|
|
|
|
i=1 |
|
|
i=1 |
|
Дисперсия оценки
D(m)
n
gi2 D(Xi )
= |
i=1 |
|
|
|
|
n |
2 |
|
|
gi |
|
|
|
i=1 |
|
=n 1 .
gi
i=1
Пусть Xn – самое точное измерение с дисперсией D(Xn ) = σ n2 = 1/ gn . Поскольку gi > 0 , то ОМП точнее самого точного измерения. Посколь-
ку gi > 0 , то ОМП точнее самого точного измерения
Объединение оценок
Пусть имеются две серии равноточных измерений из k и n измерений
15
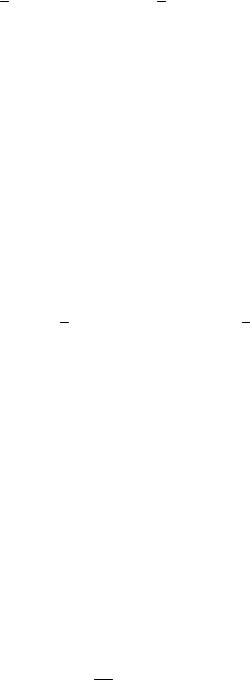
X |
(1) |
= (X1(1) , X2(1) ..., Xk(1) ) |
Xi(1,2) |
N (m,σ 2 ) . |
(2.12) |
|
|
(2) |
= (X1(2) , X2(2) |
..., Xn(2) ) |
|||
X |
|
|
|
|||
По этим сериям вычислены выборочные средние значения
|
|
|
k |
|
|
|
n |
|
|
|
= (1/ k) Xi(1) , |
|
|
|
= (1/ n) Xi(2) . |
X |
(1) |
X (2) |
|||||
|
|
|
i=1 |
|
|
|
i=1 |
Применим обработку неравноточных данных к этим двум оценкам для их объединения
D(X |
(1) ) = |
σ 2 |
= |
1 |
, |
D(X |
(2) ) = |
σ 2 |
= |
1 |
. |
|
k |
g |
n |
|
|||||||||
|
|
|
|
|
|
|
g |
2 |
|
|||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
Тогда объединенная оценка среднего выборок (2.12)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
g X |
(1) |
+ g X (2) |
|
kX (1) |
+ nX (2) |
. |
(2.13) |
||||||||
X = |
= |
|||||||||||||||||
1 |
|
|
2 |
|
|
|
|
k + n |
||||||||||
|
|
|
|
|
g1 + g2 |
|
|
|
|
|
||||||||
Аналогично объединяются выборочные оценки дисперсии при известном математическом ожидании.
k (Xi(1) − m)2
S(1)2 = |
i=1 |
|
, |
|
k |
||
|
|
|
Отсюда
|
n |
|
|
S(2)2 = |
(Xi(2) − m)2 |
. |
|
i=1 |
|||
n |
|||
|
|
|
|
|
|
|
|
|
kS 2 |
+ nS 2 |
. |
|
|
|
|
|
|
SX2 |
= |
|
(1) |
(2) |
|
|
|
|
|||
|
|
|
|
|
|
|
k + n |
|
|
|
|
|
|
Если математические ожидания неизвестны, то |
|
|
|||||||||||
|
k |
|
|
|
|
|
|
|
n |
|
|
||
S(1)2 = |
(Xi(1) − X |
(1) )2 |
|
, |
S(2)2 = |
(Xi(2) − X |
(2) )2 |
. |
|||||
i=1 |
|
|
|
|
|
i=1 |
|
||||||
k −1 |
|
|
|
|
|
|
n −1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||
Весовые сомножители g1 = (k −1) / 2σ 4 , |
g2 = (n −1) / 2σ 4 . |
||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k |
−1)S 2 |
+ (n −1)S 2 |
|
|
||||||
|
SX2 = |
|
|
|
|
|
(1) |
|
(2) |
. |
|
|
|
|
|
|
|
|
|
k + n − 2 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||
Оценка математического ожидания и дисперсии при коррелированных отсчетах
Рассмотренные выше оценки получены в предположении, что отсчеты независимы. При коррелированности отсчетов выборки эти оценки резко
теряют свои оптимальные свойства. Пусть выборка X = x |
..., x |
T |
имеет га- |
|||
1, |
n |
|
|
|
|
|
|
|
|
|
|
T |
}. |
уссовское распределение с корреляционной матрицей K x = M {(X |
− m)(X |
− m) |
|
|||
Допустим, что все отсчеты xi (i = 1,n) имеют одинаковые математические
16

ожидания m и дисперсии σx2 (корреляционная матрица K x = σx2Rx , где R X – нормированная корреляционная матрица). Плотность вероятности вектора наблюдений X определяется следующим выражением:
|
|
1 |
|
|
T |
−1 |
|
|
/ |
(2π) |
n |
det( K x ) . |
(2.14) |
W (x) = exp − |
2 |
(x |
− m) |
|
K x |
(x |
− m) |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При фиксированной выборке X плотность вероятности (2.14) пред-
ставляет собой функцию правдоподобия. Решая уравнение правдоподобия, получаем следующие выражения:
|
n n |
|
|
n n |
c |
|
; |
S 2 |
|
n n |
(X |
|
− m) |
( |
X |
|
− m |
|
/ (n − 1) , |
m = |
c X |
|
/ |
|
|
= |
c |
i |
j |
|
|||||||||
|
ij |
j |
|
ij |
|
X |
ij |
|
|
|
|
) |
|
||||||
i=1 j=1 |
|
i=1 j=1 |
|
|
|
|
i=1 j=1 |
|
|
|
|
|
|
|
|
|
|||
где |
с – элемент (i, j) |
матрицы |
C= R−1 |
. Если измерения независимы, то |
||
|
ij |
|
|
|
x |
|
Rx |
– единичная матрица. Тогда |
ci, j = δi, j |
– символ Кронекера и получаем |
|||
|
|
|
|
|
n |
|
классическую оценку m |
|
|
= (1/ n) Xi . |
|
||
= X |
|
|||||
i=1
17
3. ВЫБОРОЧНЫЕ РАСПРЕДЕЛЕНИЯ И ИХ АНАЛИЗ
ОБЩИЕ СООТНОШЕНИЯ. Теоретическими вероятностными характеристиками для непрерывной случайной величины ξ являются:
−плотность вероятности Wξ (x) ;
−функция распределения Fξ (x) = P[ξ < x] = x Wξ (t )dt.
−∞
Для дискретной случайной величины ξ :
−Ρk = Ρ [ξ = xk ] – распределение вероятностей;
−Fξ (x) = Pk – функция распределения.
k:xk < x
При проведении эксперимента теоретическое распределение Fξ(x) может быть:
a)либо известно частично, с точностью до некоторых неизвестных параметров;
b)либо полностью неизвестным.
В первом случае экспериментальное определение Wξ (x), Fξ (x), Pk сво-
дится к оценке параметров распределения, которые находятся из выбо-
рочных моментов x, s2 , m2 .
Во втором случае производится непараметрическая оценка распределения на основе 1) эмпирической функции распределения, 2) гистограммы, 3) полигона накопленных частот. Эмпирической функцией распределения
называется оценка Fξ(x) по несгруппированной выборке. Гистограммой называется оценка плотности вероятности Wξ (x) по сгруппированным дан-
ным. Полигоном накопленных частот называется оценка функции распределения Fξ(x) по сгруппированным данным.
I. Правило построения эмпирической функции распределения |
|||
1. Берется выборка |
x |
= (x1, x2 , ..., xn ) объемом n > 100, производится ее |
|
упорядочивание x(1) ≤ x(2) |
... < x(n) . |
|
|
2. Строится функция |
|
1 n |
|
Fn (t, x) = |
U (t − x(i) ) , |
||
|
|
|
n i=1 |
где U(t) – функция Хевисайда.
18
1 |
1 |
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Fn(x, z) |
|
|
|
|
|
Fn(x, z) |
|
|
|
|
|
|
|
|
|
0.5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
cnorm(x) |
|
|
|
|
cnorm(x) |
0.5 |
|
|
|
|
|
|
|
|
0 |
0 4 |
2 |
0 |
2 |
4 |
0 |
0 |
4 |
|
2 |
0 |
2 |
4 |
|
|
|
|
|
|||||||||||
|
− 4 |
|
x |
|
4 |
|
|
− 4 |
|
|
x |
|
4 |
|
|
|
n = 1000 |
|
|
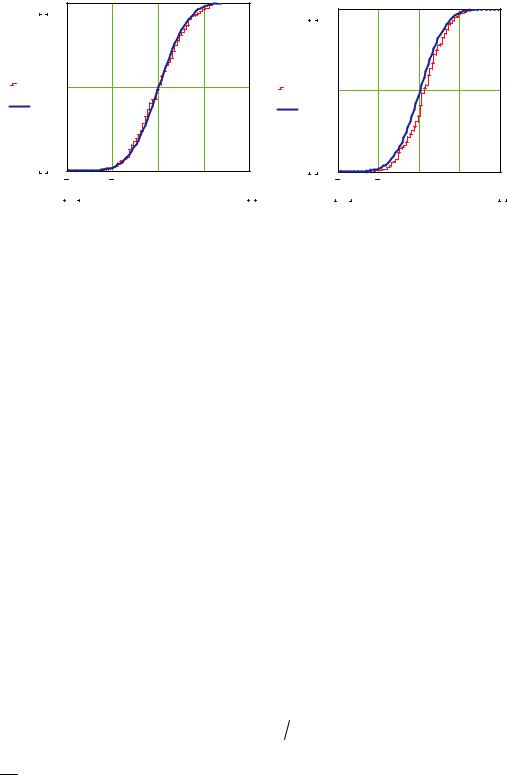
Рис. 3.1 |
|
|
|
|
n = 200 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
На рис. 3.1 приведены эмпирическая Fn (x) и теоретическая Fξ (x) |
функ- |
|||||||||||||
ции распределения при разных n. |
|
|
|
|
|
|
|
|
|
|
||||
II. Правило построения гистограмм: |
|
|
|
|
|
|
|
|
||||||
1. Берется |
выборка |
x |
= (x1, x2 ,..., xn ) |
объемом |
n |
> |
100, |
как |
правило, |
|||||
n ≈ (2 ÷ 20)102 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2. |
Определяется число интервалов группировки r: |
|
a) |
r = (0.55 ÷1.25)n0.4 ; |
b) r = (4 ÷ 5)lg n . |
Обычно число интервалов группировки 9 < r < 21. Если распределение предполагается симметричным, то r желательно брать нечетным.
3. Определяются длина и границы интервалов группировки. Для всех xi : a < xi < b , где
d = (b − a) = 1.02(xmax − xmin ), x = d / r = 1.02(xmax − xmin ) / r,
a = xmin − 0.01 x r, |
b = xmax + 0.01 |
x r. |
||
Границы j-го интервала j : |
j = (a + ( j −1) |
x;a + j x), j = |
|
. |
1, r |
||||
Для односторонних распределений (экспоненциального, релеевского, хи-квадрат и др.) левая граница интервала а = 0.
4. |
Подсчитывается количество kj элементов выборки x , попавших в |
||
интервал группировки |
j = (a + ( j −1) x;a + j |
x) . Число k j > 5 ÷10 . |
|
5. |
Определяются |
частоты ν j :ν j = k j n |
либо относительные частоты |
ω j :ω j = ν j  x = k j
x = k j  n x и строится диаграмма из столбцов высотой ν j или
n x и строится диаграмма из столбцов высотой ν j или
ω j , j = 1, r .
Гистограмма меньше всего отличается от теоретической в центре интервала группировки (a + ( j − 0.5) x) .
Пример. Пусть моделируется выборка с плотностью вероятности, приведенной на рис. 3.2.
19

|
1 |
|
|
|
−(x − m) |
2 |
|
−(x + m) |
2 |
f(x) := |
|
|
exp |
|
|
+ exp |
|
|
|
8 π |
|
|
|||||||
|
|
|
2 |
|
|
2 |
|
||
x := −4.5, −4.4.. 4.5 |
|
|
|
|
|
|
0.3 |
|
|
|
|
|
|
0.2 |
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
0.1 |
|
|
|
|
|
|
0 |
5 |
3 |
1 |
1 |
3 |
5 |
|
Рис. 3.2 |
|
x |
|
|
|
|
|
|
|
|
||
Гистограмма и теоретическая плотность вероятности приведены на рис. 3.3.
a := −5 |
b := 5 |
(b − a) |
|
|
||
r := 20 |
dx := |
|
|
|||
|
r |
|
|
|||
|
|
|
|
|
||
j := 0.. r − 1 |
intj := a + j dx |
N := hist(int, Y) |
last( N) = 18 |
|||
k := 0.. r − 2 |
ν k := |
|
Nk |
|
|
|
|
|
n |
|
|
||
|
|
|
|
|
||
0.15
0.1
ν k
f(x) dx
0.05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
4 |
|
|
|
|
2 |
0 |
|
|
|
2 |
4 |
|
6 |
|||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(k+ 0.5) dx+ a, x |
|
|
|
|
|
|
|
|
|
|
||||||||
Рис. 3.3
20
