|
Принцип Даламбера
|
|

Тонкий однородный
стержень длиной ℓ и массы
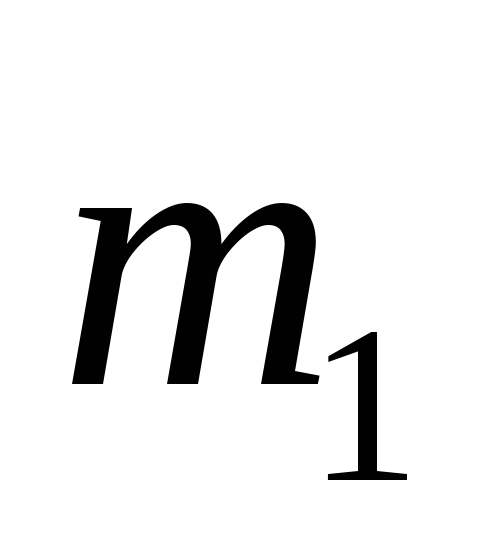 ,
на конце которого находиться точечный
груз массы ,
на конце которого находиться точечный
груз массы
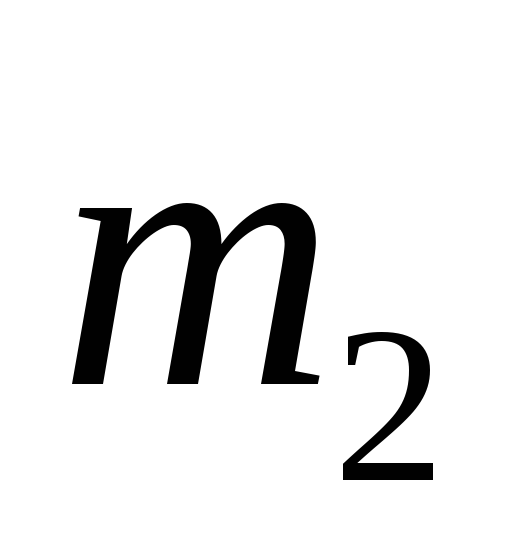 ,
может поворачиваться вокруг
горизонтальной оси О и вместе с
ней вокруг вертикальной оси СD.
Определить угловую скорость ω вращения,
если ,
может поворачиваться вокруг
горизонтальной оси О и вместе с
ней вокруг вертикальной оси СD.
Определить угловую скорость ω вращения,
если
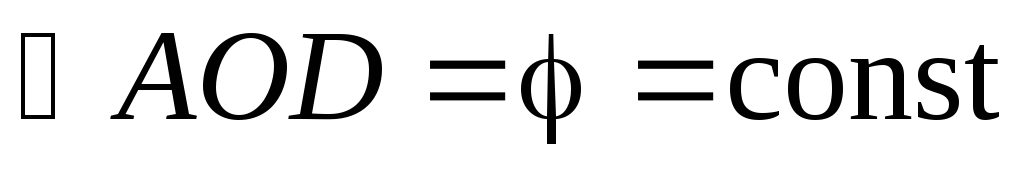 . .
|
|

Однородный стержень
АВ длиной ℓ и массой m
прикреплен шарниром А к вертикальному
валу, вращающемуся с постоянной угловой
скоростью ω. Определить величину T
натяжения нерастяжимой нити КВ
удерживающей стержень АВ под углом
α к вертикали.
|
|
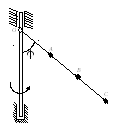
Стержень ОС
длиной 3l, на
котором закреплены 3 точечных груза
А, В, С равной массы m,
может поворачиваться вокруг
горизонтальной оси О и вместе с
ней вокруг вертикальной оси. Определить
угловую скорость
 установившегося вращения, если при
этом
установившегося вращения, если при
этом
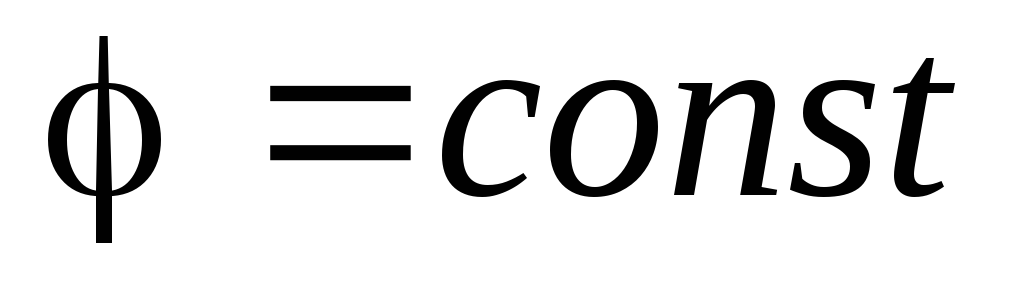 ,
ОА=АВ=ВС=l.
Массой стержня и трением можно
пренебречь. ,
ОА=АВ=ВС=l.
Массой стержня и трением можно
пренебречь.
|
|

На
рисунке показана схема регулятора,
состоящего из жесткого равнобокого
угольника АОВ ( ),
на концах которого находятся материальные
точки массой ),
на концах которого находятся материальные
точки массой
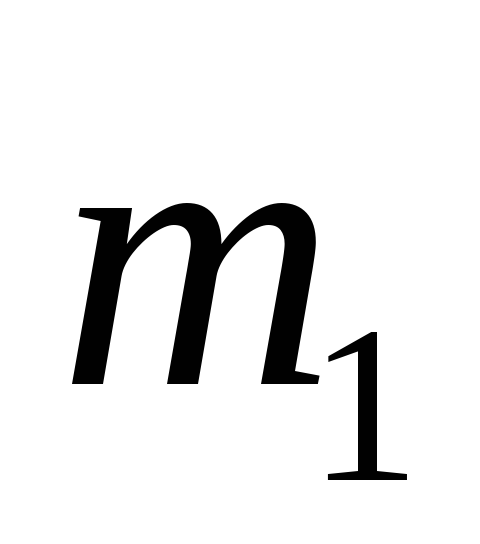 и
и
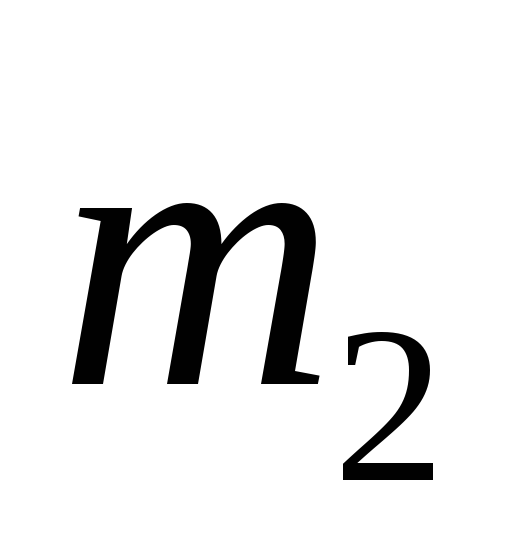 .
Угольник соединен с вертикальной
осью вращения с помощью горизонтального
цилиндрического шарнира О.
Определить угловую скорость ω
установившегося вращения, если .
Угольник соединен с вертикальной
осью вращения с помощью горизонтального
цилиндрического шарнира О.
Определить угловую скорость ω
установившегося вращения, если
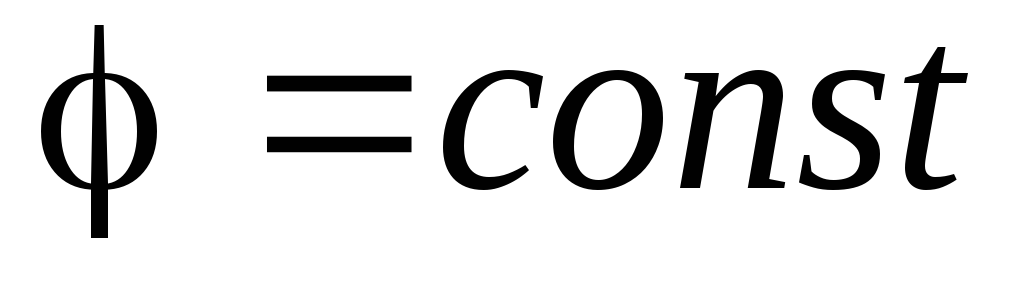 ,
ОА=ОВ=ℓ. Массой треугольника и
трением пренебречь. ,
ОА=ОВ=ℓ. Массой треугольника и
трением пренебречь.
|
|
Принцип
виртуальных перемещений
|
|
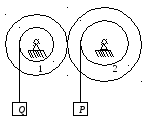
К шестерням с радиусами
 и
и
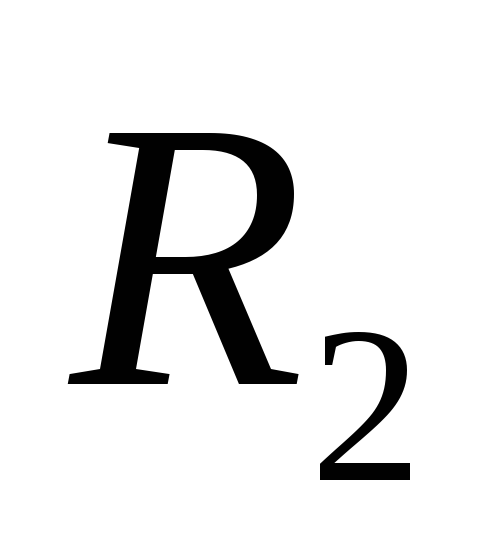 ,
находящимся в зацеплении, прикреплены
шкивы с радиусами ,
находящимся в зацеплении, прикреплены
шкивы с радиусами
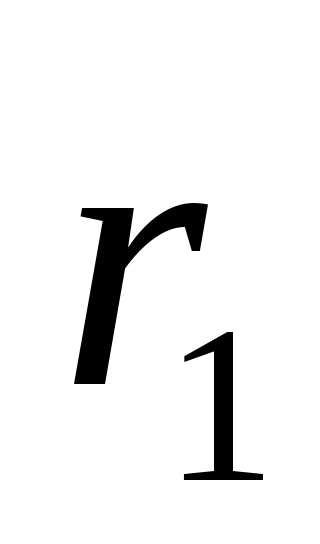 и
и
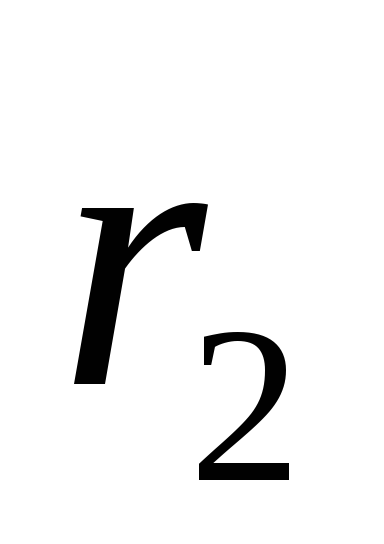 соответственно. На шкивы намотаны
гибкие невесомые нити, на которых
подвешены грузы весом P
и Q . Применив
принцип возможных перемещений, найти
отношение весов грузов P/Q,
при котором система будет в равновесии.
соответственно. На шкивы намотаны
гибкие невесомые нити, на которых
подвешены грузы весом P
и Q . Применив
принцип возможных перемещений, найти
отношение весов грузов P/Q,
при котором система будет в равновесии.
|
|
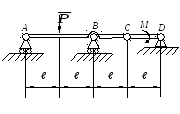
Найти
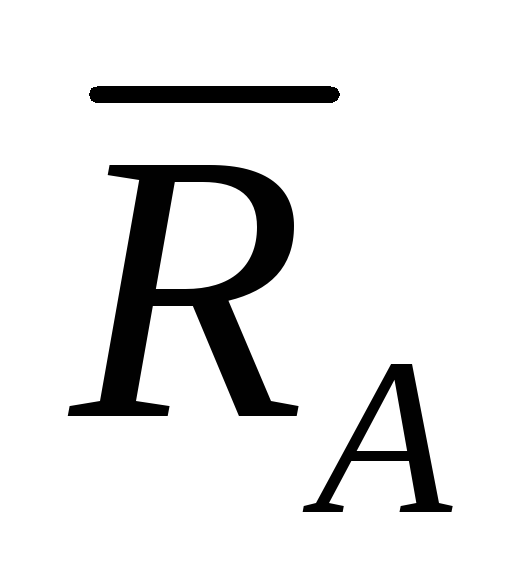 ,
используя принцип возможных перемещений.
Считать известными Р, ℓ и М. ,
используя принцип возможных перемещений.
Считать известными Р, ℓ и М.
|
|

Найти
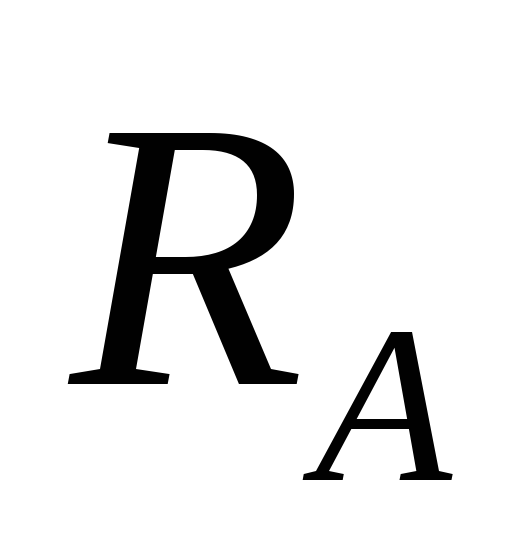 ,
используя принцип возможных перемещений. ,
используя принцип возможных перемещений.
 . .
|
|
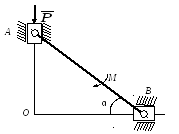
К ползуну А
эллипсографа приложена сила Р.
Используя принцип возможных перемещений,
найти момент М, приложенный к
линейке АВ длиной а, при котором
в положении равновесия линейка составит
с горизонтом угол α. Весом линейки
пренебречь.
|
|
К ползуну А
эллипсографа приложена сила Р.
Используя принцип возможных перемещений,
найти силу
 ,
приложенную к ползуну ,
приложенную к ползуну
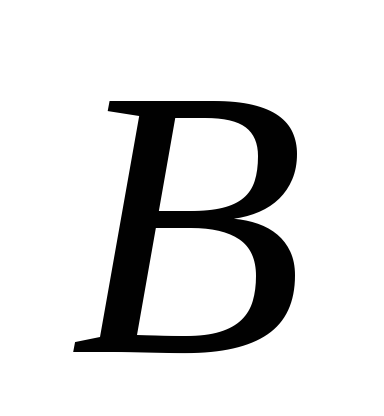 .
Длина стержня АВ равна а. В
положении равновесия стержень .
Длина стержня АВ равна а. В
положении равновесия стержень
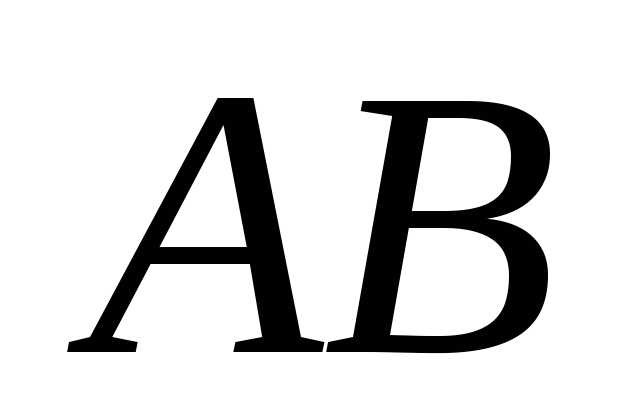 наклонен под углом α. Весом линейки
пренебречь.
наклонен под углом α. Весом линейки
пренебречь.
|
|

Кривошипно–шатунный
механизм, у которого
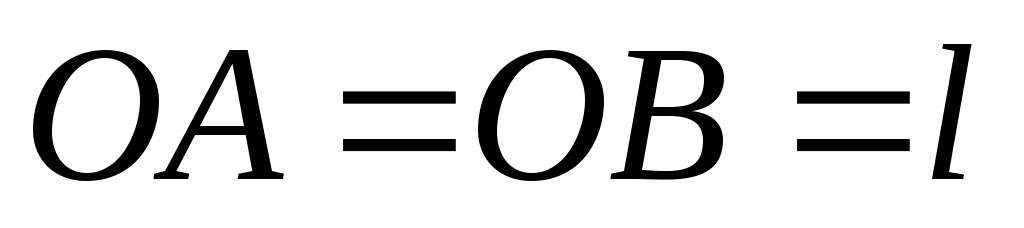 ,
расположен в горизонтальной плоскости.
Используя принцип возможных перемещений,
найти момент М, уравновешивающий силу
Р при заданном значении угла γ. ,
расположен в горизонтальной плоскости.
Используя принцип возможных перемещений,
найти момент М, уравновешивающий силу
Р при заданном значении угла γ.
|
|
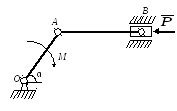
К ползуну В
кривошипно–шатунного механизма
приложена горизонтальная сила
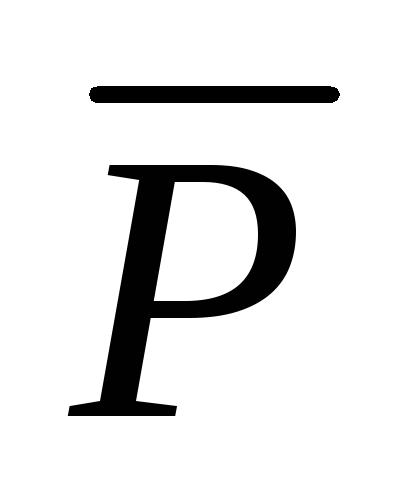 .
Используя принцип возможных перемещений,
найти какой вращающий момент надо
приложить к кривошипу ОА, чтобы
механизм находился в равновесии. ОА
= ℓ ; АВ = 2ℓ ; α = 45°.
Механизм расположен в горизонтальной
плоскости. Трением в опорах пренебречь. .
Используя принцип возможных перемещений,
найти какой вращающий момент надо
приложить к кривошипу ОА, чтобы
механизм находился в равновесии. ОА
= ℓ ; АВ = 2ℓ ; α = 45°.
Механизм расположен в горизонтальной
плоскости. Трением в опорах пренебречь.
|
|
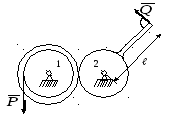
Считая известными
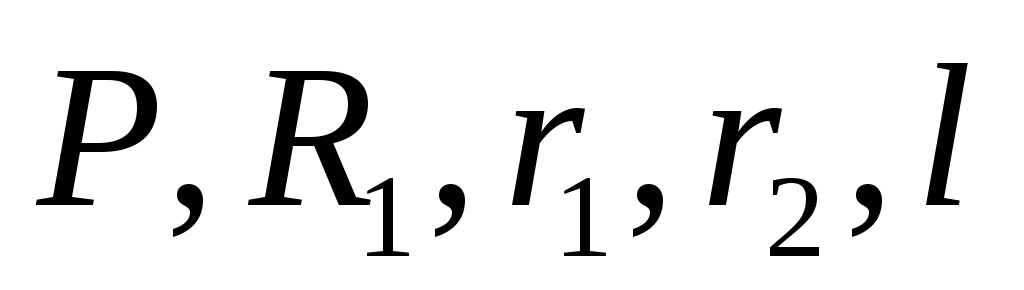 ,
с помощью принципа возможных перемещений
определить , при каком Q
система будет находиться в равновесии.
Механизм расположен в горизонтальной
плоскости. ,
с помощью принципа возможных перемещений
определить , при каком Q
система будет находиться в равновесии.
Механизм расположен в горизонтальной
плоскости.
|
|
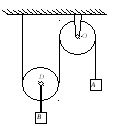
Используя принцип
возможных перемещений, определить
вес груза В для того, чтобы система,
изображенная на чертеже, находилась
в равновесии. Вес груза А равен Р,
вес блока D – Q,
весом нити и блока О пренебречь.
Нить по блокам не скользит.
|
|
Уравнения Лагранжа
II-го рода
|
|
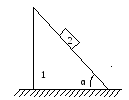
Призма 1 массы
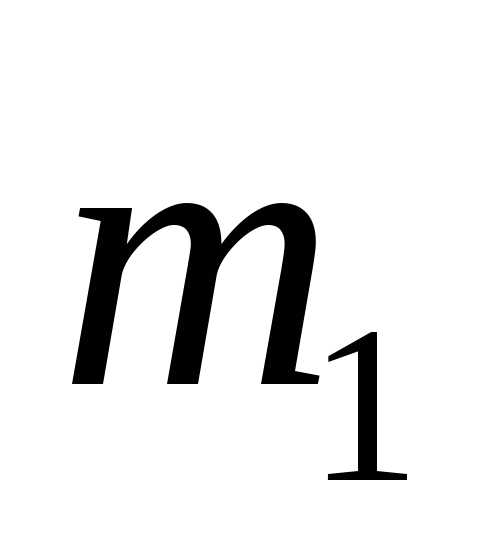 движется поступательно и прямолинейно
по гладкой горизонтальной плоскости.
По наклонной грани призмы, образующей
угол α с горизонтом, скользит груз 2.
массы
движется поступательно и прямолинейно
по гладкой горизонтальной плоскости.
По наклонной грани призмы, образующей
угол α с горизонтом, скользит груз 2.
массы
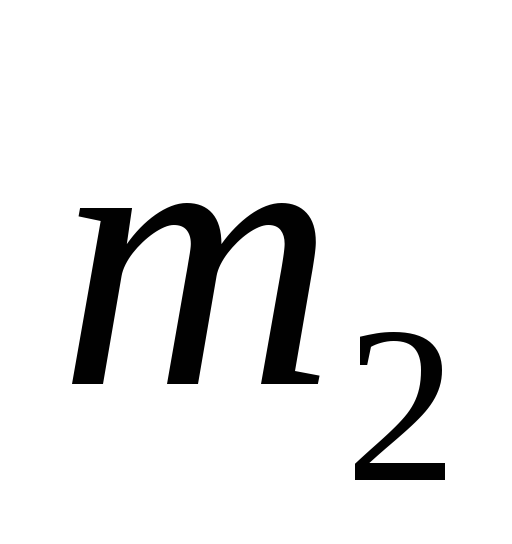 .
Выбрать обобщенные координаты и
получить выражения для кинетической
энергии системы и обобщенных сил,
соответствующих этим координатам.
При решении задачи трением между
грузом 2 и призмой 1 пренебречь. .
Выбрать обобщенные координаты и
получить выражения для кинетической
энергии системы и обобщенных сил,
соответствующих этим координатам.
При решении задачи трением между
грузом 2 и призмой 1 пренебречь.
|
|
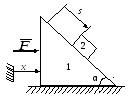
Клин 1 массы
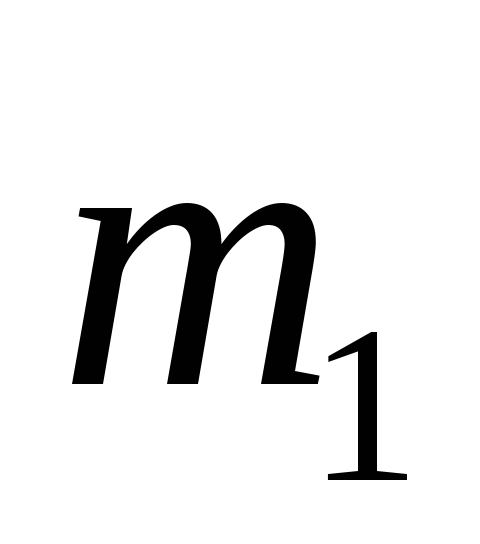 расположен на горизонтальной плоскости.
На наклонной грани клина, составляющей
с горизонтом угол α, находится тело 2
массы
расположен на горизонтальной плоскости.
На наклонной грани клина, составляющей
с горизонтом угол α, находится тело 2
массы
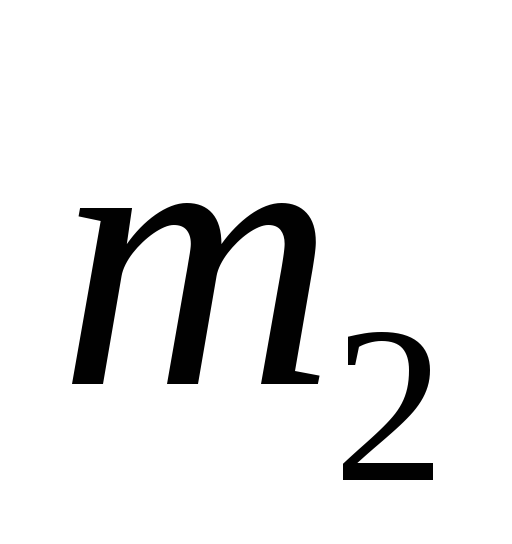 .
К клину приложена горизонтальная
сила .
К клину приложена горизонтальная
сила
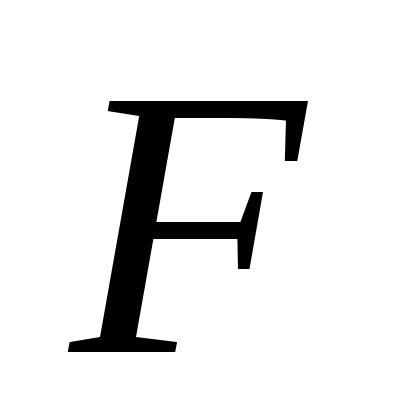 .
Принимая за обобщённые координаты
системы параметры x
и s, указанные на
рисунке, найти выражение для кинетической
энергии и обобщенных сил. Трением
пренебречь. .
Принимая за обобщённые координаты
системы параметры x
и s, указанные на
рисунке, найти выражение для кинетической
энергии и обобщенных сил. Трением
пренебречь.
|
|

Груз 1 массой
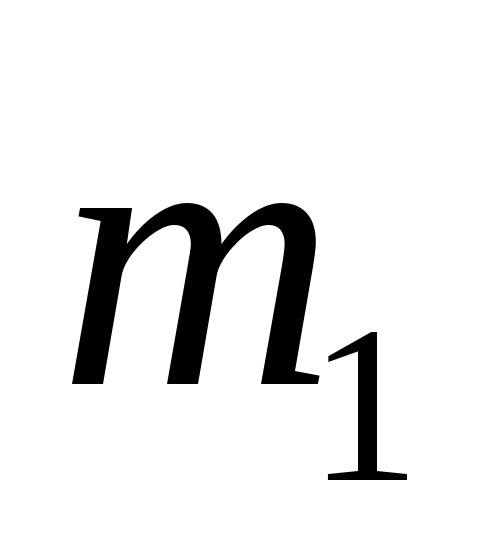 подвешен на нити к оси к оси подвижного
блока 2 массы
подвешен на нити к оси к оси подвижного
блока 2 массы
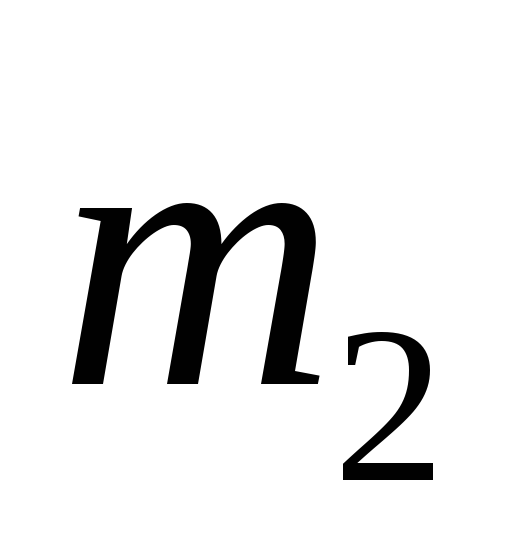 и радиуса
и радиуса
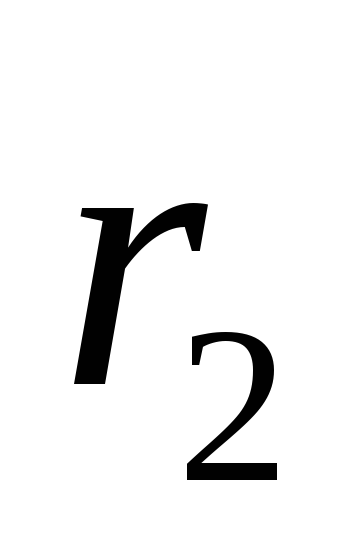 .
Этот блок охватывает другая нить, один
конец которой закреплён неподвижно,
а к второму прикреплён груз 4 массы .
Этот блок охватывает другая нить, один
конец которой закреплён неподвижно,
а к второму прикреплён груз 4 массы
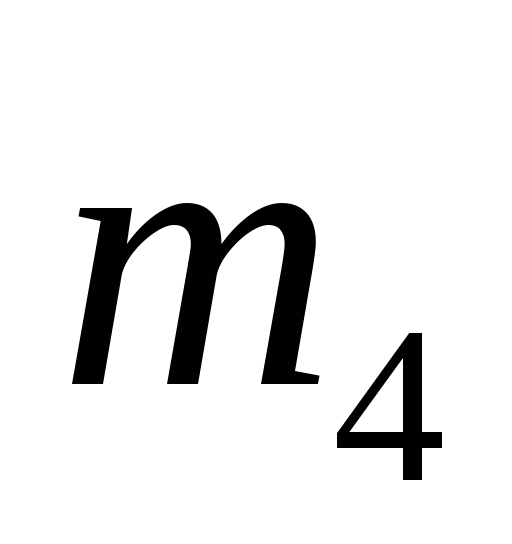 .
Выбрать обобщённую координату и
составить выражение для кинетической
энергии системы и обобщённой силы,
соответствующей выбранной координате.
При решении задачи блок 2 принять за
однородный диск, массами блока 3 и
нитей, а также трением в шарнирах
пренебречь. .
Выбрать обобщённую координату и
составить выражение для кинетической
энергии системы и обобщённой силы,
соответствующей выбранной координате.
При решении задачи блок 2 принять за
однородный диск, массами блока 3 и
нитей, а также трением в шарнирах
пренебречь.
|
|
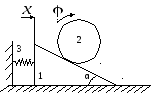
По горизонтальной
гладкой поверхности движется призма
1 массой
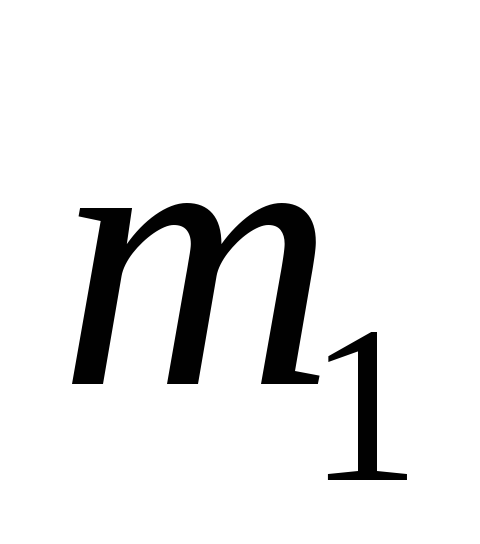 .
К призме прикреплен один конец пружины
3, коэффициент жесткости которой равен
с. Второй конец пружины прикреплен
к стене. По наклонной грани призмы,
образующей угол α с горизонтом, катится
без скольжения однородный цилиндр 2
массой .
К призме прикреплен один конец пружины
3, коэффициент жесткости которой равен
с. Второй конец пружины прикреплен
к стене. По наклонной грани призмы,
образующей угол α с горизонтом, катится
без скольжения однородный цилиндр 2
массой
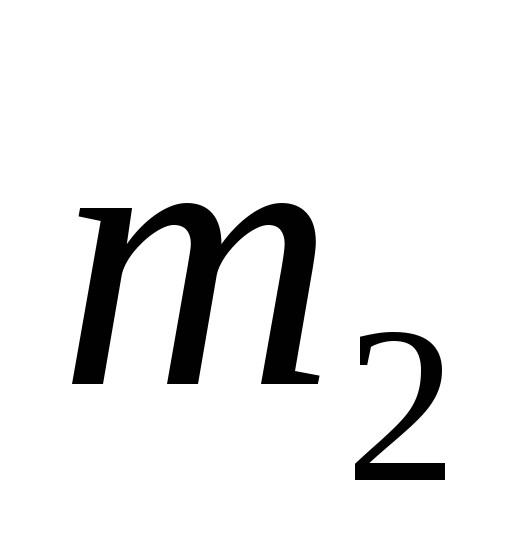 .
При .
При
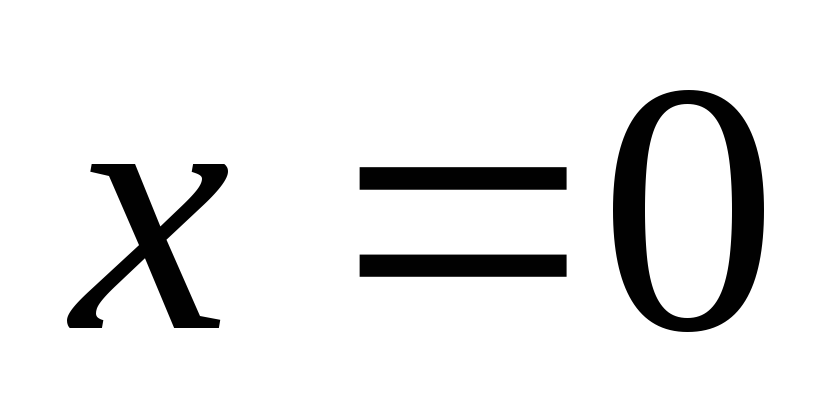 пружина не деформирована. Записать
выражения кинетической энергии и
обобщенных сил. Трением качения
пренебречь.
пружина не деформирована. Записать
выражения кинетической энергии и
обобщенных сил. Трением качения
пренебречь.
|
|
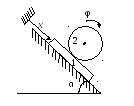
Платформа 1 массы
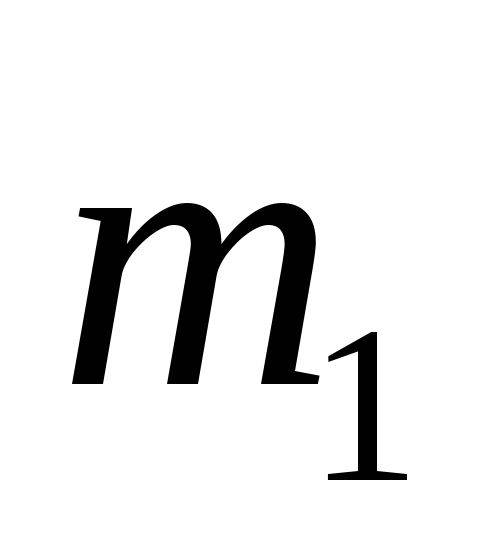 расположена на плоскости, наклонённой
к горизонту под углом α. На платформе
находится однородный сплошной цилиндр
2 массы
расположена на плоскости, наклонённой
к горизонту под углом α. На платформе
находится однородный сплошной цилиндр
2 массы
 и радиуса R. Ось
цилиндра горизонтальна. Коэффициент
трения скольжения между платформой
и наклонной плоскостью равен f.
Между платформой и цилиндром скольжение
отсутствует. Принимая за обобщённые
координаты системы параметры х и
φ, указанные на
рисунке, найти выражения для кинетической
энергии и обобщённых сил.
и радиуса R. Ось
цилиндра горизонтальна. Коэффициент
трения скольжения между платформой
и наклонной плоскостью равен f.
Между платформой и цилиндром скольжение
отсутствует. Принимая за обобщённые
координаты системы параметры х и
φ, указанные на
рисунке, найти выражения для кинетической
энергии и обобщённых сил.
|
|
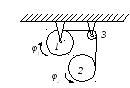
Однородные цилиндры
1 и 2 радиусов
 и
и
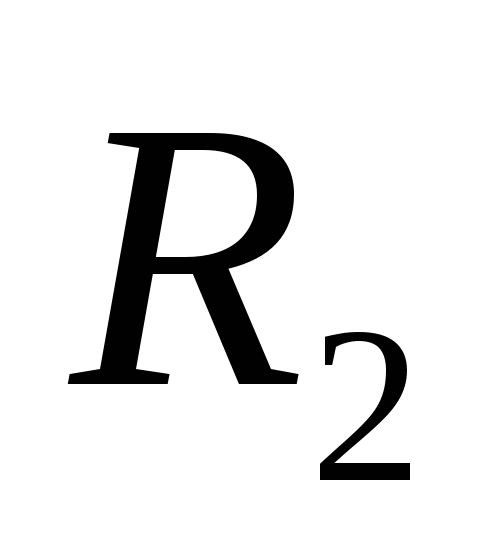 соответственно, массой
соответственно, массой
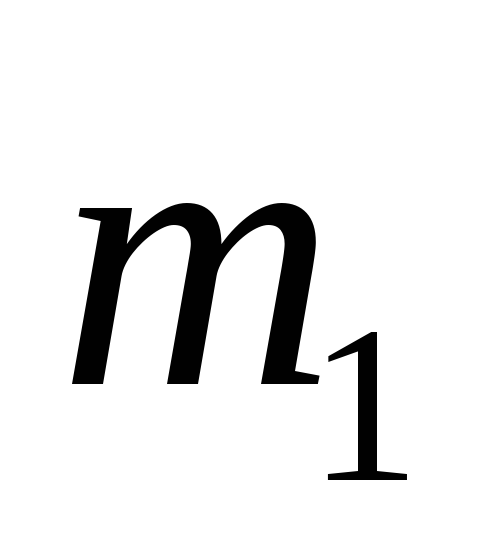 и
и
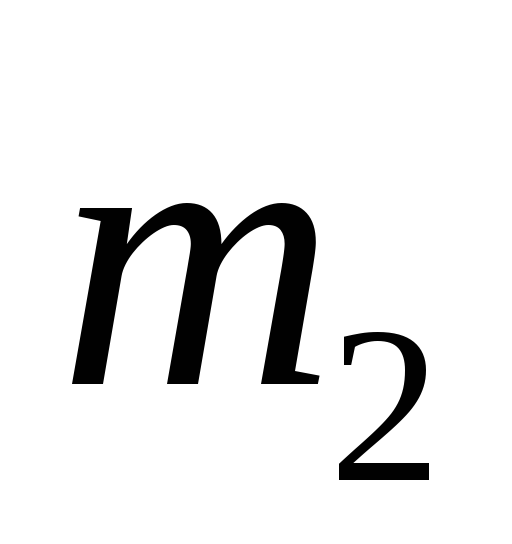 обмотаны тросом, перекинутым через
блок 3 массой
обмотаны тросом, перекинутым через
блок 3 массой
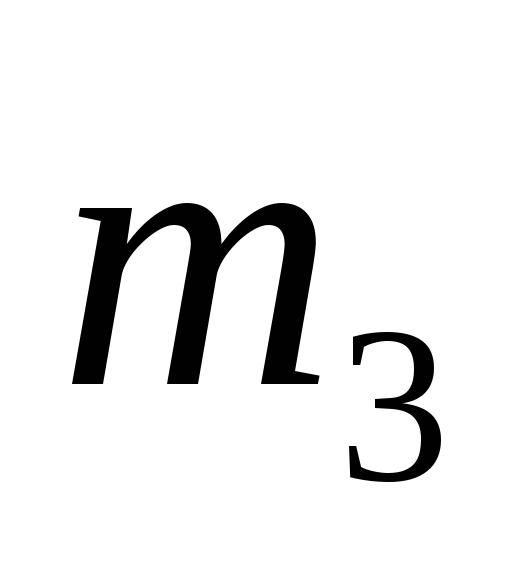 ;
блок 3 принять за однородный диск,
растяжением и массой троса пренебречь.
Трос по блоку не скользит. Выбрав в
качестве обобщенных координат углы ;
блок 3 принять за однородный диск,
растяжением и массой троса пренебречь.
Трос по блоку не скользит. Выбрав в
качестве обобщенных координат углы
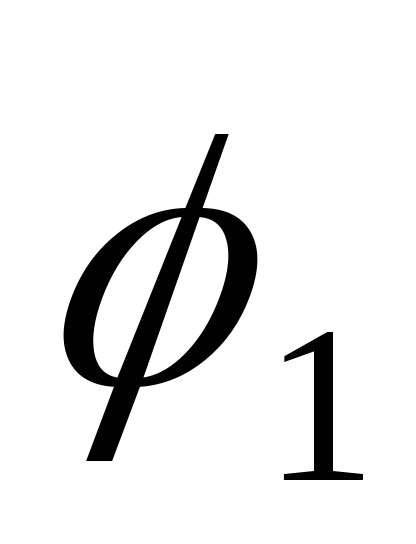 и
и
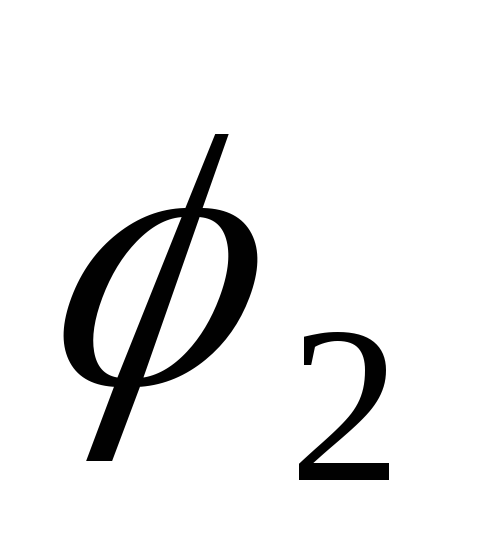 поворота цилиндров, найти кинетическую
энергию и обобщенные силы.
поворота цилиндров, найти кинетическую
энергию и обобщенные силы.
|
|

Однородный круглый
цилиндр 1 массы m,
катится без скольжения по горизонтальной
плоскости. Нерастяжимый трос, перекинутый
через блок 3, охватывает с одной стороны
цилиндр 1, а с другой – однородный
круглый диск 2 массы
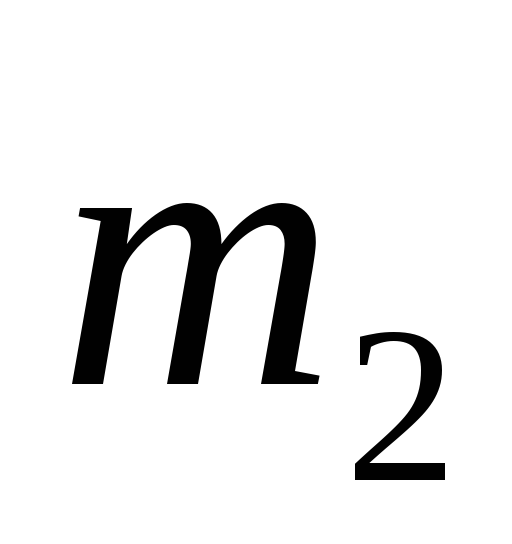 .
Приняв за обобщенные координаты .
Приняв за обобщенные координаты
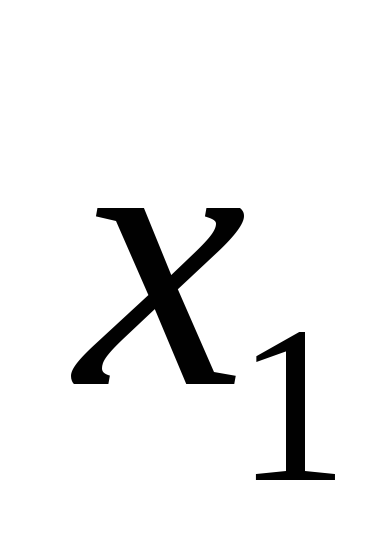 и
и
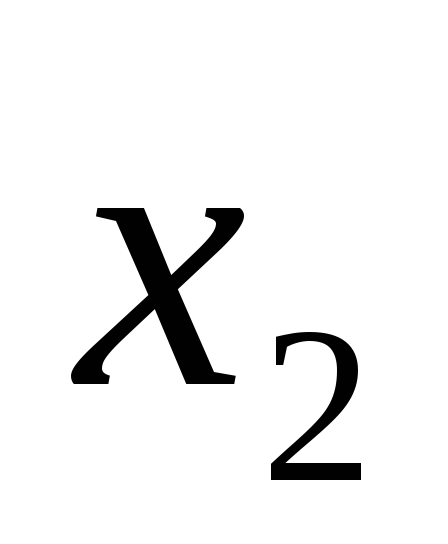 составить выражения для кинетической
энергии системы и обобщенных сил.
Массами троса и блока 3, проскальзыванием
троса по цилиндру 1 и диску 2, сопротивлением
на оси блока, а также моментом трения
качения при движении цилиндра 1
пренебречь.
составить выражения для кинетической
энергии системы и обобщенных сил.
Массами троса и блока 3, проскальзыванием
троса по цилиндру 1 и диску 2, сопротивлением
на оси блока, а также моментом трения
качения при движении цилиндра 1
пренебречь.
|
|
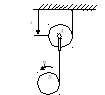
Однородные цилиндры
А и В радиуса R
и массой
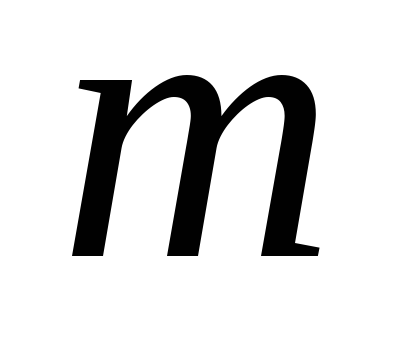 обмотаны посередине тросами, свободные
концы которых прикреплены соответственно
к потолку и к оси цилиндра А. Трением
на оси цилиндра А, растяжением и
массой тросов пренебречь. Приняв в
качестве обобщённых координат
координату оси s
цилиндра А и угол поворота γ
цилиндра В. Найти кинетическую
энергию и обобщённые силы.
обмотаны посередине тросами, свободные
концы которых прикреплены соответственно
к потолку и к оси цилиндра А. Трением
на оси цилиндра А, растяжением и
массой тросов пренебречь. Приняв в
качестве обобщённых координат
координату оси s
цилиндра А и угол поворота γ
цилиндра В. Найти кинетическую
энергию и обобщённые силы.
|
|

Плита массой
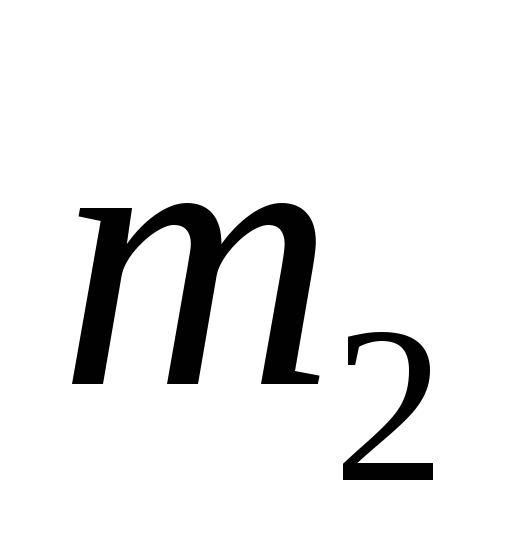 перемещается по гладкой горизонтальной
плоскости. По плите катиться без
скольжения однородный круглый цилиндр
1 массы
перемещается по гладкой горизонтальной
плоскости. По плите катиться без
скольжения однородный круглый цилиндр
1 массы
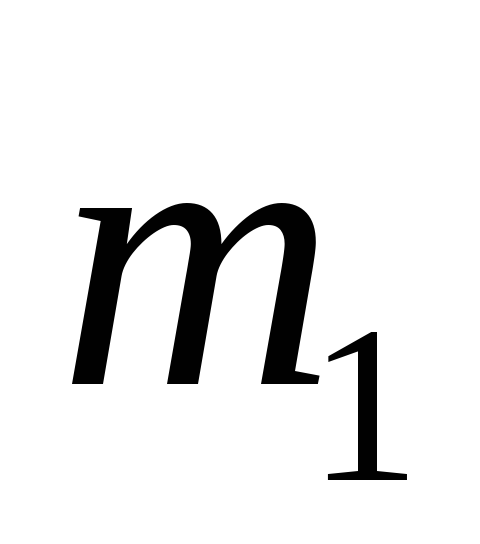 .
С осью цилиндра 1 соединен нерастяжимым
тросом, перекинутым через блок 4, груз
3 массы .
С осью цилиндра 1 соединен нерастяжимым
тросом, перекинутым через блок 4, груз
3 массы
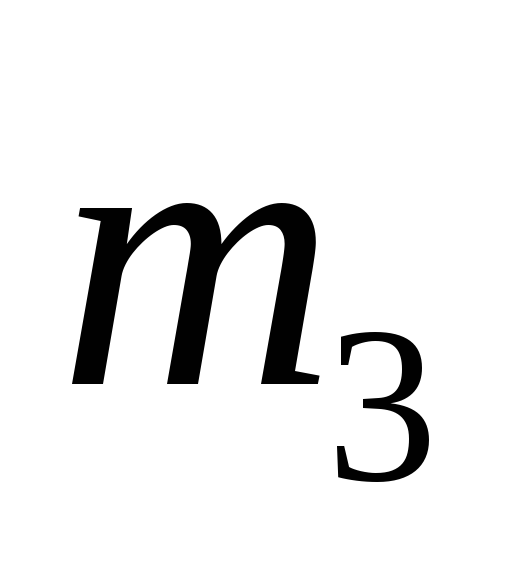 .
Груз 3 перемещается в гладком вертикальном
отверстии в плите 2. Приняв за обобщённые
координаты .
Груз 3 перемещается в гладком вертикальном
отверстии в плите 2. Приняв за обобщённые
координаты
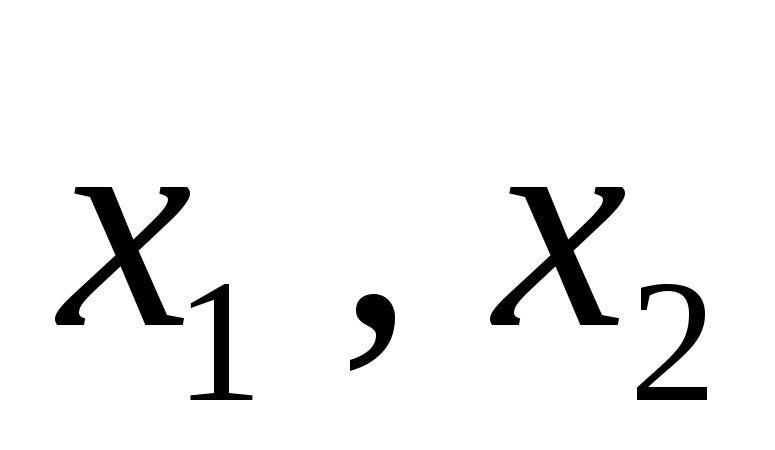 ,
составить выражения для кинетической
энергии системы и обобщённых сил.
Массами троса, блока 4, сопротивлением
в осях, а так же моментом трения качения
при движении цилиндра пренебречь. ,
составить выражения для кинетической
энергии системы и обобщённых сил.
Массами троса, блока 4, сопротивлением
в осях, а так же моментом трения качения
при движении цилиндра пренебречь.
|
|
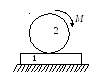
Плита 1 массой
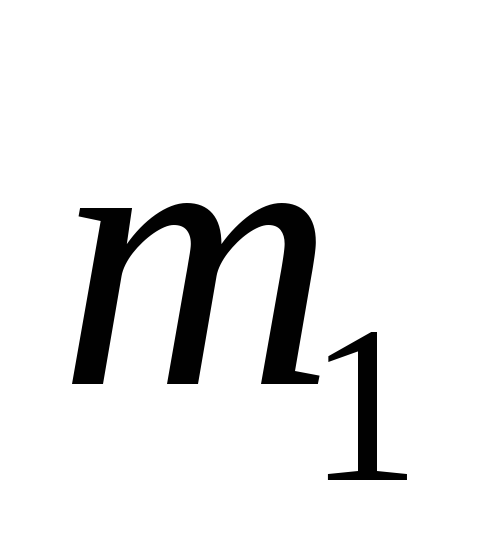 перемещается по гладкой горизонтальной
плоскости. По плите катается без
скольжения однородный цилиндр массы
перемещается по гладкой горизонтальной
плоскости. По плите катается без
скольжения однородный цилиндр массы
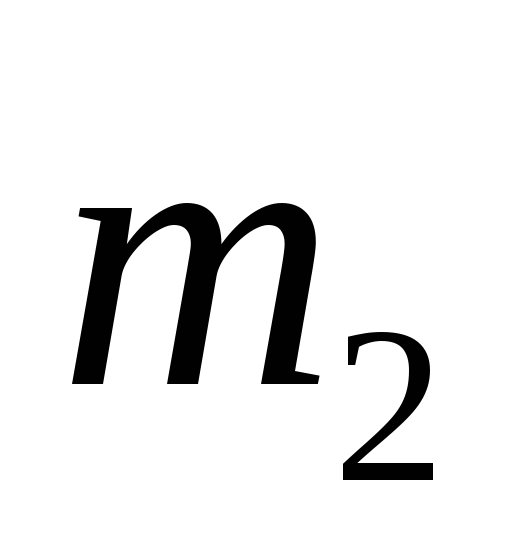 и радиуса r . К цилиндру
приложена пара сил с моментом М.
Выбрать обобщённые координаты и
записать выражения для кинетической
энергии системы и обобщённых сил.
Трением качения при решении задачи
пренебречь.
и радиуса r . К цилиндру
приложена пара сил с моментом М.
Выбрать обобщённые координаты и
записать выражения для кинетической
энергии системы и обобщённых сил.
Трением качения при решении задачи
пренебречь.
|
|
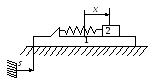
Плита 1 массой
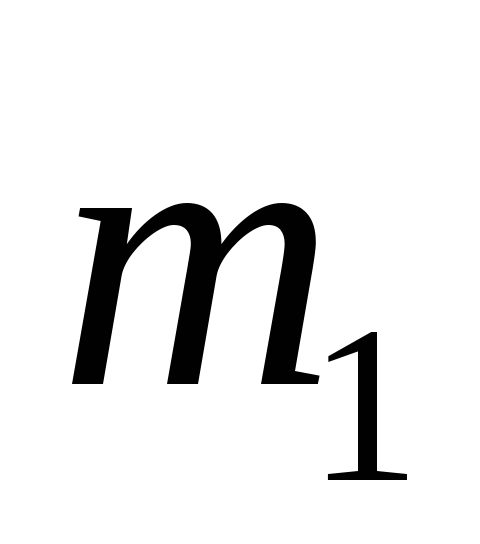 движется по гладкой горизонтальной
плоскости. К плите прикреплена одним
своим концом пружина, к другому концу
которой прикреплён груз 2 массой
движется по гладкой горизонтальной
плоскости. К плите прикреплена одним
своим концом пружина, к другому концу
которой прикреплён груз 2 массой
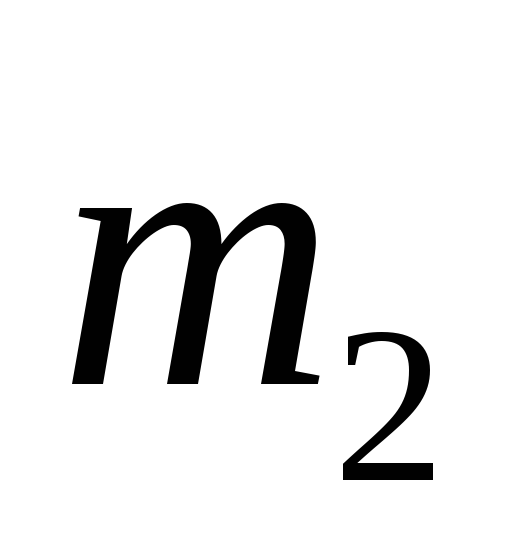 .
Коэффициент жёсткости пружины равен
c. Выбрав в качестве
обобщённых координат s
– перемещение плиты 1 и x
– перемещение груза 2 относительно
плиты, определить кинетическую энергию
системы и обобщённые силы. При решении
задачи массой пружины и трением между
грузом и плитой пренебречь. При х=0
пружина не деформирована. .
Коэффициент жёсткости пружины равен
c. Выбрав в качестве
обобщённых координат s
– перемещение плиты 1 и x
– перемещение груза 2 относительно
плиты, определить кинетическую энергию
системы и обобщённые силы. При решении
задачи массой пружины и трением между
грузом и плитой пренебречь. При х=0
пружина не деформирована.
|
|

Однородный круглый
диск 1 массой
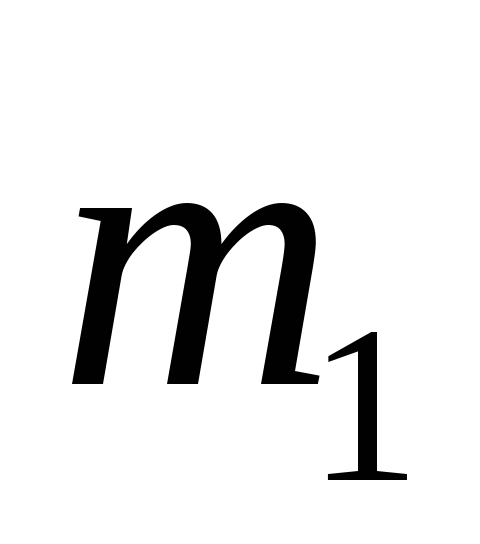 и радиуса
и радиуса
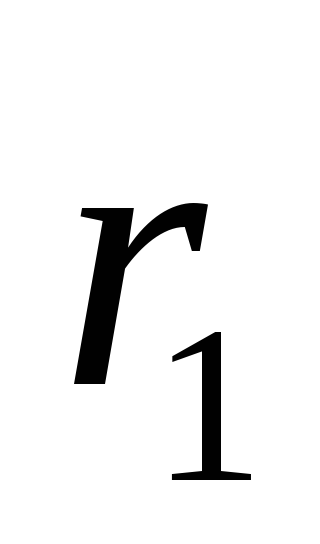 катится со скольжением по горизонтальной
плоскости. Нерастяжимый трос,
прикреплённый к оси диска, перекинут
через блок 2; а к другому концу троса
прикреплён груз 3 массы
катится со скольжением по горизонтальной
плоскости. Нерастяжимый трос,
прикреплённый к оси диска, перекинут
через блок 2; а к другому концу троса
прикреплён груз 3 массы
 .
Приняв за обобщённые координаты x
и .
Приняв за обобщённые координаты x
и
 – угол поворота диска, составить
выражение для кинетической энергии
механической системы и обобщённых
сил. Коэффициент трения скольжения
диска по плоскости – f.
Массами троса, блока 2, моментом трения
качения диска по плоскости, а также
сопротивлением на осях блока и катка
пренебречь.
– угол поворота диска, составить
выражение для кинетической энергии
механической системы и обобщённых
сил. Коэффициент трения скольжения
диска по плоскости – f.
Массами троса, блока 2, моментом трения
качения диска по плоскости, а также
сопротивлением на осях блока и катка
пренебречь.
|
|

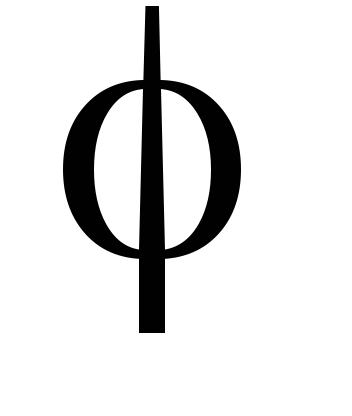
К однородному диску
массы
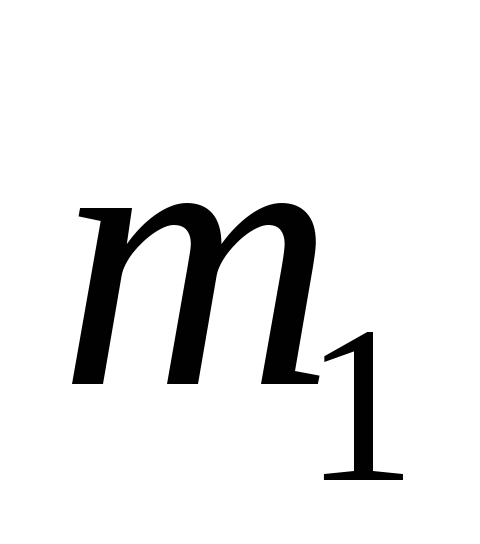 и радиуса r ,
вращающемуся вокруг неподвижной
горизонтальной оси, приложена пара
сил с моментом
и радиуса r ,
вращающемуся вокруг неподвижной
горизонтальной оси, приложена пара
сил с моментом
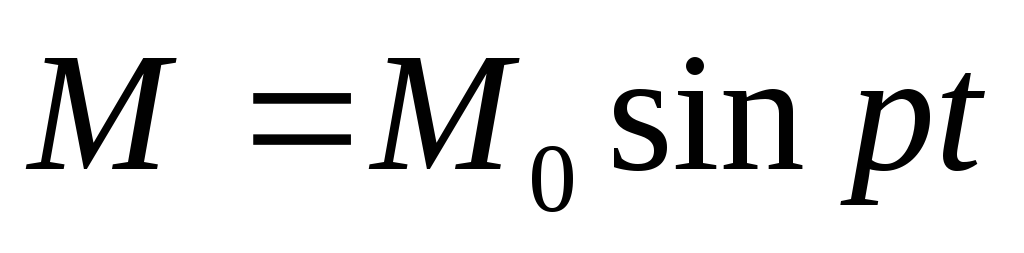 (
(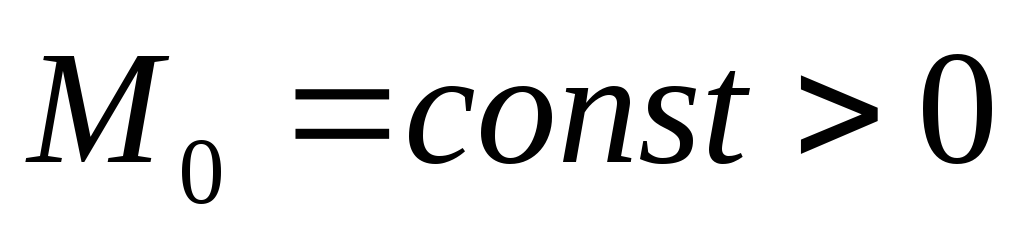 , ,
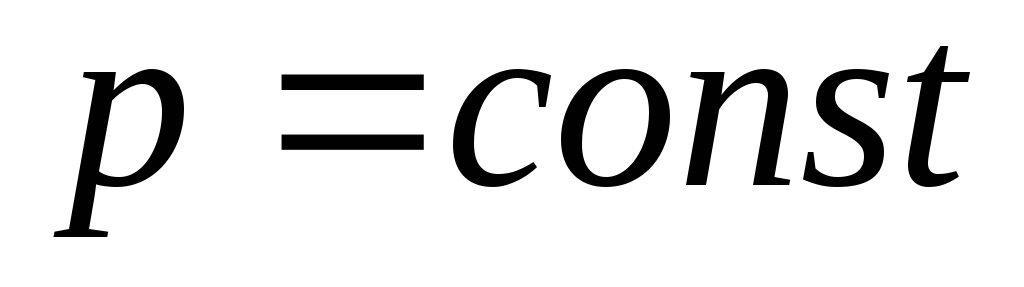 ).
На диск намотан упругий трос, коэффициент
жесткости которого равен c.
К свободному концу троса прикреплен
груз массы ).
На диск намотан упругий трос, коэффициент
жесткости которого равен c.
К свободному концу троса прикреплен
груз массы
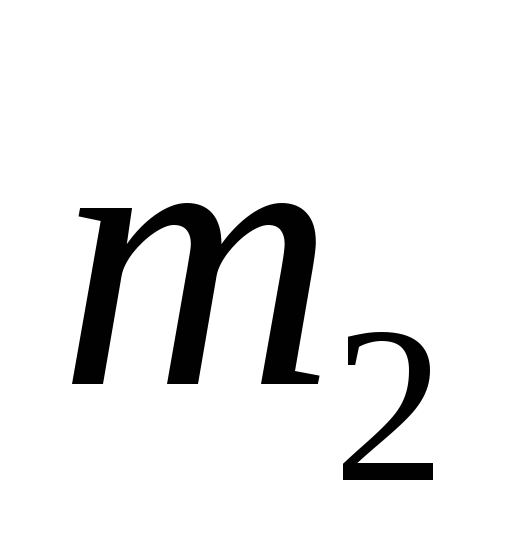 .
Пренебрегая весом троса, вычислить
кинетическую энергию системы и
обобщенные силы, соответствующие
обобщенным координатам φ и .
Пренебрегая весом троса, вычислить
кинетическую энергию системы и
обобщенные силы, соответствующие
обобщенным координатам φ и
 .
Координата .
Координата
 отсчитывается от положения статистического
равновесия груза.
отсчитывается от положения статистического
равновесия груза.
|
|
Приближенная теория
гироскопа
|
|
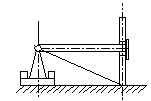
В дробилке с бегунами
каждый бегун имеет массу m=120кг,
радиус инерции относительно оси ρ =
0.4м ,радиус R = 0.5м.
Мгновенная ось вращения бегуна проходит
через середину линии касания бегуна
с дном чаши. Определить давление бегуна
на горизонтальное дно чаши, если
переносная угловая скорость вращения
бегуна вокруг вертикальной оси
соответствует
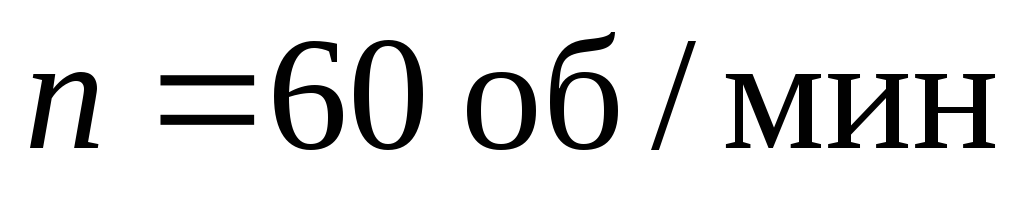 . .
|
|
Турбина, вал которой
параллелен продольной оси судна,
делает 240 об/мин. Масса вращающихся
частей 180 тонн, радиус инерции
относительно оси вращения
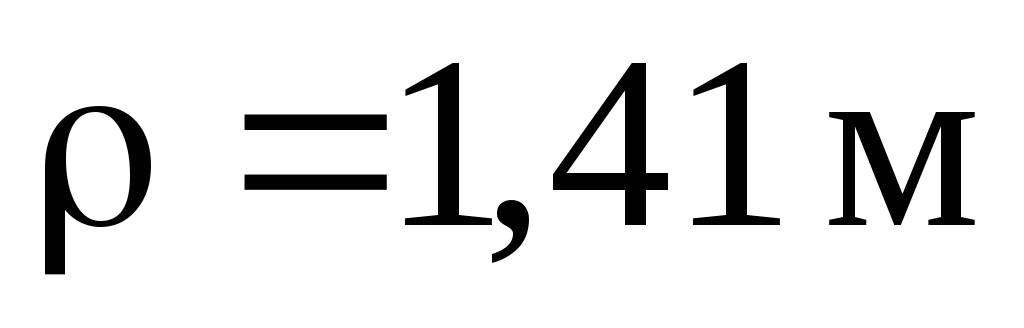 .
Определить гироскопические давления
на подшипники, если судно описывает
циркуляцию вокруг вертикальной оси,
поворачиваясь на 10° в секунду. Расстояние
между подшипниками .
Определить гироскопические давления
на подшипники, если судно описывает
циркуляцию вокруг вертикальной оси,
поворачиваясь на 10° в секунду. Расстояние
между подшипниками
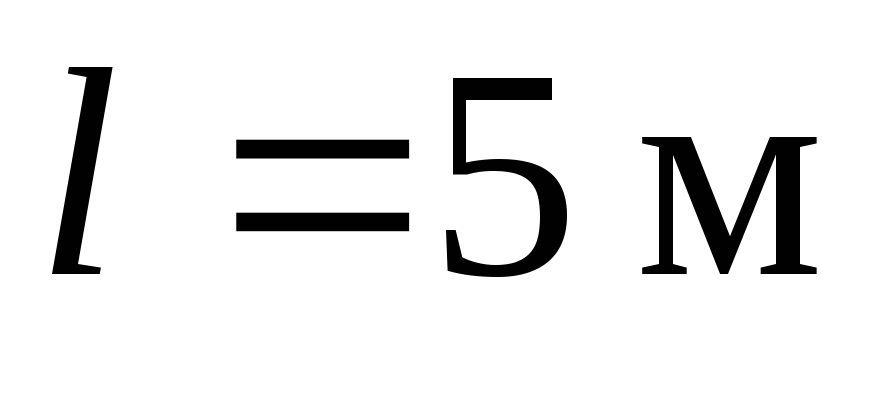 . .
|




























