
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ К ИЗУЧЕНИЮ КУРСА АЛГЕБРЫ (110
..pdf
Министерство образования и науки российской федерации
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования
«Оренбургский государственный педагогический университет»
М.И. Черемисина
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ
К ИЗУЧЕНИЮ КУРСА АЛГЕБРЫ
Часть I
Оренбург
2011
УДК 512
ББК 22.14 Ч 46
Рецензенты:
Н.А. Мунасыпов, к. ф.-м. н., доцент кафедры математического анализа и МПМ;
А.Д. Сафарова, старший преподаватель кафедры геометрии.
Черемисина М.И.
Методические рекомендации к изучению курса алгебры. Часть I
Ч46 [Текст]: учебное пособие / М.И. Черемисина, Мин-во образования
инауки РФ; Оренбург. Гос. пед. ун-т. – Оренбург: ООО «Агентство
«Пресса», 2011. – С. 27.
УДК 512
ББК 22.14
© Черемисина М.И., 2011 © ООО «Агентство «Пресса», 2011
1
Предисловие
Настоящие методические рекомендации составлены в соответствии с программой курса «Алгебра и теория чисел» для педагогических учебных заведений.
В них представлены следующие разделы:
1) Бинарные соответствия и отношения. Отношения эквивалентно-
сти.
2)Системы линейных уравнений.
3)Определители 2, 3 порядков.
В рекомендациях указан список литературы по данным разделам курса алгебры.
Методическое пособие выполняет функции обучающие и контролирующие. В связи с этим в пособии даются не только варианты контрольных работ (10 вариантов по 8 задач), но и предложен образец выполнения контрольной работы с подробным теоретическим обоснованием. Методические указания к выполнению каждого типа заданий позволяют студентам лучше ориентироваться в теоретическом материале и способствуют наиболее рациональному выбору решения каждой задачи.
Учебное пособие будет полезным студентам физикоматематического факультета, учителям математики, учащимся старших классов средних школ.
2
Рабочий план по курсу алгебры для студентов-заочников
(I часть)
№ |
|
Количество часов |
||
Наименование тем и разделов |
|
Практич. |
||
п/п |
Лекции |
|||
|
занятия |
|||
|
|
|
||
|
|
|
|
|
1. |
Множество. Операции над множествами и их основ- |
2 |
2 |
|
|
ные свойства. Прямое произведение двух множеств. |
|||
|
|
|
||
|
|
|
|
|
2. |
Бинарное отношение. Отношение эквивалентности. |
2 |
2 |
|
|
Функции (отображения). Отношения порядка. |
|||
|
|
|
||
|
|
|
|
|
3. |
Системы линейных уравнений с двумя и тремя пе- |
|
|
|
|
ременными. Равносильность систем линейных урав- |
|
|
|
|
нений и элементарные преобразования систем. Ре- |
2 |
2 |
|
|
шение систем линейных уравнений методом Гаусса. |
|||
|
|
|
||
|
Определители 2-ого и 3-его порядков. Решение си- |
|
|
|
|
стем линейных уравнений методом Крамера. |
|
|
|
|
|
|
|
|
|
Всего |
6 |
6 |
|
|
|
|
|
|
Литература
1.Антонов Н.П., Выгодский М.Я., Никитин В.В., Санкин А.И., Сборник задач по элементарной математике. – М., Гостехиздат, 1958.
2.Варпаховский Ф.Л., Солодовников А.С. Задачник-практикум по алгебре. Ч.1. М., Просвещение, 1982.
3.Виленкин Н.Я., Гутер Р.С., Шварцбурд С.И., Овчинский Б.В., Ашкиндзе В.Г. Алгебра. – М., Просвещение, 1972.
4.Гельфонд С.И., Гервер М.Л., Кириллов А.А., Константинов Н.Н., Кушниренко А.Г. Задачи по элементарной математике. – М., Наука, 1965.
5.Куликов Л.Я., Москаленко А.И., Фомин А.А. Сборник задач по алгебре и теории чисел. – М., Просвещение, 1993.
6.Курош А.Г. Курс высшей алгебры. – М., Наука, 1968.
7.Нешков К.И., Пышкало А.М., Рудницкая В.Н. Множества, отношения, числа, величины. Пособие для учителей – М., Просвещение, 1978.
8.Столл Р. Множества. Логика. Аксиоматические теории – М., Просвещение, 1968.
3
Демонстрационный вариант
|
|
|
З а д а ч а |
1 . |
|
|
Даны |
множества: |
|
|
A x |
|
x2 |
8x 15 0 , |
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
B x / |
|
x 3 |
|
4 и C x / |
|
x 2 |
|
3 . Найти ( A B) C' |
и B \ A . |
|
||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
Р е ш е н и е . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
1) Зададим множества А, В, С числовыми |
у |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
промежутками. Решим неравенство x2 8x 15 0 |
|
|
|
|
|
|
|
||||||||||||||||||||||||
графически |
|
|
|
(ветви |
параболы |
y x2 8x 15 |
|
|
|
|
|
|
|
||||||||||||||||||
направлены |
|
вверх, т. к. |
|
a 0, |
корни трехчлена |
|
|
|
|
|
|
|
|||||||||||||||||||
|
x2 8x 15 |
|
по теореме Виета: |
|
x |
3 , x |
2 |
5 ). Зна- |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
О |
|
|
|
3 |
5 |
х |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
чение трехчлена |
x2 8x 15 |
|
|
меньше |
|
нуля при |
|
|
|
|
|
|
|
||||||||||||||||||
3 x 5, |
|
|
|
получим |
|
|
|
|
A (3, 5) . |
Решив |
|
|
|
|
неравенство |
||||||||||||||||
|
x 3 |
|
4 4 x 3 4 1 x 7 , получим: |
B 1, |
7 . |
Решив нера- |
|||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
венство |
|
x |
|
2 |
|
3 |
x 2 3 |
|
|
|
x 5 |
|
, получим: C 8, 1 5, . |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
3 |
|
|
|
x 1 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
2) Изобразим множества А и В на числовой прямой: |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
–1 |
|
|
|
|
|
3 |
|
5 |
7 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Объединение множеств А и В есть часть числовой прямой, где имеется хо-
тя бы одна штриховка, т. е. A B 1, 7 .
По определению дополнения C ' ( 1, 5) , обратим внимание на то,
что числа 1 и 5 принадлежат множеству С, значит, не принадлежат мно-
жеству C ' . Изобразим множества A B и C ' на числовой прямой:
|
|
|
5 |
|
x |
–1 |
|
||||
|
|
||||
|
|
|
|||
Пересечение A B и C ' |
есть часть числовой прямой, где имеются обе |
||||
штриховки, т. е. интервал ( 1, 5) . Итак, |
A B C ' ( 1, 5) . |
||||
4

3) Изобразим множества A B и C ' на числовой прямой:
–1 |
3 |
5 |
7 |
x |
|
По определению разности множеств В и А в B \ A войдут все числа, принадлежащие В, но не принадлежащие А, т. е. часть числовой прямой, где имеется штриховка множества В, но нет штриховки множества А, т. е.
B \ A 1, 3 5, 7 . Обратим внимание на то, что числа 3 и 5 не принад-
лежат множеству А, значит, они войдут в разность B \ A .
З а д а ч а 2 . Изобразить на координатной плоскости элементы прямого (декартова) произведения множеств А и В, если:
а) A 1, 2, 3 , B 4, 5 ;
б) A 1, 3 , B 4, 5 ;
в) A 1, 2, 3 , B R .
Р е ш е н и е . Так как множества А и В – числовые множества, то элементами декартова произведения этих множеств будут упорядоченные пары чисел. Изображение каждой пары чисел точкой на координатной плоскости позволяет получить фигуру на этой плоскости.
а) Перечислим пары, принадлежащие прямому произведению множеств А и В:
A B (1, 4), (1, 5), (2, 4), (2, 5), (3, 4), (3, 5) .
Каждую пару чисел изобразим точкой на координатной плоскости, получим изображение декартова произведения A B – 6 точек плоскости.
б) Множество А содержит бесчисленное множество чисел из проме-
жутка 1, 3 . Поэтому и декартово произведения A B будет содержать бесконечное множество упорядоченных пар, у которых вторая координата равна 4 или 5, а первая – любое действительное число из промежутка от 1 до 3. Следовательно, изображением декартова произведения будут два о т-
резка, параллельных оси Ох.
5

В этом случае множество В совпадает со множеством R действительных чисел, поэтому декартово произведения A B будет содержать бесконечное множество упорядоченных пар, у которых первая координата равна 1 или 2, а вторая – любое действительное число. Следовательно, изображением декартова произведения будут три прямые, параллельные оси Оу.
а) |
|
|
|
|
|
б) |
|
|
|
|
в) |
|
|
||
у |
|
|
|
|
у |
|
|
|
|
у |
|
|
|||
5 |
|
|
|
|
5 |
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|||||
4 |
|
|
х |
|
4 |
|
|
|
|
х |
4 |
|
|
|
х |
|
|
|
|
|
|
|
|
||||||||
O 1 2 3 |
|
|
O 1 |
3 |
|
O |
1 |
2 |
3 |
||||||
|
|
|
|
|
f : R R , |
||||||||||
З а д а ч а |
3 . Доказать, что |
заданное соответствие |
|||||||||||||
x x2 |
4x 7 является отображением, |
и выяснить, какими свойствами |
|||||||||||||
оно обладает. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Р е ш е н и е . Бинарное соответствие f : X Y |
называется отобра- |
||||||||||||||
жением |
X Y , |
если оно всюду определено и функционально, |
т. е. для |
||||||||||||
x X |
существует образ |
y Y (всюду определено) |
и для x X суще- |
||||||||||||
ствует |
не |
более |
одного |
образа |
y Y |
(функционально). По |
|
условию |
|||||||
f : R R , |
причем |
для |
любого |
x R можно определить образ |
|||||||||||
y x2 4x 7 R , т. |
е. f |
всюду определено. Кроме того, для всякого |
|||||||||||||
x R найдется только одно значение |
y x2 4x 7 R , т. е. f |
– функци- |
|||||||||||||
онально. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Итак, |
f : R R , x x2 4x 7 является отображением (функци- |
||||||||||||||
ей). Выясним, какими свойствами обладает это отображение.
6

Отображение f : X Y называется инъективным, если для y Y
существует не более одного прообраза x X . В нашем же случае, напри-
мер, y 7 |
при x |
0 и |
x |
2 |
4 ( y x2 4x 4 3 y (x 2)2 3; |
|
|
1 |
|
|
|
|
|
y(0) (0 2)2 3 7 |
и |
y( 4) ( 4 2)2 3 7 ). Значит, |
f : R R , |
|||
x x2 4x 7 не является инъективным. |
|
|||||
Отображение f : X Y |
называется сюръективным, если для y Y |
|||||
существует хотя бы один прообраз x X . Так как, например, ни для како-
го x R |
y 0 , |
|
то |
для |
0 R не существует прообраза в R . Значит, |
|||||||||
f : R R , |
|
x x2 4x 7 не является сюръективным. |
|
|||||||||||
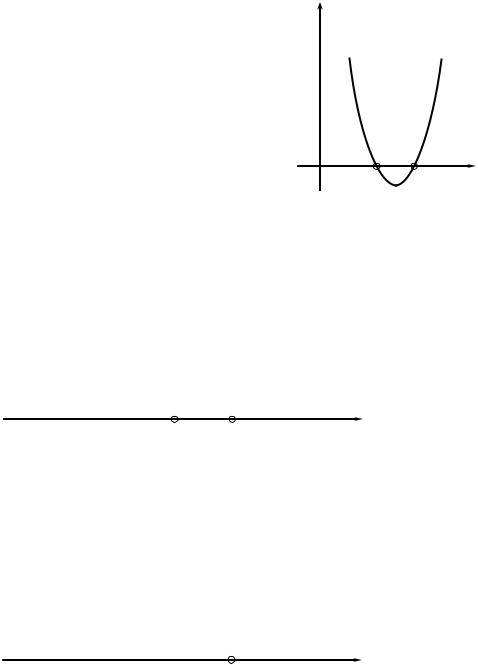
Эту задачу можно решить геометрически. Построим график соответ- |
||||||||||||||
|
|
|
у |
|
|
|
ствия: y x2 4x 7 y (x 2)2 3. Из |
гра- |
||||||
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
фика соответствия видно, что у любого |
x R |
|
|
|
|
|
|
|
|
|
|
|
|
|
есть единственный образ y R , следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
это соответствие является отображением R R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
4 |
|
|
|
(функцией). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
Из графика соответствия видим также, что |
|||
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
различным x1 3 R , x2 1 R отвечает один |
|||||
|
|
|
|
|
|
|
|
|
у0 |
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
1 |
|
|
х |
образ y 4 R , следовательно, это отображение |
|||||
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|||
х2 –2 |
х1 О 1 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
не является инъективным. Из графика отображе- |
|
ния видно, что для |
y0 2 R не существует ни одного прообраза x R , |
|||||||||||||
следовательно, это отображение не является сюръективным. |
|
|||||||||||||
З а д а ч а |
4 . На множестве Z задано бинарное отношение : |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
a b (a b) 7 . |
|
Доказать, |
что |
|
является отношением эквивалентности, и найти |
|||||||||||
классы эквивалентности. |
|
|||||||||||||
7

Р е ш е н и е . Напомним определение.
Определение. Бинарное отношение , заданное на множестве А,
называется отношением эквивалентности, если:
1)рефлексивно: ( x A) x x ,
2)симметрично: ( x, y A) x y y x ,
3)транзитивно: ( x, y, z A) x y y z x z .
Проверим, |
что |
бинарное |
отношение |
на множестве z : |
||
a b (a b) 7 обладает свойствами 1 – 3: |
|
|
||||
1) |
( a Z )a a 0 , а 0 7 a a – рефлексивно; |
|
||||
2) |
( a, b Z ) , если a b (a b) 7 a b 7q b a 7( q) |
|||||
(b a) 7 – симметрично; |
|
|
|
|||
3) |
( a, b, |
c Z ) , |
если a b b c (a b) 7 (b c) 7 a b |
|||
7q1 b c 7q2 |
, |
сложив |
эти |
равенства, |
получим: |
|
a c 7(q1 q2 ) (a c) 7 a c – транзитивно. Доказали, что – отношение эквивалентности.
Всякое отношение эквивалентности, заданное на множестве, разбивает это множество на классы эквивалентности.
Определение. Классом эквивалентности, порожденным элементом a A, называется множество таких элементов b A , которые связаны с
а отношением : |
|
b |
|
b A b a . |
|
a |
|||||
|
|||||
|
|
|
|
|
В нашем случае a b b Z (b a) 7 , например:
1 ..., 13, 6, 1, 8, 15, ... , 4 ..., 10, 3, 4, 11, 18, ... .
Замечаем, что в каждый класс эквивалентности попадают целые числа, имеющие при делении на 7 одинаковые остатки. Так как при делении на 7 возможны остатки 0, 1, 2, 3, 4, 5, 6, то получим классы эквивалентно-
сти 0 , 1 , 2 , 3 , 4 , 5 , 6 :
8

... |
... |
... |
... |
... |
|
... ... |
||||||||||||||
14 |
13 |
12 |
11 |
10 |
9 |
8 |
||||||||||||||
7 |
6 |
5 |
4 |
3 |
2 |
1 |
||||||||||||||
0 |
1 |
2 |
3 |
4 |
|
5 |
6 |
|||||||||||||
7 |
8 |
9 |
10 |
11 |
12 |
13 |
||||||||||||||
14 |
15 |
16 |
17 |
18 |
|
19 |
20 |
|||||||||||||
... |
... |
... |
... |
... |
|
... ... |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
2 |
|
3 |
4 |
|
5 |
|
6 |
|
||||||||
Напомним основные понятия теории определителей. Пусть дана квадратная матрица А n-го порядка. Сопоставим матрице А определенное число, которое будем называть определителем (детерминантом) этой матрицы.
|
|
|
|
a |
a |
... a |
1n |
|
|
|
|
|
|
a |
a |
... a |
1n |
|
|||
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
11 |
12 |
|
|
|
|
|
|
11 |
12 |
|
|
|||||
|
|
|
|
A a21a22 ... a2n |
|
|
A |
|
a21a22 ... a2n |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an1an2 ... an n |
|
|||||
|
|
|
|
an1an2 ... an n |
|
|
|
|
|
|
|||||||||||
|
|
Другие обозначения определителя: |
|
A |
|
det A. По определению |
|||||||||||||||
|
|
||||||||||||||||||||
A |
|
( 1)t a |
a |
... a |
|
, |
где |
t |
– |
число |
инверсий в перестановке |
||||||||||
|
|
||||||||||||||||||||
|
|
n! |
1 1 |
2 2 |
n n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( 1 , 2 , ... n ) . В приложениях часто встречаются определители второго и третьего порядков.
З а д а ч а 5 . Решить систему двух линейных уравнений с двумя не-
2x 3y 7,
известными по формулам Крамера: Решение показать графи-
5x 2 y 8 .
чески.
|
x |
|
||
x |
|
|
; |
|
гл. |
||||
|
|
|||
|
|
|
||
Р е ш е н и е . y |
y |
; – формулы Крамера. Найдем гл., x , y : |
||
гл. |
||||
|
|
|||
|
|
|
||
гл. 0
9
