
Распространение монохроматических волн в нелинейных средах (110
..pdf
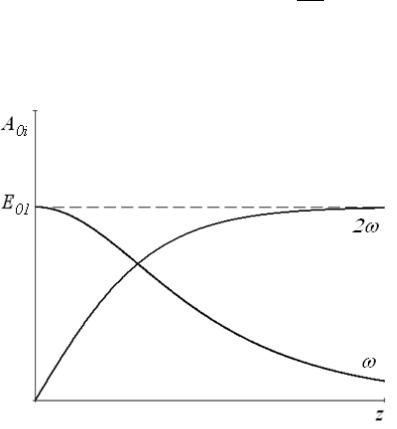
наблюдаются пространственные биения амплитуды второй гармоники |
|||||||||
|
рис. 1, кривая 2). Длина, на которой амплитуда гармо- |
||||||||
|ники| ~достигает| /2первого|( |
максимума, |
|
называется |
|
длиной |
когерентного |
|||
взаимодействия и равна: |
2 | |
| |
|
4| |
| |
. |
|
||
ког |
|
|
|
(3.14) |
|||||
|
|||||||||
Максимум амплитуды второй гармоники на этой длине равен:
2
, | |. (3.15)
Пользуясь простыми формулами, полученными выше, можно дать ответ на важный вопрос в теории нелинейных волн: при какой дисперсии амплитуда второй гармоники остаётся много меньше амплитуды основной волны, т.е. при какой дисперсии нелинейный процесс генерации второй гармоники является слабым. Потребовав, , , находим из (3.15) условие,
налагаемое на сильную дисперсию нелинейной среды:
| |
| |
|
, |
ког |
нл. |
(3.16) |
|
Последнее неравенство имеет фундаментальное значение, так как оно позволяет дать количественную характеристику сильно диспергирующей нелинейной среды (по отношению к взаимодействию волн). Если выполняется обратное неравенство
| |
| |
|
, |
ког |
нл, |
(3.17) |
|
то среда является слабо диспергирующей и возможно эффективное возбуждение гармоники с большой амплитудой, порядка начальной амплитуды основного излучения . Неравенства (3.16) и (3.17) можно обобщить и на случай генерации высших гармоник.
Когда амплитуда второй гармоники становится сравнимой с амплитудой основной волны, приближение заданного поля непригодно и
21

необходимо решать полную систему уравнений (3.3) и (3.4). Для удобства представим комплексные амплитуды в виде:
(3.18)
, 1,2.
Подставляя (3.18) в уравнения (3.3) и (3.4), получаем:
, (3.19)
. (3.20)
Приравнивая действительные части, получаем:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
, |
(3.21) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
(3.22) |
||||||||||
Для мнимых частей имеем: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
, |
(3.23) |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.24) |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Обозначая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, окончательно получаем систему уравне- |
|||||||||
ний: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n , |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.25) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
(3.26) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
(3.27) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Выпишем также с учётом граничных условий (3.8) |
.законы сохранения, ко- |
||||||||||||||||||||||||||||
торые являются интегралами движения для взаимодействующих волн:
, |
(3.28) |
|
|
22 |
|
|
|
|
фазового синхронизма, |
|
|
(3.29) |
|||||||||||
При выполнении условий |
, система уравне- |
||||||||||||||||
2 |
|
|
|
|
|
. |
|
|
|
||||||||
ний (3.25)–(3.27) сильно упрощается. Из (3.29) видно, что0при |
|
имеем |
|||||||||||||||
и |
. В итоге при синхронном взаимодействии |
волн на |
|||||||||||||||
0 |
|
||||||||||||||||
основной0и удвоенной1 |
|
частотах уравнения для их амплитуд (3.25) и (3.26) |
|||||||||||||||
принимают вид |
|
|
|
|
|
|
|
|
, |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
(3.30) |
|||||
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
. |
|
|
|
(3.31) |
|||||
|
|
|
|
|
|
|
|
|
|||||||||
Используя закон сохранения полной энергии |
|
, можно про- |
|||||||||||||||
интегрировать эти уравнения: |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
|
|
|
(3.32) |
|
|
|
|
|
|
|
|
|
|
нл |
, |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.33) |
||
|
|
|
|
|
|
|
|
|
|
|
нл |
|
|
|
|||
Рис. 2. Поведение амплитуд при полной перекачке энергии основной волны во вторую гармонику
где нл – длина нелинейного взаимодействия, определяемая соотношением (3.13). Зависимости амплитуд от расстояния показаны на рис. 2. По-
лагая в (3.33) нл,
находим, что на нелинейной длине амплитуд второй гармоники достигает относительного уровня 0,76, а интенсив-
23
ность – уровня 0,58. Из рисунка видно, что при точном согласовании скоростей основной волны и второй гармоники можно получить в принципе при
на |
∞ |
|
|
|
полное преобразование энергии волны на частоте в энергию волны |
||
|
частоте . |
возникают периодические простран- |
|
|
При |
наличии расстройки |
|
|
2 |
0системы (3.25)–(3.27), получаемое при |
|
ственные биения амплитуд. Решение |
|||
этом, показывает, что в случае слабой дисперсии (см. условие (3.17)) амплитуда второй гармоники может достигать максимума, почти равного . Если дисперсия велика, то решение аналогично полученному ранее в приближении заданного поля (3.10).
4. Распадная неустойчивость волн. Параметрическое усиление и генерация
Продолжим рассмотрение нелинейных эффектов в среде с квадратичной нелинейностью. В общем случае в одном процессе взаимодействия в такой среде могут участвовать одновременно три волны с частотами
(трёхчастотное взаимодействие), причём
Волны квадратичной поляризации, возбуждаемые. |
(4.1) |
в среде на этих частотах, |
имеют амплитуды и волновые векторы, равные (см. (1.14), (1.15) и (2.11))
, |
, |
, |
(4.2) |
||||
(4.3) |
|||||||
, |
, |
, |
(4.4) |
||||
Подставляя эти выражения в правые части, |
,укороченных. |
уравнений (2.15), |
|||||
получаем следующую систему (затухание пока не учитываем): |
|||||||
|
|
|
|
|
|
, |
(4.5) |
|
|
|
|
|
|
||
24
|
|
|
|
|
|
|
|
, |
|
(4.6) |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
, |
|
(4.7) |
|
где |
2 ̂ω ω |
|
2 ̂ω ω |
||||||||
– |
|
2 ̂ω ω |
, |
||||||||
– . |
|
|
|
|
|
|
|||||
|
Первые равенства означают, как и в случае генерации |
||||||||||
гармоники, консервативность взаимодействия волн (см. (3.7)). Чтобы показать это, запишем уравнения (4.5)–(4.7) в виде
, |
(4.8) |
, |
(4.9) |
. |
(4.10) |
Видно, что правые части уравнений (4.8) и (4.9) равны между собой и равны комплексно сопряжённой правой части уравнения (4.10), взятой со знаком «–», поэтому можно приравнять левые части уравнений
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.11) |
или |
|
|
|
|
|
| | |
|
|
|
|
|
| | |
|
|
|
|
|
|
| | |
. |
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.12) |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Учитывая, что на входе в нелинейную среду волны на частотах |
имели |
|||||||||||||||||||||||||||
амплитуды |
, из (4.12) можно получить три закона сохранения, которые |
|||||||||||||||||||||||||||
называются соотношениями Мэнли – Роу: |
|
|
|
|
. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.13) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Следствием этих соотношений является закон сохранения полной энергии:
. (4.14)
25

Проведём качественный анализ возможных режимов взаимодействия с помощью соотношений Мэнли – Роу и укороченных уравнений (4.5)–(4.7).
Сначала выясним характер энергообмена между волнами. Из соотношений (4.13) можно сделать следующий важный вывод. Если энергия
волны на наивысшей частоте |
уменьшается, то она переходит одновре- |
|
менно в обе низкочастотные волны и наоборот. То есть если амплитуда |
||
уменьшается, то амплитуды |
и |
возрастают; если же амплитуда |
увеличивается, то амплитуды |
и |
падают. Такой характер взаимодей- |
ствия существенным образом сказывается на поведении волн. Предположим, что одна из трёх волн намного интенсивнее других.
Рассмотрим два различных случая: мощная высокочастотная волна частоты и мощная низкочастотная волна частоты или .
Низкочастотная мощная волна. В соответствии с соотношениями Мэнли – Роу (4.13) квадрат амплитуды (плотность энергии) низкочастотной волны можно выразить следующим образом:
. (4.15)
В результате взаимодействия волн эта величина будет изменяться следующим образом
|
|
|
, |
|
|
|
. |
(4.16) |
Если на входе среды |
|
|
||||||
то, |
как видно из (4.16), амплитуда |
|||||||
мощной низкочастотной волны в |
процессе, |
распространения изменяется не- |
||||||
значительно. Это говорит об устойчивости распространения волны, имеющей самую низкую или среднюю частоту среди трёх взаимодействующих волн.
Из соотношений (4.13) можно найти возможный размах периодических колебаний амплитуд слабых волн на частотах и :
26
0 |
|
, |
(4.17) |
|
|||
0 |
|
. |
(4.18) |
|
Таким образом, величины амплитуд слабых волн остаются того же порядка, что и на входе в среду.
Всё сказанное означает, что при данном типе взаимодействия измене-
ние амплитуд на частотах |
и |
происходит в заданном поле основного |
|
излучения, |
, т.е. при постоянной амплитуде мощной низкочас- |
||
тотной волны. Будем решать уравнения (4.6) и (4.7). Перепишем их в виде:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
|
(4.19) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
(4.20) |
||||||
Продифференцируем первое уравнение: |
. |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.21) |
||
Подставляя сюда выражения для производной |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
из (4.20) и |
из (4.19), |
|||||||||||||||||||||||||
получаем уравнение: |
|
|
0. |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(4.22) |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогичное уравнение можно получить и для |
. Решение этих уравнений |
|||||||||||||||||||||||||
имеет вид: |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
2,3, |
(4.23) |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
бб
где Bi – константы, определяемые из граничных условий, а длина биений:
|
|
|
|
/ |
. |
(4.24) |
|
б |
4 |
||||||
|
|
||||||
Из (4.23) видно, что в поле мощной низкочастотной волны слабые волны на других частотах не нарастают; их амплитуды испытывают периодические
27

пространственные биения с характерным масштабом (4.24). Наличие расстройки волновых векторов не меняет кардинальным образом протекания процесса взаимодействия: картина биений сохраняется, только частота пространственных биений возрастает.
Высокочастотная мощная волна. Пусть мощная волна имеет наи-
большую частоту . Согласно соотношениям Мэнли – Роу (4.13) она может передать всю энергию слабым низкочастотным волнам
|
высокочастотная волна |
|
(4.25) |
Иными словами, |
большой интенсивности, распро- |
||
0 |
. |
|
|
страняясь в среде с квадратичной нелинейностью, может распадаться вследствие синхронного трёхволнового взаимодействия на две низкочас-
тотные волны. Это явление распадной неустойчивости.
Чтобы выявить условия, рассмотрим начальный этап взаимодействия
волн, когда высокочастотное поле можно считать заданным: |
, |
||||||||
, |
|
. При этом можно ограничиться решением двух свя- |
|||||||
занных линейных уравнений (4.5) и (4.6), в которых |
. Если |
||||||||
учитывать диссипацию, то решение будет иметь вид: |
|
||||||||
где |
| |
и коэффициент| |
параметрического| , |
усиления |
(4.26) |
||||
|
|||||||||
| |
2,3, |
|
|||||||
|
|
|
|
|
|
/ |
|
|
|
|
|
|
|
4 |
, |
|
(4.27) |
||
|
|
|
|
/ |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ формул (4.26) и (4.27) показывает, что параметрическое усиление низкочастотных волн имеет пороговый характер по амплитуде высокочастотной волны (рис. 3). Именно экспоненциальное нарастание амплитуды (кривые 1, 2) может происходить лишь при условии Γ /4 α или
28
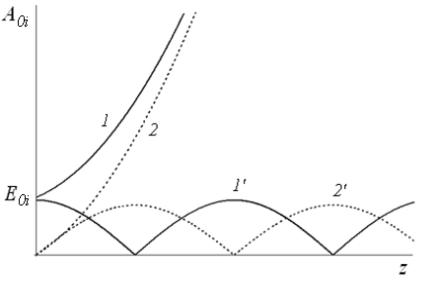
|
|
|
|
|
(4.28) |
|
Неравенство (4.28) устанавливает порог. |
||||||
параметрического усиления; оно же |
||||||
определяет область распадной неустойчивости высокочастотной волны. Чем больше потери в
|
среде |
и чем боль- |
|
|
ше рассогласование |
||
|
волновых чисел |
, |
|
|
тем выше порог па- |
||
|
раметрического |
уси- |
|
|
ления. |
Если условие |
|
|
(4.28) не достигнуто, |
||
|
то имеют место ос- |
||
Рис. 3. Зависимость амплитуд низкочастотных волн |
цилляции амплитуд |
||
от расстояния в поле высокочастотной волны ам- |
слабых волн (кривые |
||
плитуды A03 = E03 |
при E02 |
= 0 |
1′, 2′). |
|
|
|
Распадная неустойчивость приводит к разрушению высокочастотных волн, участвующих в синхронном взаимодействии с низкочастотными волнами (параметрический перенос спектра вниз). Однако это явление может быть и полезным, если его использовать для параметрического усиления слабых волн.
Параметрические волновые процессы играют большую роль в нелинейной оптике. На их основе созданы перестраиваемые по частоте источники когерентного света. Рассмотрим принцип перестройки частоты. Пусть на нелинейный кристалл падает мощная волна какой-либо фиксированной частоты , . С этой волной могут вступить в синхронное взаимодействие на квадратичной нелинейности две низкочастотные волны с частотами , и , , для которых выполняется условие
29
Начальные,амплитуды, |
этих, ислабых, |
волн определяются, |
,нулевыми. |
(4.29) |
кванто- |
выми флуктуациями поля или фоновым излучением. Вследствие
параметрического усиления в поле мощной волны частоты , |
из кристал- |
ла будет выходить когерентное излучение на других частотах |
, и , . |
Изменит теперь дисперсионные свойства кристалла в направлении распространения волн. Изменение показателей преломления можно достичь путём
изменения температуры кристалла, |
, путём изменения ори- |
ентации анизотропного кристалла, |
, (θc – угол, |
характеризующий направление синхронизма (4.29)), с помощью внешнего
постоянного электрического поля, |
|
|
|
|
(эффект Поккельса – |
||||||||||
формула (1.16)). В результате этого |
условие синхронизма (4.29) нарушает- |
||||||||||||||
|
2 |
/ |
|
|
|
|
|
|
|
||||||
ся, появляется волновая расстройка |
|
и коэффициент параметрического |
|||||||||||||
усиления, согласно формуле (4.27), для волн с частотами , |
и , умень- |
||||||||||||||
шается, а интенсивность этих волн на выходе из кристалла |
падает. Условие |
||||||||||||||
|
|
ω |
|
|
|||||||||||
синхронизма теперь будет выполняться для волн с другими частотами |
|
||||||||||||||
|
|
|
|
, |
|
|
|
, |
|
|
|
|
|
(4.30) |
|
|
|
|
|
|
|
|
). Отстройка частоты |
||||||||
(сумма частот остаётся |
постоянной: |
|
|
|
|||||||||||
|
и |
|
|
, |
|
|
|
|
|
|
|
||||
определяется условием синхронизма: |
|
|
|
|
|
|
|
|
|||||||
Раскладывая, , , , |
|
|
в ряд, |
по малым, , , |
величинам,, |
находим, , |
|
|
(4.31) |
||||||
, и |
с, учётом. |
(4.29) |
|||||||||||||
и (4.30) |
|
|
|
|
|
|
|
, |
|
|
|
|
|
||
где |
|
|
|
|
|
|
|
|
|
|
|
(4.32) |
|||
|
|
|
|
частоте |
, |
|
|
|
|
, |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
– групповая скорость на1/ |
1/ |
|
|
|
|
|
|
|
|
|
||||
, , .
Таким образом, на выходе из кристалла будем иметь когерентное излучение на новых частотах, причём перестройку частоты Ω можно осуществлять не-
30
