
Распространение монохроматических волн в нелинейных средах (110
..pdf
Сравнивая полученное выражение с (1.9), можно получить следующие выводы. Каждая из распространяющихся волн возбуждает третью гармонику (двухчастотное вырождение):
|
|
|
|
1 |
|
|
(1.18) |
и испытывает |
самовоздействие, связанное с возникновением нелинейной |
||||||
|
4 |
|
|
|
|||
поляризации на собственной частоте (одночастотное вырождение): |
|||||||
|
|
|
3 |
|
|
(1.19) |
|
Это явление ещё |
называют эффектом Керра, благодаря. |
которому диэлек- |
|||||
4 |
|
|
|
||||
трическая проницаемость зависит от интенсивности волны: |
|||||||
|
|
|
|
|
пропорциональны, |
|
(1.20) |
где коэффициенты тензора |
компонентам тензора чет- |
||||||
вёртого ранга |
̂ |
. |
|
|
̂ |
|
|
|
|
|
|
|
|||
Диэлектрическая проницаемость может также меняться под воздейст- |
|||||||
вием волны другой частоты: |
|
, |
|
||||
|
|
|
2 |
|
|
(1.21) |
|
|
|
3 |
|
, |
. |
||
|
|
|
|
|
|
||
Влияние одной волны на другую через диэлектрическую проницаемость называется кросс-модуляцией. Если диэлектрическая проницаемость изменяется под воздействием постоянного поля, то мы имеем дело с квадратичным электрооптическим эффектом (ср. с (1.16)):
В общем случае |
четырёхчастотного взаимодействия три волны с различны- |
|||
|
|
̂ ̂ 6 ̂ |
. |
|
ми частотами , |
и |
возбуждают в среде волны кубичной по полю |
||
поляризации на частотах |
|
. Соответствующий тензор |
||
кубичной восприимчивости вычисляется по формуле:
11

, , |
. (1.22) |
Высшие нелинейности. На высших нелинейностях ̂ могут развиваться эффекты генерации высших гармоник и смешения частот. Кроме того на нелинейностях нечётного порядка волны испытывают самовоздействие (нелинейная поляризация имеет ту же частоту, что и волна):
~ |
2 |
1 |
|
. |
(1.23) |
|
Сумма всех членов нелинейной части поляризации среды, ответственных за самовоздействие, описывает нелинейное изменение диэлектрической проницаемости. В изотропном случае имеем:
нл | | . |
(1.24) |
Для нелинейной добавки к диэлектрической проницаемости часто выводят выражение непосредственно из рассмотрения того или иного физического механизма нелинейного отклика среды (например, при электрострикции, нагреве при поглощении энергии волны и т.д.).
Коэффициент в формуле нелинейной поляризации для произвольной комбинационной частоты можно определить следующим образом:
! |
!… |
! |
, |
(1.25) |
!… ! |
|
|
где коэффициенты определяются из формулы (1.10).
Таким образом, в нелинейной среде могут наблюдаться явления самовоздействия и взаимодействия волн, в результате которых могут измениться частотные и угловые спектры волн, иными словами, пространственновременные законы модуляции волновых полей, заданных на входе в среду. Чтобы проанализировать развитие нелинейных электромагнитных процессов, необходимо решать при соответствующих граничных и начальных условиях уравнения Максвелла (1.1)–(1.3) совместно с нелинейными мате-
12

риальными уравнениями типа (1.6)–(1.7). Уравнения Максвелла можно свести к волновому уравнению:
|
1 |
|
|
|
4 л |
|
4 |
нл |
|
(1.26) |
|
|
|
|
|||||||
Подставляя сюда выражение для электрического поля. |
(1.8) и поляриза- |
|||||||||
ции среды |
(1.9) в виде суммы монохроматических составляющих, |
|||||||||
приходим к цепочке уравнений Гельмгольца: |
|
|
|
|
||||||
|
|
|
|
|
4 |
|
нл. |
(1.27) |
||
|
|
|
|
|||||||
В (1.27) необходимо подставить выражение для нелинейной поляризации, соответствующее исследуемому нелинейному волновому эффекту. Однако в общем случае получить решения уравнений не удаётся. Поэтому в теории нелинейных волн широко используются различные приближённые методы.
2. Методы решения нелинейных уравнений в теории волн
Метод возмущений. Предположим, что среда является слабо нелинейной: отношение величины нелинейной поляризации к величине поля на границе является малым параметром
| |
нл| |
, |
1. |
|
(2.1) |
Нелинейная поляризация |
|может| |
быть равна |
, |
, их сумме и т.д. в за- |
|
висимости от типа волнового процесса. По малому параметру можно разложить электрические поля волн
. |
(2.2) |
Подставляя (2.2) в выражение для нелинейной поляризации |
нл и учитывая |
(2.1), можно найти вид разложения нелинейной части поляризации
13

нл |
нл |
нл |
нл |
(2.3) |
где нижний индекс в скобках означает порядок малости, |
величины. Подста- |
|||
вим выражения (2.2) и (2.3) в уравнение (1.27) и удержим сначала линейные члены
|
|
|
|
|
|
|
|
(2.4) |
Найдём отсюда нулевое приближение поля |
|
0.В нулевом приближении |
||||||
(2.4) волны, падающие на границу среды, распространяются. |
как бы |
в от- |
||||||
сутствие нелинейности. |
|
|
|
|
||||
Далее подставим в уравнение поле |
с возмущением |
: |
|
|||||
|
|
|
4 |
4 |
нл. |
(2.5) |
||
В силу (2.4) |
||||||||
|
|
|
|
|
нл, |
|
(2.6) |
|
|
|
|
|
|
|
|||
где нелинейность в правой части будет иметь вид (см. (1.6))
нл |
, |
(2.7)
.
Удерживая члены первого порядка малости (с μ в первой степени), получаем уравнение
|
|
|
4 |
нл , |
|
нл |
, |
(2.8) |
|||
|
|
. |
|||
Таким образом, нелинейная добавка в правой части уравнения зависит
только от известного нулевого приближения поля |
. В следующем при- |
14 |
|

ближении (2.8) в результате возбуждения волн нелинейной поляризации в среде изменяются поля на тех же частотах (эффект самовоздействия), возникают новые поля на комбинационных частотах (эффект взаимодействия). Решая уравнение (2.8), найдём первое приближение поля . Затем берёт-
ся возмущение поля с точностью до второго порядка малости и ищется
второе приближение |
. Нелинейная часть уравнения будет зависеть от |
|||||||||
вычисленных поправок |
|
и |
. Таким образом, получаем цепочку не- |
|||||||
линейных уравнений |
|
|
|
|
|
|
0, |
|
|
|
|
|
|
|
|
|
4 |
|
|
||
|
|
|
̂ |
|
, |
|
||||
|
|
|
|
|
нл |
(2.9) |
||||
|
|
|
||||||||
|
|
|
̂ |
|
4 |
|
нл |
, |
|
|
|
|
|
|
|
||||||
… ,
где каждое последующее приближение вычисляется с помощью предыдущих. Процесс прекращается при достижении определённой точности приближения. Несмотря на удобство метода возмущений, он хорошо работает только тогда, когда поправки к нулевому приближению малы, т.е. возбуждаемые в среде волны малы по амплитуде по сравнению с амплитудами падающих волн, и можно ограничиться несколькими первыми приближениями. Поэтому метод возмущений в форме (2.2) практически не позволяет исследовать эффекты самовоздействия, процессы генерации гармоник при большой перекачке энергии и т.д. В этих и подобных им случаях применятся другой метод – метод медленно меняющихся амплитуд.
Метод медленно меняющихся амплитуд. Если среда является слабо нелинейной и слабо поглощающей, т.е. нл~ , , ~ , и на неё падают плоские монохроматические волны, то амплитуды волн будут изменяться на малую величину при прохождении волной расстояния
15

порядка длины волны, т.е. амплитуды волн будут медленно изменяющимся функциями координат. В соответствии с этим представим поле и поляризацию среды в виде
|
|
|
e |
, |
|
,волн, |
|
|
|
(2.10) |
|||
|
|
|
|
, |
|
|
|
|
(2.11) |
||||
где и |
– единичные векторы поляризацииe |
, |
и |
|
– медленно из- |
||||||||
меняющиеся амплитуды, |
– малый |
параметр, |
|
– |
|
волновой вектор |
|||||||
нелинейной поляризации на частоте |
, |
который в соответствии с частот- |
|||||||||||
ным соотношением (1.10) равен |
|
|
|
|
|
|
|
|
|
|
|
||
|
, |
, |
|
|
|
|
|
|
. |
|
|
|
(2.12) |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пусть нелинейная среда занимает полупространство |
|
|
|
, а векторы поля- |
|||||||||
ризации |
волн (в случае |
анизотропной |
среды) |
совпадают с векторами |
|||||||||
|
|
|
0 |
|
|||||||||
нормальных волн. Подставляя в уравнение Гельмгольца (1.27) выражения
(2.10) и (2.11), получаем
|
|
|
|
|
|
|
|
|
|
|
|
4 |
, . |
(2.13) |
|
|
|
|
|
|
|
|
|
|
|
||||||
Здесь мы учли, что |
|
|
|
|
|
, так как, мы |
|||||||||
|
|
|
|
|
|||||||||||
считаем, что волна распространяется в |
однородной среде вдоль оси . Про- |
||||||||||||||
|
|
– |
|
|
|
||||||||||
изводя дифференцирование в (2.13) и оставляя члены первого порядкаz |
|||||||||||||||
малости ( |
A |
|
0 , получаем |
|
4 |
|
, |
|
(2.14) |
||||||
Подставляя2 |
|
|
|
|
|
|
|
|
|
|
|
||||
в это уравнение выражение (2.12) |
и производя. |
необходимые |
|||||||||||||
преобразования, получаем систему укороченных уравнений для амплитуд, зависящих от пройденного расстояния z:
16

|
|
|
|
|
|
|
2 |
|
, |
, |
(2.15) |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
– коэффициент поглощения на частоте |
|
||||
где |
В правой/2части укороченных уравнений содержится осциллирующий. |
||||||||||
рактер |
exp |
, |
, который в сильной степени влияет на ха- |
||||||||
множитель |
|
||||||||||
|
|
|
|
|
|
|
|
||||
взаимодействия волн, так как он определяет знак работы внешней силы – волны нелинейной поляризации возбуждения поля. Наиболее эффективное взаимодействие будет осуществляться, если этот множитель равен единице, при этом величина работы имеет один знак на протяжении нелинейной среды. При условии
, |
(2.16) |
|
равна фазовой |
||
фазовая скорость электромагнитной волны на частоте |
скорости волны нелинейной поляризации на той же самой частоте, т.е. , . Соотношение (2.16) принято называть условием фазового синхро-
низма.
Если условие синхронизма заведомо не выполнено, то множитель
exp |
, |
сильно осциллирует и нелинейная поляризация слабо |
|
||
|
|
влияет на распространение волн: эффект взаимодействия может быть малым. В диспергирующей среде условию синхронизма (2.16) может удовлетворять лишь небольшое число волн, которые и участвуют во взаимодействии. Амплитуды остальных волн на комбинационных частотах настолько малы, что ими можно пренебречь.
Итак, задача о распространении волн в слабо нелинейных средах сводится к решению системы укороченных уравнений (2.15) для комплексных амплитуд волн, волновые векторы которых удовлетворяют или почти удовлетворяют условию фазового синхронизма (2.16).
17

Рассмотрим далее с помощью этого метода несколько основных задач из теории нелинейных волн по взаимодействию и самовоздействию.
3. Генерация второй гармоники
Пусть имеется среда, обладающая квадратичной нелинейностью, и на её границу падает плоская монохроматическая волна частоты . В такой среде возможен процесс генерации второй гармоники. Будем считать, что другими нелинейными эффектами (самовоздействием, генерацией высших гармоник, детектированием и т.д.) можно пренебречь. Тогда в среде рас-
пространяются |
только две волны |
на |
основной и |
удвоенной |
частотах: |
||||
гармоник, |
|
|
. При взаимодействии волн основной (первой) и второй |
||||||
в |
среде возбуждаются волны квадратичной поляризации на тех же |
||||||||
2 |
|
, |
|
|
|
|
|
||
частотах c |
волновыми векторами |
и амплитудами |
, равными (см. |
||||||
(1.12), (1.15) и (2.11)): |
, |
, |
|
, |
|
|
|||
|
|
|
2 |
|
|
(3.1) |
|||
|
|
|
1 |
|
|
,далее2 |
полагаются, |
(3.2) |
|
где единичные |
векторы поляризации, |
и |
равными |
||||||
2 |
|
|
|
и |
. Воспользуемся |
||||
единичным |
векторам взаимодействующих |
волн |
|||||||
укороченными уравнениями (2.15) с учётом выражений (3.1) и (3.2). При
этом предположим, что волны затухают слабо, |
|
(именно этот слу- |
|||||||||||
чай и представляет наибольший интерес), и |
пренебрежём членами |
. В |
|||||||||||
|
1 |
|
|
||||||||||
результате получаем систему укороченных уравнений |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
e |
, |
|
|
(3.3) |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
e |
, |
|
|
(3.4) |
|
|
|
|
|
|
|
|
|
|
||||
где малая расстройка волновых векторов равна |
|
|
|
||||||||||
2 |
|
2 |
|
, |
|
|
(3.5) |
||||||
|
|
|
|
|
18 |
|
|
|
|
|
|||

– показатель преломления,
2 ̂2 |
, |
2 ̂ |
. |
Умножим первое уравнение на , а во втором применим комплексное сопряжение к обеим частям, а потом умножим их на , затем сложим получившиеся выражения. Получим:
| | |
| | |
или |
. |
2 |
Когда отсутствует диссипация и нет притока энергии извне, должен выполняться закон сохранения общей энергии волны:
| |
| |
| |
| |
. |
(3.6) |
Видно, что при этом коэффициенты нелинейности равны друг другу:
Выявим основные закономерности. |
(3.7) |
генерации второй гармоники на |
основе решения укороченных уравнений (3.3) и (3.4). На входе в нелиней-
ную среду при |
0 зададим граничные условия: |
(3.8) |
||||
Строго говоря, |
0 |
, |
0 |
0. |
|
|
|
|
амплитуда второй гармоники на границе нелинейной среды |
||||
не равна нулю, но она имеет порядок |
, то0 |
0 |
так как мы считаем |
|||
среду слабо нелинейной, |
1 |
и можно положить |
||||
|
, и, |
|||||
0 |
0. |
|
|
|
|
|
Проанализируем сначала генерацию гармоники в условиях, когда её амплитуда мала по сравнению с амплитудой основной волны, | | | |. В этом случае можно пренебречь слабым обратным влиянием гармоники на основную волну, положив правую часть в (3.3) равной нулю. Тогда, очевидно, в рассматриваемом приближении амплитуда основной волны не
19
меняется, |
|
, и гармоника возбуждается в заданном поле основно- |
|||||||||||||
го излучения |
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(3.9) |
|||||
Интегрируя это уравнение, находим |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3.10) |
|
|
|
|
|
|
|
|
1 |
|
. |
|||||
Если |
0, т.е. выполняется условие фазового синхронизма |
(3.11) |
|||||||||||||
то, полагая в (3.9) |
|
|
, |
получаем, что амплитуда гармоники растёт пря- |
|||||||||||
|
|
2 , |
|
|
|
|
|
|
, |
|
|||||
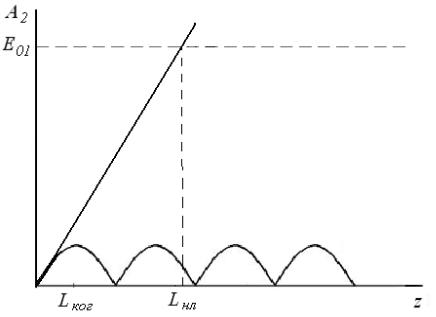
мо пропорционально |
пройденному расстоянию (рис. 1, кривая 1). |
|
|||||||||||||
0 |
|
| |
|
|
|
|
|
|
|
. |
|
||||
|
|
| |
|
|
|
|
|
|
|
(3.12) |
|||||
|
|
|
|
|
|
|
| |
| |
|
|
|
||||
В силу наложенного условия, |
|
|
, формула (3.12) справедлива до |
||||||||||||
длины |
нл, где |
|
|
|
|
нл |
|
. |
|
(3.13) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
На длине нл можно ожидать значительную перекачку энергии основной волны в энергию второй гармоники при фазовом синхронизме.
При рассогласовании фазовых
Рис. 1. Зависимость амплитуды второй гармоники| скоростей, , от расстояния в заданном поле основной волны
20
