
Исследование электрических колебаний методом фигур Лиссажу (90
..pdfФедеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Казанский национальный исследовательский технологический университет»
Исследование
электрических колебаний
методом фигур Лиссажу
Методические указания к лабораторным работам
Казань
КНИТУ
2 0 1 2
УДК 53(075.8)
Составители: доц. В.П.Архипов доц. Р.Х.Зиятдинов доц. О.И.Кондратьева асс. А.В.Репина
Исследование электрических колебаний методом фигур
Лиссажу: методические указания к лабораторным работам / В.П.Архипов [и др.].- Казань: Изд-во КНИТУ, 2012.- 21с.
Рассмотрены теоретические аспекты сложения электрических гармонических колебаний и образования фигур Лиссажу. Описана методика исследования процессов сложения электрических колебаний и наблюдения фигур Лиссажу при различных соотношениях частот и сдвигов фаз складываемых колебаний с помощью электронного осциллографа. Рассмотрены основные принципы измерения частоты колебаний путем сравнения с частотой эталонного генератора методом фигур Лиссажу.
Предназначены для студентов всех форм обучения, изучающих
раздел «Электричество и магнетизм» в рамках дисциплины «Физика».
Подготовлены на кафедре физики.
Печатаются по решению методической комиссии по циклу физико-математических дисциплин.
Рецензенты: доц. Мухтаров А.Ш. доц. Петухов Н.П.
2
ЛАБОРАТОРНАЯ РАБОТА № 242
ИЗУЧЕНИЕ ЭЛЕКТРИЧЕСКИХ КОЛЕБАНИЙ МЕТОДОМ ФИГУР ЛИССАЖУ
Цель работы: ознакомление с теорией сложения гармонических колебаний; изучение процессов сложения электрических колебаний путем наблюдения фигур Лиссажу на экране электронного осциллографа; определение частот и фазовых сдвигов колебаний с использованием эталонного генератора.
Приборы и принадлежности: электронный осциллограф С1-117/1, генератор сигналов низкочастотный Г3-112/1, генератор сигналов низкочастотный Г6-43, кабели и соединительные провода, разветвитель.
ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
1. Гармонические колебания.
Колебаниями называются процессы, в той или иной степени, повторяющиеся во времени. Колебательные процессы широко распространены в природе и технике, например, качание маятника, переменный электрический ток. При периодических колебаниях изменение наблюдаемой величины в точности повторяется через совершено определенное время –
период. Они описываются периодической функцией времени: f(t+nT)=f(t), (1)
где T – период функции, n – произвольное целое число. Колебание будет полным, если за кратчайшее время
система полностью повторит свое движение. Время Т, в течении которого совершается одно полное колебание, является периодом колебаний. Число полных колебаний в единицу времени называется частотой колебаний.
3
ν = |
1 |
, с-1 (Гц - герц) |
(2) |
|
|||
|
T |
|
|
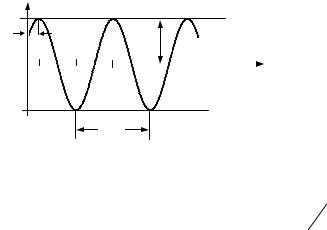
Среди разнообразных колебаний, встречающихся в природе, основную и очень важную роль играют гармонические колебания (рис.1).
ХХ=Аcos(ωt+φ0)
|
φ0 |
|
A |
(ωt+φ0),рад |
0 |
0 |
π |
||
|
2π |
|
t,c
Рис.1. ГармоническиеT колебания
Гармонические колебания представляют периодический процесс, в котором изменение наблюдаемой величины описывается функцией косинуса (или синуса):
x = A cos(ωt+ϕ ) или |
x = A sin(ωt+ϕ ) , |
ϕ =ϕ + π |
2 |
. (3) |
|
0 |
0 |
0 |
0 |
|
|
|
|
||||
Здесь x - отклонение (смещение) изменяющейся в процессе колебаний физической величины от положения равновесия. Наибольшее смещение A называется амплитудой колебаний.
Аргумент синуса или косинуса (ωt+ϕ0 ) определяет смещение в любой момент времени и называется фазой колебаний; ϕ0 -
начальная фаза (в момент времени t = 0). Величина ω , равная числу колебаний за 2π единиц времени, называется циклической (или круговой) частотой. Она в 2π раз больше обычной частоты ν :
ω=2πν или ω= |
2π |
, рад·с-1. |
(4) |
|
|||
|
T |
|
|
2.Вращающийся вектор амплитуды.
Если одна и та же материальная точка участвует в нескольких колебательных процессах одновременно, то её смещение в любой
4
момент времени можно найти геометрически методом вращающегося вектора амплитуды (методом векторных диаграмм).
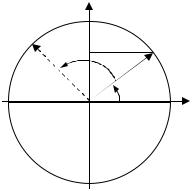
Изобразим на координатной плоскости ХОY вектор A с началом в точке О (рис.2). Длина вектора равна амплитуде
колебаний. Угол, образуемый вектором A с осью ОХ, равен начальной фазе колебания ϕ0 . Если привести вектор A во вращение вокруг начала координат О с частотой, равной циклической частоте колебания ω , то его проекции на координатные оси OX и OY будут изменяться по
гармоническому закону: |
(5) |
x = A cos(ωt+ϕ0 ) y = A sin(ωt+ϕ0 ) |
Y
ωt A
ϕ0  Х
Х
О
Рис.2. Проекции вектора A на координатные оси совершают
гармонические колебания: а) амплитуда колебаний равна длине вектора A , б) круговая частота равна угловой скорости его вращения, в) начальная фаза
колебания ϕ0 равна углу, образуемому вектором A с осью ОХ в начальный момент времени, г) фаза колебания в произвольный момент времени равна
ωt+ϕ0
Рассмотрим некоторые частные случаи сложения гармонических колебаний.
5
3.Сложение гармонических колебаний одного направления.
Пусть два гармонических колебания происходят в одном направлении ОХ, имеют одинаковые частоты ω1 = ω2 = ω, но различные начальные фазы j1 ¹ j2 . Запишем уравнения этих колебаний:
x1=A1cos(ωt+j1 ) |
и x2 =A2cos(ωt+j2 ) . |
(6) |
Результирующее смещение точки равно: |
|
|
x = x1 + x2 = A cos(wt + j). |
(7) |
|
Амплитуду и начальную фазу ( A,j ) результирующего колебания найдем методом векторных диаграмм (метод вращающегося вектора амплитуды).
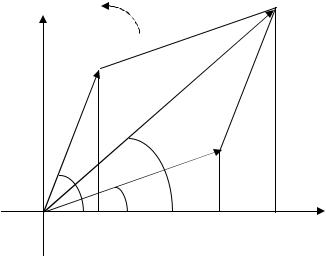
Результирующее смещение x = x1 + x2 легко можно найти графически, изобразив на координатнойr r плоскости два вращающихся вектора амплитуд A1,A2 , рис.3. Углы,
образуемые этими векторами с осью ОХ в начальный момент
времени |
r |
j1 |
иj2 |
равны начальным фазамколебаний. Так как |
|
|
r |
|
|
вектора A1 |
и A2 |
вращаются вокруг начала координат с |
||
одинаковой угловой скоростью ω , равной круговой частоте колебаний, то угол между ними не меняется со временем и
|
|
|
r |
Y |
|
|
A |
ω |
|
|
|
|
|
|
|
|
r |
|
|
|
A1 |
|
|
|
j |
|
r |
|
j1 |
|
A2 |
|
|
|
|
|
j2 |
|
Х |
|
|
|
|
О |
x |
x2 |
x |
|
1 |
|
|
Рис.3. Сложение гармонических колебаний одного направления и одинаковой частоты графическим методом
6

равен ϕ = ϕ1 − ϕ2 .
Как следует из рис.3, амплитуда результирующего колебания
(длина вектора A ) равна:
A = A |
2 |
+ A |
2 |
+ 2A |
A |
2 |
cos(ϕ − ϕ |
) , |
(8) |
|
|
1 |
|
2 |
1 |
|
1 |
2 |
|
|
|
а начальная фаза определяется соотношением:
ϕ = arc tg |
A1 sinϕ1 |
+ A2 |
sinϕ2 |
. |
(9) |
|||
|
|
|
||||||
|
A |
cos ϕ |
+ A |
2 |
cos ϕ |
2 |
|
|
1 |
1 |
|
|
|
|
|||
Если разность фаз колебаний равна четному числу полуоборотов, или другими словами четному числу π радиан, то есть:
ϕ1 − ϕ2 = 2k π, |
(10) |
то амплитуда результирующего колебания будет максимальной:
A = A1 + A2 . |
(11) |
Если разность фаз колебаний равна нечетному числу полуоборотов, или другими словами нечетному числу π радиан, то есть:
ϕ1 − ϕ2 = (2k +1)π, |
(12) |
то амплитуда результирующего колебания будет минимальной:
A = A1 − A2 . |
(13) |
4.Сложение взаимно перпендикулярных гармонических колебаний одинаковой частоты
Два гармонических колебания с одинаковыми частотами
происходят во взаимно перпендикулярных направлениях (по осям ОХ и ОY):
x = A1cos(ωt+ϕ1 ) и y = A2cos(ωt+ϕ2 ) |
(14) |
В зависимости от соотношения амплитуд A1 , A2 и начальных
7
фаз j1 , j2 складываемых колебаний точка будет двигаться или
по эллипсу или по окружности или по прямым линиям (в 1,3 или 2,4 четвертях).
А) Пусть A1 ¹ A2 и разность фаз Dj = j1 - j2 = ± p2 , тогда:
x = A1cosωt
y = A2cos(ωt
Возводим уравнения в
|
|
|
x |
=cosωt |
|
|
|
|
|||
|
|
|
|
||
|
|
A1 |
|||
± p ) |
|
|
y |
=± sinωt |
|
|
|
||||
2 |
|
|
A2 |
||
|
|
||||
квадрат и исключаем время:
|
x |
2 |
|
y |
2 |
||
|
|
+ |
|
=1 |
|||
A1 |
A2 |
||||||
|
|
|
|
|
|||
(15)
(16)
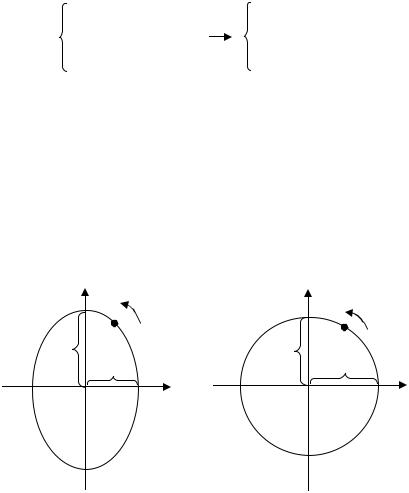
Полученное уравнение или траектория движения точки является эллипсом с полуосями A1 и A2 . Если A1 = A2 , то эллипс
превращается в окружность. Таким образом, результирующее движение точки – это движение с постоянной угловой скоростью ω по эллипсу с полуосями A1 и A2 (рис.4а) или по
окружности с радиусом A = A1 = A2 (рис.4б).
Y |
|
Y |
|
ω |
ω |
A2 |
A1 |
A |
|
A |
|
|
X |
X |
а |
б |
|
Рис.4. Траектория точки, участвующей в двух взаимно |
||
перпендикулярных колебаниях одинаковой частоты и |
разностью фаз |
|
Δϕ = ± π : а) амплитуды колебаний |
различны A2 > A1 , |
б) амплитуды |
2 |
|
|
колебаний одинаковы A2 = A1 .
8
Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»
Б) Пусть A1 ¹ A2 и разность фаз Dj = j1 - j2 |
= 0 , тогда: |
||||||||||||||||||
|
x = A1cosωt |
|
|
x |
= |
A1 |
|
|
|
|
|
(17) |
|||||||
|
|
|
|
|
|
||||||||||||||
|
y = A2cosωt |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
y A2 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
Уравнение |
y = |
A1 |
x |
является |
|
уравнением |
прямой |
линии, |
|||||||||||
|
|||||||||||||||||||
|
|
A2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
находящейся в 1,3 четвертях координатной плоскости XOY, |
|||||||||||||||||||
рис.5. |
¹ A2 и разность фаз Dj = j1 - j2 = p , тогда: |
|
|||||||||||||||||
Пусть A1 |
|
||||||||||||||||||
x = A1cosωt |
|
|
x=A1cosωt |
|
|
x |
=- |
A1 |
|
(18) |
|||||||||
|
|
|
|||||||||||||||||
|
|||||||||||||||||||
y = A2cos(ωt+p) |
|
|
y =- A2cosωt |
|
|
y |
|
A2 |
|
||||||||||
|
|
|
|
|
|||||||||||||||
Полученное уравнение является уравнением прямой линии, находящейся во 2,4 четвертях координатной плоскости, рис.5.
Результирующее движение точки является гармоническим
колебанием вдоль прямой y = |
A1 |
x |
или |
y = - |
A1 |
x с частотой |
||||||
|
|
|||||||||||
|
|
A2 |
|
|
|
|
|
|
A2 |
|||
ω и амплитудой A = |
A12 + A22 . |
|
|
|
|
|
|
|
|
|||
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
а |
|
|
|
y = |
A1 |
x |
|
|
|
||
2 |
|
|
|
A2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
б |
A1 |
|
|
|
|
|
|
|
|
|
|
|
X |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
y = − |
A1 |
x |
|
|
|||
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
A2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.5. Траектория движения точки, участвующей в двух взаимно перпендикулярных колебаниях одинаковой частоты, произвольной амплитуды A2 ¹ A1 : а) разность фаз Dj = 0 , б) разность фаз Dj = p .
9
5.Сложение взаимно перпендикулярных гармонических колебаний с кратными частотами
Пусть точка совершает одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях, но с различными частотами ω1 ¹ ω2 . Если частоты или периодыT1,T2
этих колебаний относятся как целые числа:
|
T1 |
= |
n |
, (n,m - целые числа), |
(19) |
|
T2 |
|
|||
|
|
m |
|
||
то через промежуток времени, равный наименьшему общему |
|
||||
кратному обоих периодов, движущаяся точка снова |
|
||||
возвращается в начальное положение. (Наименьшее общее |
|
||||
кратное двух целых чисел m , n – наименьшее натуральное |
|
||||
число, которое делится без остатка на каждое из этих двух |
|
||||
чисел.) |
|
|
|
|
|
Траектория точки представляет сложную петлеобразную кривую. В общем случае вид траекторий зависит от соотношения между частотами, фазами и амплитудами колебаний. Впервые они были изучены французским ученым Ж. Лиссажу* и называются фигурами Лиссажу.
Если частоты обоих колебаний существенно отличаются друг от друга, то фигуры Лиссажу не наблюдаются.
Ниже на рис.6 приведены фигуры Лиссажу для некоторых не очень сложных случаев, отличающихся разностью фаз и соотношением частот колебаний. Рассмотренные выше варианты сложения взаимно перпендикулярных колебаний при равенстве их
частот представляют самый простой вид фигур Лиссажу.
----------------------------------------------------------------------------------------
* Лиссажу Жуль Антуан (1822-1880) – французский физик. Работы посвящены акустике и оптике. Разработал (1855)
10
