Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Аналитическое решение задач оптимального проектирования элементов несущих конструкций (120

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

300.11 Кб

Скачать

☆

<<< < Предыдущая 1 2 34 / 44

ления нагрузки, если задана масса, и для определения массы, если задана нагрузка;

4)определить оптимальные параметры проектируемого стержня по зависимостям, приведенным в подразд. 1.3;

5)рассчитать предельные значения нагрузок: по прочности — по формуле (39), общей устойчивости — по формуле (40), по местной устойчивости — по формуле (41). Сделать вывод о несущей способности спроектированной конструкции.

3.ПРИМЕРЫ ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ

3.1. Задача оптимального проектирования стержня из изотропного материала

при наличии ограничений

Исходные данные. Определить оптимальные параметры цилиндрического тонкостенного стержня длиной L = 1,4 м, предназначенного для восприятия сжимающей нагрузки P = 15 кН. Свойства материала: модуль упругости E = 70 ГПа, предельное напряжение при сжатии [σ] = 160 МПа, плотность ρ = 2800 кг/м3. Минимальная толщина hmin = 0,5 мм, максимальный радиус Rmax = 40 мм. Коэффициент устойчивости k = 0,2.

Ход и результаты решения. Задача оптимизации является двухмерной; искомые варьируемые параметры: толщина h и радиус R стержня;

Eσ

3,14

2 ·70 · 10· 9

= 0,0301 м = 30,1 мм.

]

1,4

160

106

образом, R

2[σ]

;

Таким

max

2πk

·70 · 10· 9

2[σ]

3(1

−

ν2)

L =

160 106

·3(1,14− 00,,322)

· 1,4 = 5,69 · 10−4 м = 0,569 мм.

min

2πk

Таким образом, h

2[σ]

3(1 − ν2)

Итак, решаемая задача является задачей второго типа;

	3) G						= ρ							3(1 −							ν2)						1	=								1
	3) G						= ρ							3(1 −							ν2)							=								1
				(2)						16				πkL5hmin4													3

= 2800 ·																						5											4		4	3			= 0,355 кг;
= 2800 ·						16 · 3,14 · 03,2												(1· 1,4						0·,325)· 10−															= 0,355 кг;


															·						−														2 L3
																																							ρ
																			4					(1						2)		[
												G =								3 πk− ν												[	σ]							=
												G =								3 πk− ν														E2						=
																														6	2					3
																	2													6	2					3
			4 ·									3,14 · 0,2 · (70 · 10 )																					· 1,4					· 2800
		=																																								= 0,422 кг;
																														9		2
		(2)		=				2πkEh2													2			·	3,14				·	0,2					70			109			5		·	10−4	2	=
	P			=					3(1 −					ν2) =										·					·				3·		· (1·− 0,3·						2)		·			=
														min
= 13300					Н = 13,3 кН;
= 13300
																					3			2
	P = 4 3														2	)					3			2			=
	P = 4 3									πk− ν						)		[σE] 2									=
										(1												L
																											6	3					2
													2							·							6	3					2
				3 ·		3 14 · 0 2 ·									·					·									· 1,4
=	4 ·			3 ·			(1 − 0,3							)	·			160 · 10											· 1,4						= 172000 Н = 17,2 кН.
								,				,			(70									9		2
								,				,			(70						10 )
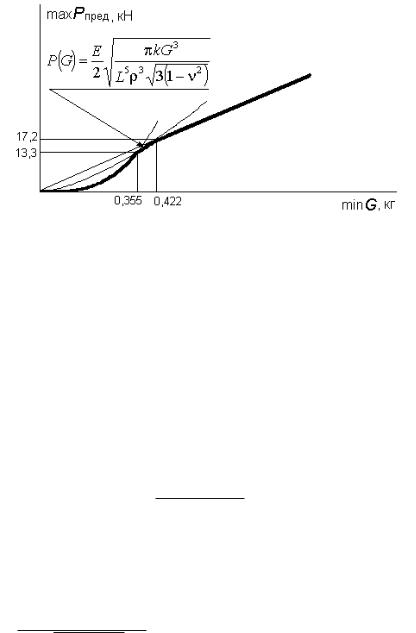
	Граница предельных возможностей проектируемой конструк-
ции показана на рис. 22;
	4) для заданного участка справедливо равенство
	G = 4P2L5ρπkE32(1 −																											1		=
	G = 4P2L5ρπkE32(1 −																							ν2)						=
													3															3
=		4 · 150003,·14												0,·2					(70				·109)2							−									1
=		4 · 150003,·14												0,·2					(70				·109)2							−							= 0,385 кг;
									2			·		5			·				3	·													2				3
										1,4						2800											3(1					0,3 )
	5) oптимальные параметры проектируемого стержня:
	h = 2									πkL5					ρ−3			ν						1		=
				1			G3				3(1									2)				4
32

Рис. 22. Граница предельных возможностей

= 2

3,14

0·,2 1·,45

−28003

м = 0,531 мм;

= 5,31 · 10−4

0,385

0,3 )

R =

0,385

2πLρ

2 · 3,14 · 1,4 · 2800 · 5,31 · 10−4

= 0,0295 м = 29,5 мм.

Полученное решение единственное;

6) предельная нагрузка по прочности

Pпр = 2π[σ]Rh = 2 · 3,14 · 160 · 106 · 0,0295 · 5,31 · 10–4 =

= 15700 Н = 15,7 кН; предельная нагрузка по общей (стержневой) устойчивости

Pуст(об) =	π3E	R3h =	3,143 · 70 · 109	·	0,02953	·	5,31	·	10−4	=
	L2
			1,42

= 15000 Н = 15,0 кН;

предельная нагрузка по местной (оболочечной) устойчивости

(м)		2πkE
Pуст	=		h2 =

		3(1 − ν2)

= 2 · 3,14 · 0,2 · 70 · 109 · 5,31 · 10−4 2 = 15000 Н = 15,0 кН.

3(1 − 0,32)

Несущая способность оптимальной конструкции определяется равноустойчивостью; по прочности имеется дополнительный запас.

3.2. Задача оптимального проектирования композитного стержня

с ортогонально армированной структурой

Исходные данные. Определить оптимальные параметры цилиндрического тонкостенного стержня длиной L = 1,4 м, предназначенного для восприятия сжимающей нагрузки P = 50 кН. Свойства однонаправленного материала: модуль упругости вдоль волокон E1 = 240 ГПа, предельное напряжение при сжатии вдоль волокон [σ] = 580 МПа, плотность ρ = 1500 кг/м3. Слои материала ориентированы вдоль оси стержня и в кольцевом направлении Коэффициент устойчивости k = 0,2.

Ход и результаты решения. Задача оптимизации является трехмерной; искомые варьируемые параметры: толщина h и радиус R стержня, а также относительная доля продольных слоев в

структуре композита ˜ ; h0

			12			F		−			2 L3ρ
							π			1
	1) G =						1								=
	1) G =							kE2							=
					6		2				·	3
	3 14 · 0 2 ·										·		· 1500
=	12 · 580	·		10					· 1,4				· 1500					= 0,459						кг;
,				, (240									9		2
,				, (240								10		)
9			F−			3 L2							9			580					106		3		1,42
				1			1				=		3 14				0 2							·	9 2 = 95100 Н =
	P =			1			2				=			,	·		,		·			(240		·	9 2 = 95100 Н =
			πkE											,	·		,			·		(240		·	10 )
= 95,1 кН.															·					·				·
= 95,1 кН.

Таким образом, P < P ;

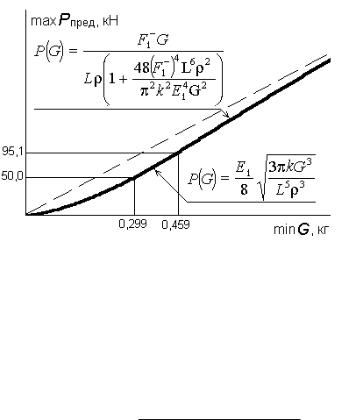
2)граница предельных возможностей проектируемой конструкции показана на рис. 23;

3)нагрузка и масса на первом участке связаны зависимостью

P = 81				L5ρ3	,
	E			3πkG3

Рис. 23. Граница предельных возможностей

откуда

					1	= 4														1
G = 4	3			πkEρ2	1				3 · 3,14 · 0·,2 · (240· · 109)2												=0,299 кг;
G = 4	3			πkEρ2					3 · 3,14 · 0·,2 · (240· · 109)2												=0,299 кг;
	P			2L5 3	3					500002				1,45			15003			3
4) oптимальные параметры:
				G3		1									,2993						1
				G3		4									,2993						4
h =		3				=								30·,02							=
h =		16πkL5ρ3				=				16	·	3,14		30·,02		·	1,45	·	15003		=
= 8,14 · 10–4 м = 0,814 мм;											·			·		·		·
= 8,14 · 10–4 м = 0,814 мм;
R =					1		3		3·,143			·	1500		1	= 0,0279 м = 27,9 мм.
R =			3π3ρ =				3		3·,143			·	1500			= 0,0279 м = 27,9 мм.
			kLG		4		0,2			1,4			0,299		4
								·		˜		·			˜
Структурные параметры: h0												= 0,75, h90 = 0,25.

Полученное решение единственное.

Проверка: масса G = 2πLρRh = 2 · 3,14 · 1,4 · 1500 · 0,0279 ×

×8,14 · 10–4 = 0,299 кг;

5)предельная нагрузка по прочности

Pпр = 2

πF−Rhh˜

= 2

3,14

580

106

0,0279

8,14

10–4

0,75 =

= 61800 Н

= 61,8

кН;

предельная нагрузка по общей (стержневой) устойчивости

	3		3	˜
Pуст(об)	=	π	E1R hh0		=
			L2

= 3,143 · 240 · 109 · 0,02793 · 8,14 · 10−4 · 0,75 =50000 Н =50,0 кН; 1,42

предельная нагрузка по местной (оболочечной) устойчивости

2πkE

h˜0

1 − h˜0

Pуст( ) =

√

3,14

0,2

240

109

(8,14

10−4)2

√·

0,75 · (1 − 0,75) =

= 50000 Н = 50,0 кН.

ЛИТЕРАТУРА

1.Смердов А.А. Основы оптимального проектирования композитных конструкций М.: Изд-во МГТУ им. Н.Э. Баумана, 2006. 88 с.

2.Балабух Л.И., Алфутов Н.А., Усюкин В.И. Строительная механика ракет: учеб. пособие. М.: Высш. шк., 1984. 391 с.

ОГЛАВЛЕНИЕ
Вводная часть . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	3
1. Вывод расчетных зависимостей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	4
1.1. Основные подходы к оптимальному проектированию
конструкции, понятия и определения . . . . . . . . . . . . . . . . . . . . .	4
1.2. Задача оптимального проектирования стержня из
изотропного материала при наличии ограничений . . . . . . . .	7
1.3. Задача оптимального проектирования композитного стержня
с ортогонально армированной структурой . . . . . . . . . . . . . . . .	21
2. Методика выполнения домашнего задания . . . . . . . . . . . . . . . . . . . . .	28
2.1. Задача оптимального проектирования стержня из
изотропного материала при наличии ограничений . . . . . . . .	28
2.2. Задача оптимального проектирования композитного стержня
с ортогонально армированной структурой . . . . . . . . . . . . . . .	30
3. Примеры выполнения домашнего задания . . . . . . . . . . . . . . . . . . . . .	31
3.1. Задача оптимального проектирования стержня из
изотропного материала при наличии ограничений . . . . . . . .	31
3.2. Задача оптимального проектирования композитного стержня
с ортогонально армированной структурой . . . . . . . . . . . . . . . .	34
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	37

Учебное издание

Смердов Андрей Анатольевич

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ ЭЛЕМЕНТОВ НЕСУЩИХ КОНСТРУКЦИЙ

Редактор О.М. Королева Корректор Е.В. Авалова

Компьютерная верстка В.И. Товстоног

Подписано в печать 11.07.2011. Формат 60×84/16. Усл. печ. л. 2,33. Тираж 100 экз. Изд. № 76.

Заказ

Издательство МГТУ им. Н.Э. Баумана. Типография МГТУ им. Н.Э. Баумана. 105005, Москва, 2-я Бауманская ул., 5.

ДЛЯ ЗАМЕТОК

<<< < Предыдущая 1 2 34 / 44

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.2022556.32 Кб4Анализ хозяйственной деятельности (90..pdf
#
15.11.2022426.46 Кб6Анализ хозяйственной деятельности предприятий Учебно-методическое пособие к курсовой работе для бакалавров направления 38.03.01 Экономика.pdf
#
15.11.2022617.24 Кб13Аналитическая механика (90..pdf
#
15.11.2022811.08 Кб10Аналитическая химия. Осадительное титрование методические указания.pdf
#
15.11.2022608.6 Кб6Аналитический инструментарий журналиста (110..pdf
#
15.11.2022300.11 Кб19Аналитическое решение задач оптимального проектирования элементов несущих конструкций (120..pdf
#
15.11.2022737.82 Кб10Аналоговая и цифровая фильтрация сигналов (110..pdf
#
15.11.20221.28 Mб15Аналоговые электронные элементы (96..pdf
#
15.11.20223.77 Mб13Анатомический практикум. Строение и функция двигательных черепных нервов Учебное пособие.pdf
#
15.11.20222.96 Mб19Анатомический практикум. Черепные нервы специальной чувствительности Учебное пособие.pdf
#
15.11.2022113.99 Кб5Анатомия животных. Аппарат движения и общий покров в 5 частях.pdf