Аналитическое решение задач оптимального проектирования элементов несущих конструкций (120

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Московский государственный технический университет имени Н.Э. Баумана

А.А. Смердов

АНАЛИТИЧЕСКОЕ РЕШЕНИЕ ЗАДАЧ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ ЭЛЕМЕНТОВ НЕСУЩИХ КОНСТРУКЦИЙ

Методические указания к выполнению домашнего задания

Москва Издательство МГТУ им. Н.Э. Баумана

2011

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

УДК 624.04 ББК 38.112 С50

Рецензент Б.С. Сарбаев

Смердов А.А.

С50 Аналитическое решение задач оптимального проектирования элементов несущих конструкций: метод. указания к выполнению домашнего задания / А.А. Смердов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2011. – 35, [5] с. : ил.

Рассмотрено аналитическое решение задач оптимального проектирования элементов несущих конструкций в виде сжатых стержней.

Для студентов 5-го и 6-го курсов факультета «Специальное машиностроение».

Рекомендовано учебно-методической комиссией факультета СМ МГТУ им. Н.Э. Баумана.

УДК 624.04 ББК 38.112

c МГТУ им. Н.Э. Баумана, 2011

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

ВВОДНАЯ ЧАСТЬ

Целью настоящего домашнего задания является отработка навыков аналитического решения задач оптимального проектирования элементов несущих конструкций.

Впроцессе выполнения домашнего задания и подготовки его

кзащите необходимо усвоить такие основные понятия, как скалярная и векторная оптимизация, варьируемые параметры, диапазоны варьирования, целевая функция, функциональные ограничения, минимизация массы, максимизация несущей способности, границы предельных возможностей, а также научиться ставить и решать задачи исследования предельных возможностей несущих конструкций, к которым предъявляются требования минимальной массы и максимальной несущей способности [1].

Задание заключается в выборе оптимальных параметров стержней, предназначенных для восприятия сжимающих нагрузок.

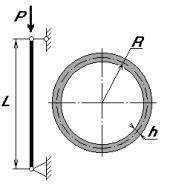
Схема объекта оптимизации показана на рис. 1. Стержень длиной L выполнен в виде тонкостенной трубы и закреплен по торцам (при решении могут быть приняты граничные условия свободного опирания). Конструкция нагружена осевой сжимающей силой P. Считается, что заданное значение P соответствует расчет-

ной нагрузке, определенной с учетом Рис. 1. Объект оптимизации коэффициента безопасности [2].

Целью проектирования является выбор параметров, соответствующих минимальной массе при заданной несущей способности

3

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

конструкции или максимальной несущей способности при заданной массе.

В домашнем задании предусмотрено решение задач двух типов:

1)задачи оптимального проектирования стержня из изотропного материала при наличии ограничений на варьируемые параметры;

2)задачи оптимального проектирования композитного стержня

сортогонально армированной структурой.

Каждая из этих задач имеет свою методику решения, однако обе они основаны на общем подходе, который рассмотрен в разд. 1. Там приведены определения и понятия, а также вывод соотношений, необходимых для выполнения домашнего задания.

Предлагаемый материал изучается в лекционных курсах (в частности, приведен в учебном пособии [1]).

Вразд. 2 описана методика выполнения и оформления задания,

ав разд. 3 приведены примеры выполнения домашнего задания.

1.ВЫВОД РАСЧЕТНЫХ ЗАВИСИМОСТЕЙ

1.1.Основные подходы к оптимальному проектированию конструкции, понятия и определения

При формулировке задачи оптимального проектирования необходимо выбрать:

1)объект оптимизации;

2)варьируемые параметры;

3)критерии качества.

Выбор объекта оптимизации предполагает: выделение объекта как подсистемы некоторой более общей системы с установлением связей между ними; выбор конструктивной схемы или круга конструктивных схем; выбор используемых материалов (или ограничение круга потенциально возможных материалов); построение математической модели оптимизируемого объекта.

Варьируемые параметры — это те параметры, которые могут быть изменены в соответствии с выбранным алгоритмом оптимизации. Параметры, которые должны сохранять постоянные значения, именуются директивными. Варьируемые параметры обычно

4

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

представляются в виде вектора X = {x1,x2,...,xn}. Число независимых варьируемых параметров n называется размерностью задачи оптимизации. Как правило, при выборе варьируемых параметров следует указать диапазоны варьирования, т. е. наименьшие и наибольшие допустимые значения каждого параметра ximin и

ximax.

Критерии качества — это требования к свойствам проектируемой конструкции. Каждое отдельное требование к какому-либо свойству принято называть локальным критерием эффективности

(ЛКЭ). Каждый ЛКЭ может быть представлен в виде функции от вектора варьируемых параметров.

Все ЛКЭ могут быть подразделены на два класса:

1)экстремальные критерии (требования максимума или минимума данной характеристики);

2)критерии в виде ограничений (требования нахождения ха-

рактеристик в заданных пределах, обычно формулируемые в виде неравенств).

В зависимости от того, как сформулированы ЛКЭ, задачи оптимального проектирования можно подразделить на несколько типов.

Если среди всех ЛКЭ есть только один экстремальный критерий, а все остальные требования сформулированы как ограничения, то имеет место задача скалярной оптимизации. Количество ограничений в скалярной задаче может быть любым. Если экстремальных критериев больше одного, то это задача векторной оптимизации. В ней также может присутствовать любое количество ограничений на свойства проектируемой конструкции.

Задача скалярной оптимизации называется также задачей математического программирования (МП). В ней вектору варьируемых параметров соответствует так называемая целевая функция M(X), представляющая собой математическую запись единственного экстремального ЛКЭ. Кроме того, возможно произвольное количество функций-ограничений, для каждой из которых также установлены границы допустимых диапазонов значений. Задача МП формулируется следующим образом: необходимо отыскать такое значение X , при котором целевая функция принимала бы наибольшее или наименьшее среди всех возможных значений, а все ограничения были бы выполнены. Область значений вектора X, в которой выполняются все ограничения, называется областью допустимых решений Dx.

5

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Наиболее важный класс задач векторной оптимизации — задачи исследования предельных возможностей, в которых изменяются не только варьируемые параметры, но и требования к свойствам проектируемого изделия.

При векторной оптимизации также выделяется вектор варьируемых параметров X, для которого формулируются диапазоны варьирования. Однако теперь этому вектору ставится в соответствие не одна скалярная функция, а вектор эффективности

Y(X) = {y1(X),y2(X),...,yk(X)}. Компоненты этого вектора — требования к свойствам конструкции, причем каждое требование

предполагает поиск максимума или минимума. В векторной задаче также может присутствовать любое количество ограничений.

Основной подход к решению задачи векторной оптимизации связан с выделением не одного решения, а множества оптимальных реализаций проекта. Этот подход носит название оптимизации по Парето, а множество полученных оптимальных решений называют

областью компромиссов или областью Парето.

Область компромиссов определяется как такое подмножество множества допустимых решений Dx, в котором ни один из входящих в него проектов не может быть улучшен по всем критериям сразу. Это значит, что для любых двух точек этого множества X и X всегда можно указать критерий yi(X), значение которого лучше в точке X , и всегда можно указать критерий yj(X), значение которого лучше в точке X . На основе анализа области компромиссов принимается решение о выборе параметров того или иного конкретного проекта.

Для построения области компромиссов необходимо перебрать все возможные реализации данного проекта и путем непосредственного сравнения выяснить, какие из них входят в эту область, а какие нет. Поскольку в реальных задачах это, как правило, невозможно (исключением являются одномерные задачи оптимизации, которые могут быть исследованы методами параметрического анализа), для проектируемых конструкций могут быть построены

границы предельных возможностей.

Граница предельных возможностей строится в пространстве требований к свойствам проектируемой конструкции. Для ее построения сначала из вектора Y(X) выбирается один критерий yi(X). Для этого критерия ставится и решается цикл задач ска-

6

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

лярной оптимизации, в которых сам он выступает в качестве целевой функции, а все остальные компоненты вектора Y(X) — в качестве ограничений. Уровни ограничений в каждой скалярной задаче выбираются разными:

где k — номер текущей задачи скалярной оптимизации. Величины

A(jk) изменяются в пределах всего интересующего проектанта диапазона; при этом строится зависимость полученных оптимальных

значений yi от A(jk). Затем, если это необходимо, возможен выбор другого критерия yk(X) в качестве целевой функции и повторение описанной процедуры. Решение скалярных задач продолжается до тех пор, пока не будет окончательно определен вид границы предельных возможностей.

Полученная граница отделяет область доступных сочетаний требований к свойствам проектируемой конструкции от области невозможного при проектировании с данными директивными параметрами. Исследование участков этой границы, соответствующих проектам конструкций с точно заданными значениями характеристик, позволяет выявить оптимальные значения варьируемых параметров для каждого такого проекта. Примеры такого исследования приводятся ниже.

Более подробно представленные здесь подходы, понятия и определения охарактеризованы в учебном пособии [1].

1.2. Задача оптимального проектирования стержня из изотропного материала

при наличии ограничений

Объект оптимизации изображен на рис. 1 и представляет собой прямолинейный стержень длиной L c тонкостенным трубчатым сечением, нагруженный осевой сжимающей силой P. Стержень выполнен из однородного изотропного линейно-упругого материала. Граничные условия на торцах стержня соответствуют шарнирному опиранию (несложно рассмотреть аналогичную задачу и при других вариантах граничных условий).

7

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Варьируемыми параметрами являются радиус стержня R и

толщина стенки h:

следует, что можно не учитывать различия между средним, внешним и внутренним радиусами. Границы диапазонов варьирования вводятся соотношениями

Здесь учтены два наиболее типичных ограничения: на минимальную толщину и на максимальный радиус. Первое из них определяется возможностями изготовления и эксплуатации стержня, второе — конструктивными требованиями к компоновке окружающего пространства. При любых изменениях параметров должно выполняться соотношение (3).

Директивными параметрами являются длина L, свойства материала стержня (модуль упругости E, коэффициент Пуассона ν, предельное напряжение при сжатии [ σ] и плотность материала ρ), а также величины Rmax и hmin и коэффициент устойчивости k [2].

Критериями качества в данной задаче являются масса стержня G и предельно допустимая нагрузка Pпред (отношение Pпред/P составляет запас по несущей способности конструкции). Масса должна быть минимизирована, а предельная нагрузка — максимизирована. Таким образом, имеет место задача векторной оптимизации:

Масса стержня может быть выражена через варьируемые параметры простой формулой:

Несущая способность конструкции может определяться тремя различными механизмами: прочностью, общей устойчивостью (устойчивостью стержня) и местной устойчивостью (устойчивостью конструкции как тонкостенной цилиндрической оболочки).

8

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Каждому из них соответствует свое значение предельной нагрузки. При возрастании нагрузки P конструкция разрушится по тому механизму, которому соответствует наименьшее из этих значений. Таким образом, максимизация несущей способности представляет собой максимизацию наименьшей из трех функций:

maxPпред (X) = max min Pпр (X), Pуст(об) (X),Pуст(м) (X) . (7)

X Dx

Предельная нагрузка по прочности конструкции представляет собой произведение предельного напряжения при сжатии и площади поперечного сечения:

Предельная нагрузка по общей (стержневой) устойчивости определяется формулой Эйлера [2]

предельная нагрузка по местной (оболочечной) устойчивости для изотропной цилиндрической оболочки [2] — по формуле

Решение задачи векторной оптимизации проводится в соответствии с методикой, описанной в подразд. 1.1. Выбирается один из критериев качества — несущая способность — и решается вспомогательная скалярная задача (1):

где допустимое значение ограничения G — переменная величина. Еще более упрощается вспомогательная задача при допущении о том, что ограничение (11) для оптимальных проектов всегда должно выполняться в виде равенства (справедливость этого утверждения проверяется по ходу решения). Таким образом, вспо-

могательная задача формулируется следующим образом:

max min Pпр (X), Pуст(об) (X), Pуст(м) (X) при G(X) = const.

(12)

9

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Условие G(X) = const связывает варьируемые параметры, так что один из них можно выразить через другой:

Подставив (13) в формулы (8)—(10), можно получить выражения для составляющих несущей способности стержня фиксированной массы:

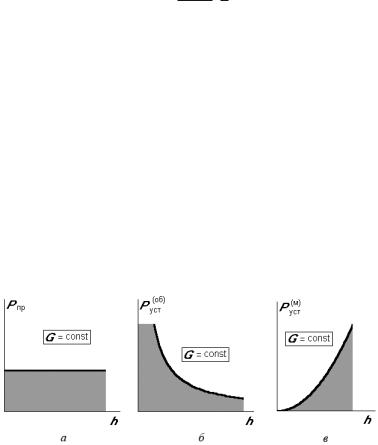
Зависимости (14) изображены на рис. 2. На рис. 2, а показано условие прочности; зона прочности выделена затемнением. Так же затемнением на рис. 2, б показана зона общей устойчивости, а на рис. 2, г — зона местной устойчивости.

Рис. 2. Границы зон прочности (а), общей (б) и местной (в) устойчивости для стержня фиксированной массы

Теперь нужно совместить графики и отыскать максимум несущей способности в зоне, где все три затемненные зоны совпадают. Однако совмещать эти графики следует не во всем первом квадранте плоскости варьируемых параметров, а только лишь в области допустимых решений Dx, которая в данном случае определяется

10