Аналитическое решение задач оптимального проектирования элементов несущих конструкций (120

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Критическим значениям массы соответствуют нагрузка (27) и нагрузка

1.3. Задача оптимального проектирования композитного стержня

с ортогонально армированной структурой

Аналитические решения задач оптимизации композитов с варьируемой структурой встречаются чрезвычайно редко. Тем не менее при некоторых упрощающих допущениях удается сформулировать и решить задачу оптимального проектирования композитного стержня из ортогонально армированного волокнистого материала.

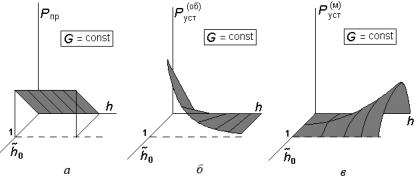
Объект оптимизации (cм. рис. 1) представляет собой прямолинейный стержень длиной L c тонкостенным трубчатым сечением, шарнирно опертый по торцам и нагруженный осевой сжимающей силой P.

Общая схема объекта оптимизации (композитный стержень) представлена на рис. 18. Стержень выполнен из ортогонально армированного линейно-упругого композита, часть слоев которого ориентирована в направлении оси x (продольная ось стержня), а остальная часть – в направлении оси y. Общая толщина стенки h

Рис. 18. Композитный стержень как объект оптимизации

21

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

является суммой толщин продольных слоев h0 и кольцевых слоев h90. Полагается, что продольные и кольцевые слои равномерно перемешаны по толщине стенки, так что материал можно считать однородным. Характеристики однонаправленного композита считаются одинаковыми в продольных и кольцевых слоях.

Для описания свойств многослойной конструкции используется простейшая «нитяная модель», в соответствии с которой жесткость связующего считается пренебрежимо малой в сравнении с жесткостью волокон. Таким образом, из всех констант упругости однонаправленного композита ненулевым является лишь продольный модуль упругости E1, тогда как поперечный модуль упругости, модуль сдвига и коэффициенты Пуассона полагаются равными нулю. Считается также, что прочностное разрушение многослойного материала может быть связано только с разрушением волокон в осевых слоях (кольцевые слои при сделанных допущениях не несут никакой нагрузки и нужны только для обеспечения устойчивости).

Варьируемыми параметрами являются радиус стержня R и

толщины обеих групп слоев h0 и h90:

причем условие тонкостенности (3) должно оставаться в силе при любых изменениях проекта. Для аналитического решения задачи удобнее записать вектор варьируемых параметров в несколько измененном виде:

где символом ˜ обозначена относительная толщина осевых слоев, h0

Диапазоны варьирования значений радиуса и толщины не ограничены; варьирование относительной толщины осевых слоев ограничено естественными границами:

Следует обратить внимание на то, что диапазон варьирования значений относительной толщины не включает граничные точки; таким образом, при любых изменениях проекта в нем должны оставаться обе группы слоев.

22

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Директивными параметрами являются длина L и свойства материала стержня (в соответствии со сделанными допущениями необходимо знать плотность материала ρ, модуль упругости в продольном направлении E1 и предел прочности при продольном сжатии F1−), а также коэффициент устойчивости k [2].

Критериями качества являются масса стержня G и предельно допустимая нагрузка Pпред (отношение Pпред/P составляет запас по несущей способности конструкции). Масса должна быть минимизирована, а предельная нагрузка — максимизирована.

Таким образом, имеет место задача векторной оптимизации (5), (6). Для несущей способности справедливо условие (7). Вместо формулы (8) можно записать

вместо (10) согласно [2] для ортотропной оболочки следует принять

Необходимо иметь в виду, что формула (41) верно описывает лишь осесимметричные формы оболочечной потери устойчивости. Во многих случаях возможны также неосесимметричные формы, которые не описываются формулой (41). Таким образом, для реальных композитных стержней полученные аналитические решения обязательно должны быть проверены при уточненном расчете с учетом всех форм потери устойчивости.

Решение задачи векторной оптимизации проводится в соответствии с рассмотренной в подразд. 1.1 схемой. Формулируется вспомогательная скалярная задача (11), затем эта задача упрощается до вида (12), после чего радиус выражается через массу и толщину по формуле (13). Подставив формулу (13) в формулы (39)—(41), можно получить выражения для составляющих несущей способности

23

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

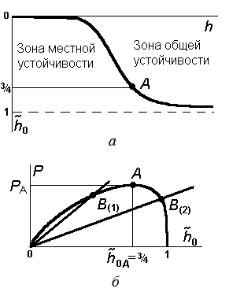
Рис. 19. К решению задачи оптимизации ортогонально армированного композитного стержня

стержня фиксированной массы:

Зависимости (42) изображены на рис. 19 в виде поверхностей в трехмерном пространстве. На рис. 19, а показано условие прочности, зона прочности находится под наклонной плоскостью; под изображенной на рис. 19, б поверхностью находится зона общей устойчивости, а под поверхностью, показанной на рис. 19, в, — зона местной устойчивости.

Теперь следует совместить графики, показанные на рис. 19, и отыскать максимум предельной нагрузки в зоне обеспечения несущей способности, которая находится под всеми тремя поверхностями.

Поскольку сразу представить себе эту зону непросто, сначала нужно построить линию пересечения второй и третьей зависимостей (42) — линию равноустойчивости (рис. 20, а). Проекция этой линии на плоскость варьируемых параметров изображена на рис. 20, а. Уравнение показанной на рис. 20, а линии записывается

24

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

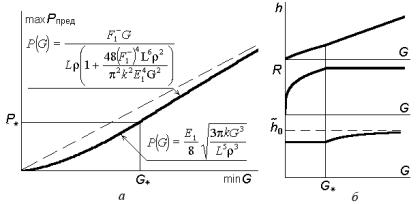
Рис. 20. Линия равноустойчивости (а) и положение на ее проекции оптимальных точек (б)

Слева от линии равноустойчивости (см. рис. 20, а) находится зона местной устойчивости, справа — зона общей устойчивости. В обеих зонах предельная нагрузка возрастает по направлению к линии равноустойчивости. Следовательно, максимум устойчивости конструкции должен находиться где-то на этой линии. Подставив выражение (43) во вторую или третью зависимость (42), можно определить предельную нагрузку равноустойчивости вдоль рассматриваемой линии:

Зависимость (44) имеет один экстремум, положение которого не

25

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

зависит от директивных параметров задачи. Этот экстремум реализуется в точке A, для которой относительная толщина осевых слоев равна 3/4; прочие варьируемые параметры определяются из условий (43) и (13).

На рис. 20, б показаны возможные положения следа плоскости прочности. Если эта плоскость проходит выше точки A, пересекаясь с линией равноустойчивости в точке B(1), то найденная точка A определяет максимум несущей способности. Если же плоскость прочности проходит ниже точки A, то искомый экстремум находится в точке пересечения этой плоскости с линией равноустойчивости, как это показано на рис. 20, б точкой B(2).

Координаты указанных на графиках точек A, B:

Как и в ранее рассмотренных задачах (см. подразд. 1.2), в обоих случаях увеличение предельной нагрузки Pпред невозможно без увеличения массы G. Таким образом, подтверждается допущение (12) и полученные формулы можно считать решением задачи (11).

Решение (45), (46) справедливо при неравенстве ˜ ˜ , ре- h0A > h0B

шение (47), (48) — в обратном случае. Указанное неравенство можно разрешить относительно массы. Критическое значение массы и соответствующее ему значение нагрузки могут быть определены

26

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

формулами

Результат решения задачи оптимального проектирования показан на рис. 21. Граница предельных возможностей построена в координатах требований «минимум массы — максимум несущей способности». Область под кривой (выделенной жирным на рис. 21, а) соответствует достижимым уровням требований к свойствам конструкции. При оптимальном проектировании связь между доступными значениями массы и предельной нагрузки соответствует границе области. Точки, находящиеся вне области, не могут быть достигнуты при проектировании.

Рис. 21. Граница предельных возможностей в задаче оптимального проектирования композитного стержня с ортогонально армированной структурой (а) и оптимальные значения варьируемых параметров (б)

Следует обратить внимание на то, что при G → ∞ предельная нагрузка асимптотически приближается снизу к линейной зависимости (20), в которой [ σ] = F1−; эта зависимость показана на рис. 21 штриховой линией. Оптимальные значения варьируемых параметров приведены на рис. 21, б. Необходимо отметить, что при значениях массы и нагрузки меньше значений, указанных в (49), оптимальная структура армирования постоянна и соответствует соотношению «один кольцевой слой на три осевых слоя»;

27

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

при больших значениях массы и нагрузки доля осевых слоев постепенно увеличивается, асимптотически стремясь к единице. Напротив, оптимальные значения радиуса возрастают при значениях масс и нагрузок, меньше значений, указанных в (49), и остаются постоянными при достижении указанного в (49)значения. Это означает, что при очень больших значениях массы и нагрузки становится несправедливым условие тонкостенности (3), что делает неправомерным применение полученных решений. Однако для большинства практических задач условие (3) остается в силе.

2. МЕТОДИКА ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ

По итогам выполнения домашнего задания должен быть оформлен отчет, который включает в себя номер варианта и исходные данные, а также необходимые формулы, графики и результаты вычислений в соответствии с алгоритмами, приведенными в этом разделе. Результаты всех расчетов следует приводить с точностью до трех значащих цифр.

Примеры оформления домашнего задания приведены в разд. 3. Оформленное домашнее задание представляется на защиту, во время которой студент должен быть готов ответить на вопросы по

материалу, приведенному в разд. 1.

2.1. Задача оптимального проектирования стержня из изотропного материала

при наличии ограничений

Схема объекта проектирования показана на рис. 1. Исходными данными задачи являются:

•длина стержня L;

•минимальная толщина hmin;

•максимальный радиус Rmax;

•свойства изотропного материала — модуль упругости E, предельное напряжение при сжатии [ σ], плотность ρ;

•коэффициент устойчивости k;

•масса конструкции G или расчетная нагрузка P.

28

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

Задача оптимизации является двухмерной; искомые варьируемые параметры — толщина и радиус стержня.

При выполнении домашнего задания рекомендуется такая последовательность действий:

L2 2k

исопоставить ее значение с заданным значением hmin;

2)определить тип оптимизационной задачи, воспользовавшись соотношениями (21), (24), (29) и (32);

3)для заданного типа задачи изобразить границу предельных возможностей аналогично изображенным на рис. 8, 11, 14 или 17. Указать на графиках критические значения массы согласно формулам (22), (25), (26), (30) и (33) и соответствующие им значения нагрузки по (23), (27), (28), (31) или (34) (выбрать нужные формулы для заданного типа задачи);

4)для участка графика, соответствующего заданным значениям G или P, воспользоваться зависимостью, связывающей эти характеристики (указаны на графиках рис. 8, 11, 14 или 17), для определения нагрузки, если задана масса, и для определения массы, если задана нагрузка;

29

Copyright ОАО «ЦКБ «БИБКОМ» & ООО «Aгентство Kнига-Cервис»

5)определить оптимальные параметры проектируемого стержня по зависимостям, приведенным в подраз. 1.2. Указать, является ли полученное решение единственным (единственность решения может быть исследована с помощью графиков, приведенных на рис. 7, 10, 13 и 16; в случае множества решений следует указать границы диапазонов оптимальных значений толщины и радиуса);

6)рассчитать предельные значения нагрузок по прочности — по формуле (8), по общей устойчивости — по формуле (9), местной устойчивости — по формуле (10). Сделать вывод о несущей способности спроектированной конструкции.

2.2. Задача оптимального проектирования композитного стержня

с ортогонально армированной структурой

Схема объекта проектирования показана на рис. 18. Исходными данными задачи являются:

•длина стержня L;

•свойства однонаправленного композиционного материала (композита):

•модуль упругости вдоль волокон E1,

•предельное напряжение при сжатии вдоль волокон F1−,

•плотность ρ;

•коэффициент устойчивости k;

•масса конструкции G или расчетная нагрузка P.

Задача оптимизации является трехмерной. Искомые варьируемые параметры: толщина и радиус стержня, а также относительная доля продольных слоев в структуре композита.

При выполнении домашнего задания рекомендуется такая последовательность действий:

1)рассчитать критическое значение массы и соответствующее значение нагрузки по формулам (49);

2)изобразить границу предельных возможностей аналогично рис. 21. Указать на графике критическое значение массы и соответствующее значение нагрузки, а также точку, соответствующую заданной массе G или заданной нагрузке P;

3)для участка графика, соответствующего заданным значениям G или P, воспользоваться зависимостью (46) или (48) для опреде-

30