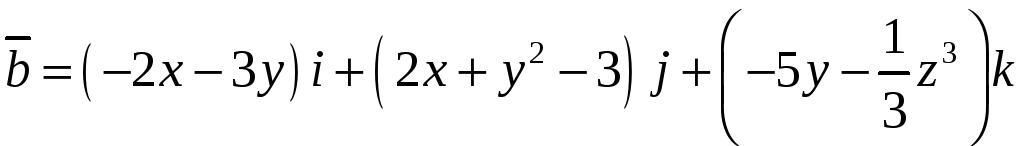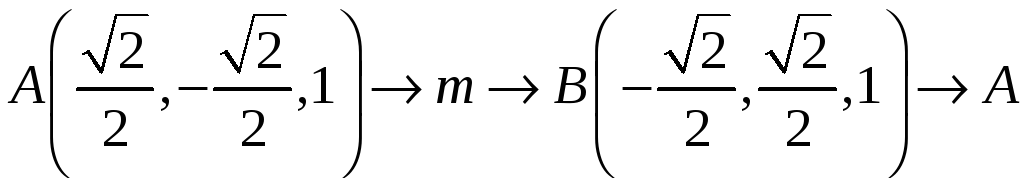ДЗ Криволинейные и поверхн.Теор.поля 2 к.3 с
.doc
Табл.11.
|
Вар. |
Векторное
поле
|
Плоскость |
Ось |
|
1 |
|
|
OX |
|
2 |
|
|
OY |
|
3 |
|
|
OZ |
|
4 |
|
|
OX |
|
5 |
|
|
OY |
|
6 |
|
|
OZ |
|
7 |
|
|
OX |
|
8 |
|
|
OY |
|
9 |
|
|
OZ |
|
10 |
|
|
OY |
|
11 |
|
|
OZ |
|
12 |
|
|
OZ |
|
13 |
|
|
OY |
|
14 |
|
|
OZ |
|
15 |
|
|
OZ |
|
16 |
|
|
OX |
|
17 |
|
|
OZ |
|
18 |
|
|
OY |
|
19 |
|
|
OZ |
|
20 |
|
|
OX |
|
21 |
|
|
OX |
|
22 |
|
|
OY |
|
23 |
|
|
OZ |
|
24 |
|
|
OX |
|
25 |
|
|
OZ |
|
26 |
|
|
OZ |
|
27 |
|
|
OX |
|
28 |
|
|
OX |
|
29 |
|
|
OZ |
|
30 |
|
|
OY |
Задача
5.
Дано векторное поле
-
Проверить, что это поле является потенциальным.
-
Найти потенциал поля
-
Найти уравнение линий равного потенциала и изобразить линии равного потенциала на чертеже.
-
Составить уравнение векторных линий поля
и изобразить векторные линии на том
же чертеже, указав стрелками направление
векторных линий. -
Вычислить линейный интеграл
.
|
Вар. |
Векторное поле |
Точка A |
Точка B |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
|
7 |
|
|
|
|
8 |
|
|
|
|
9 |
|
|
|
|
10 |
|
|
|
|
11 |
|
|
|
|
12 |
|
|
|
|
13 |
|
|
|
|
14 |
|
|
|
|
15 |
|
|
|
|
16 |
|
|
|
|
17 |
|
|
|
|
18 |
|
|
|
|
19 |
|
|
|
|
20 |
|
|
|
|
21 |
|
|
|
|
22 |
|
|
|
|
23 |
|
|
|
|
24 |
|
|
|
|
25 |
|
|
|
|
26 |
|
|
|
|
27 |
|
|
|
|
28 |
|
|
|
|
29 |
|
|
|
|
30 |
|
|
|
Задача
6. Дано
векторное поле
.
-
Найти дивергенцию векторного поля
,
исследовать расположение источников
и стоков векторных линий поля. -
Найти поток векторного поля
через замкнутую поверхность
. -
Найти ротор векторного поля
. -
Вычислить циркуляцию поля
вдоль замкнутой линии
двумя способами: а) преобразовав
линейный интеграл в определенный с
использованием уравнений линии
;
б) преобразовав линейный интеграл в
поверхностный с помощью теоремы Стокса.
-
Выяснить, как изменится циркуляция поля
вдоль контура
,
если изменить расположение контура в
данном поле. Найти наибольшее значение
циркуляции для данного контура.
|
Вар. |
Поле
|
|
1 |
|
|
2 |
двух
отрезков прямых
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
|
7 |
|
|
8 |
|
|
9 |
|
|
10 |
|
|
11 |
|
|
12 |
|
|
13 |
диаметра
|
|
14 |
|
|
15 |
|
|
16 |
|
|
17 |
|
|
18 |
диаметра
|
|
19 |
|
|
20 |
|
|
21 |
|
|
22 |
|
|
23 |
диаметра
|
|
24 |
|
|
25 |
диаметра
|
|
26 |
|
|
27 |
|
|
28 |
двух
отрезков прямых
|
|
29 |
|
|
30 |
|
:
- поверхность, ограничивающая тело Т
-
замкнутая
линия
-контур
прямоугольника с вершинами
состоит
из дуги окружности
и
и
,
-контур
треугольника с вершинами
-контур
треугольника с вершинами
-контур
параллелограмма с вершинами
-контур
параллелограмма с вершинами
-контур
треугольника с вершинами
-контур
параллелограмма с вершинами
-контур
треугольника с вершинами
-контур
треугольника с вершинами
-контур
треугольника с вершинами
-контур
треугольника с вершинами
состоит
из дуги эллипса
и его
:
-эллипс
обходимый в направлении
-контур
треугольника с вершинами
-контур
прямоугольника с вершинами
-контур
треугольника с вершинами
состоит
из дуги окружности
и ее
:
-контур
параллелограмма с вершинами
-контур
треугольника с вершинами
-контур
ромба с вершинами
-контур
прямоугольника с вершинами
состоит
из дуги эллипса
:
и его
,
-контур
треугольника с вершинами
состоит
из дуги окружности
и ее
:
-
контур ромба с вершинами
-контур
треугольника с вершинами
-
состоит из дуги окружности
и
и
:
-контур
параллелограмма с вершинами
-контур
прямоугольника с вершинами
