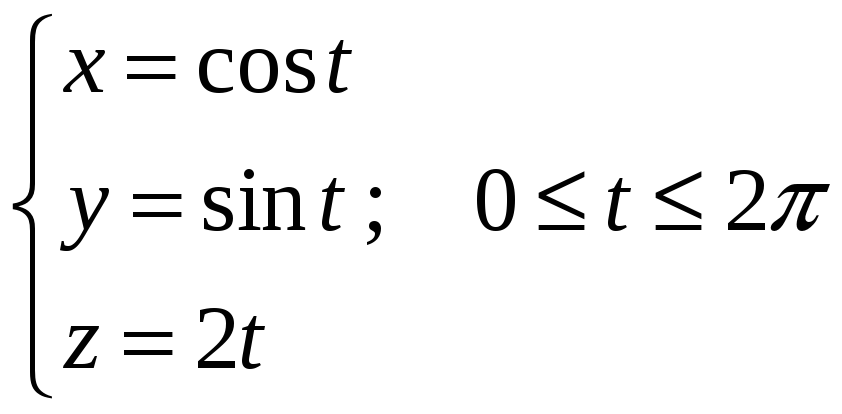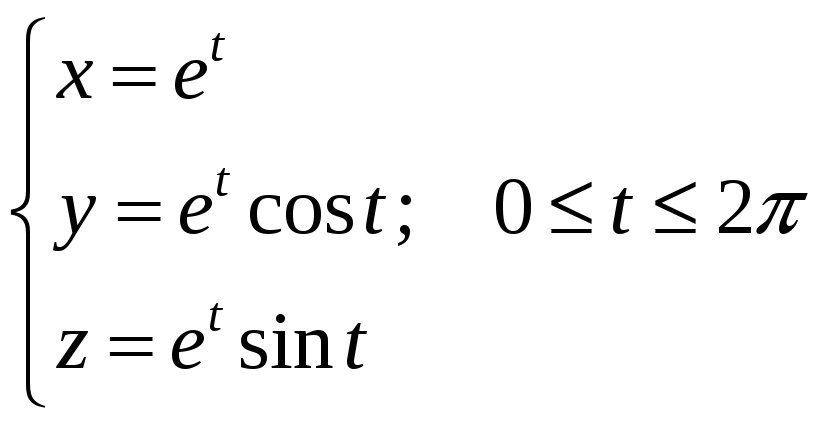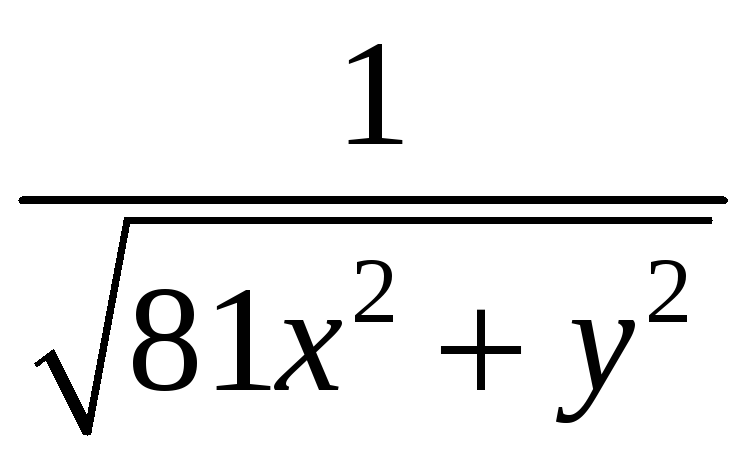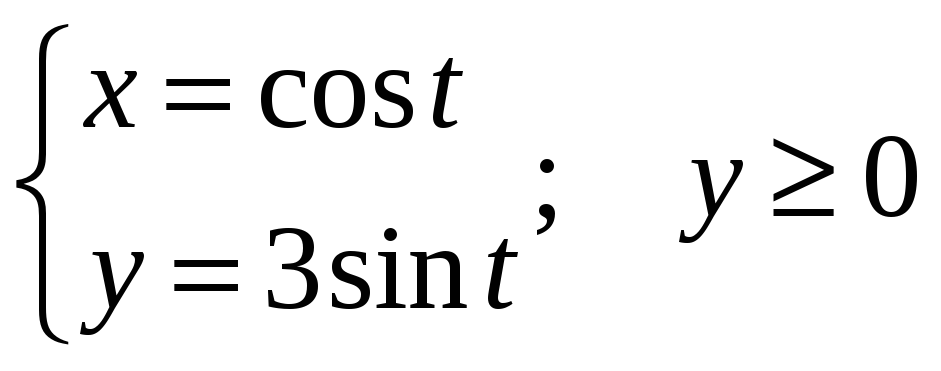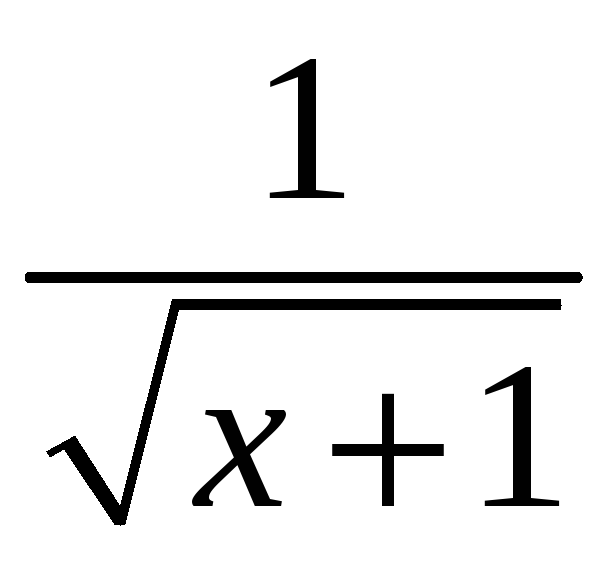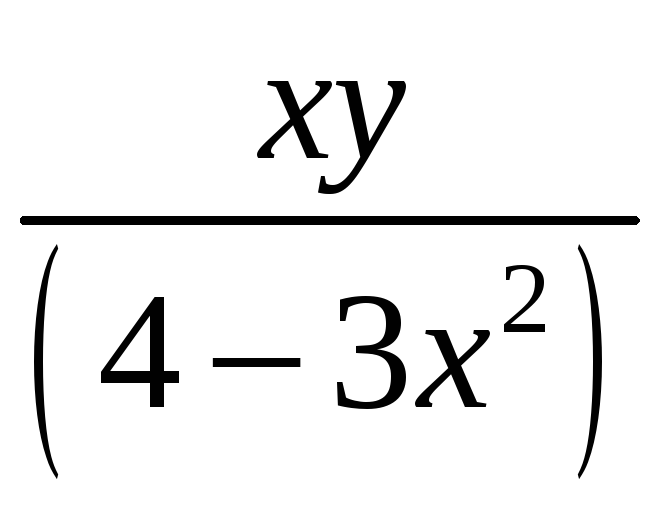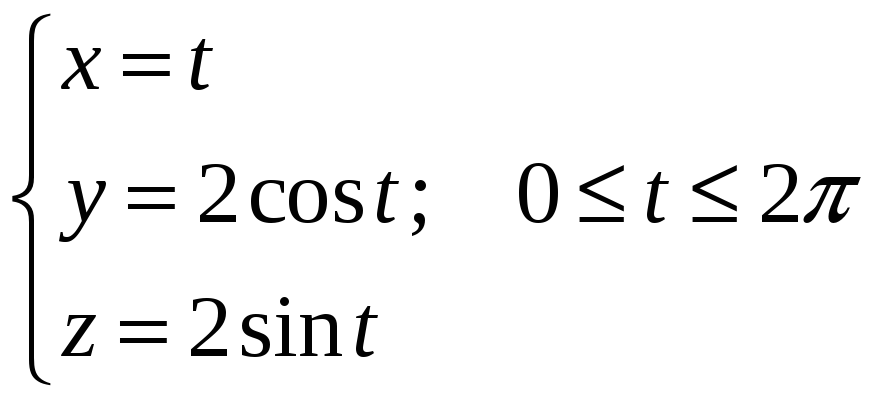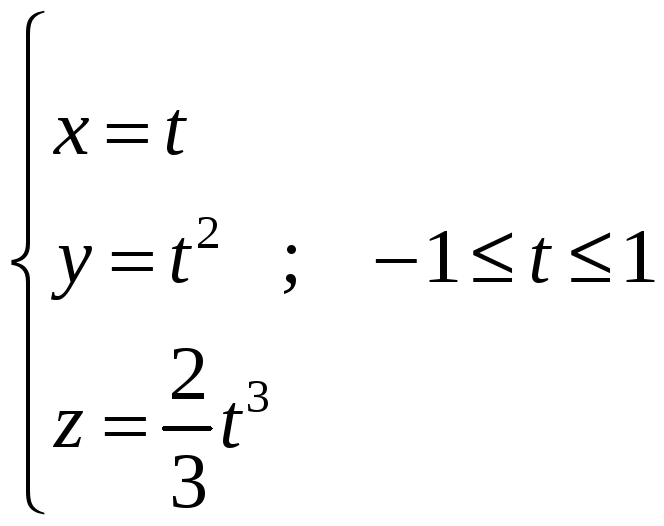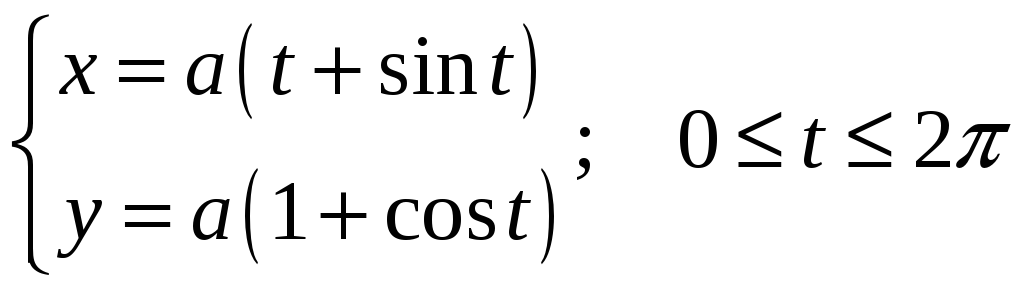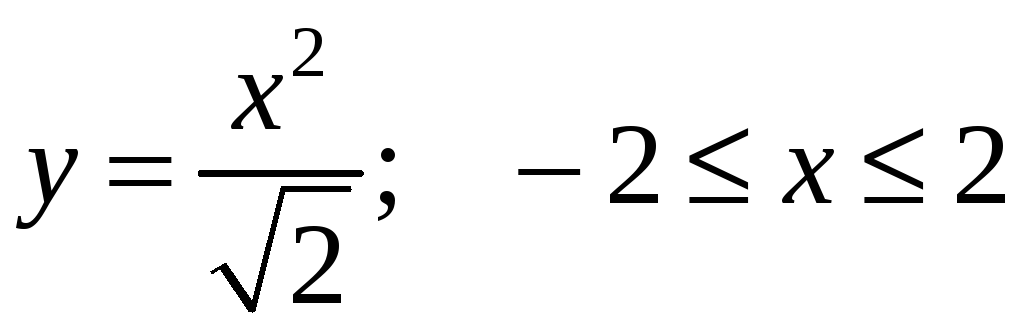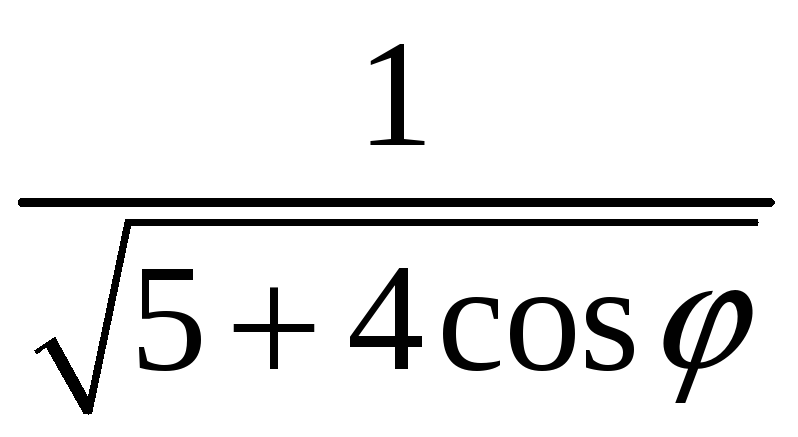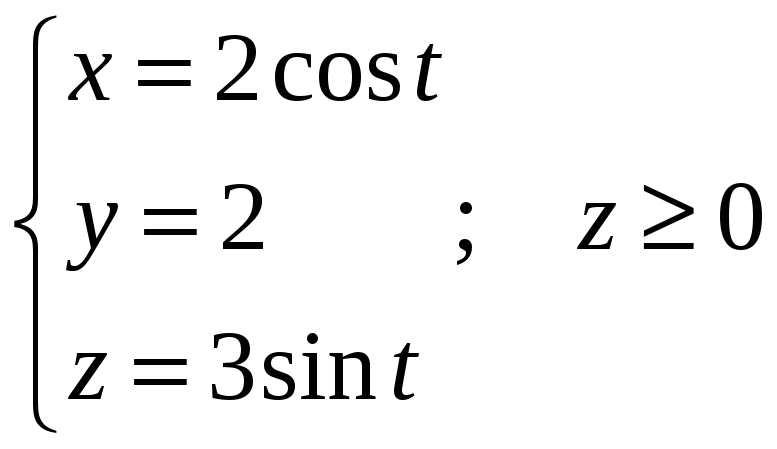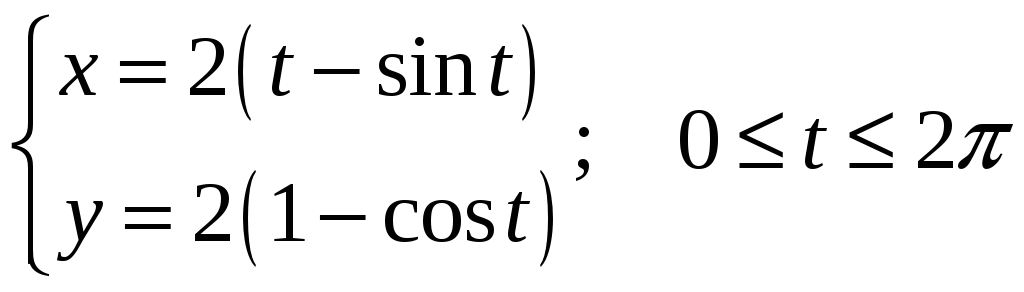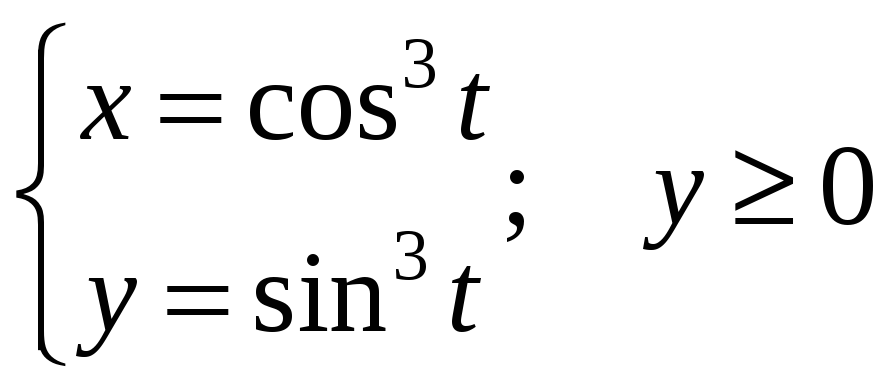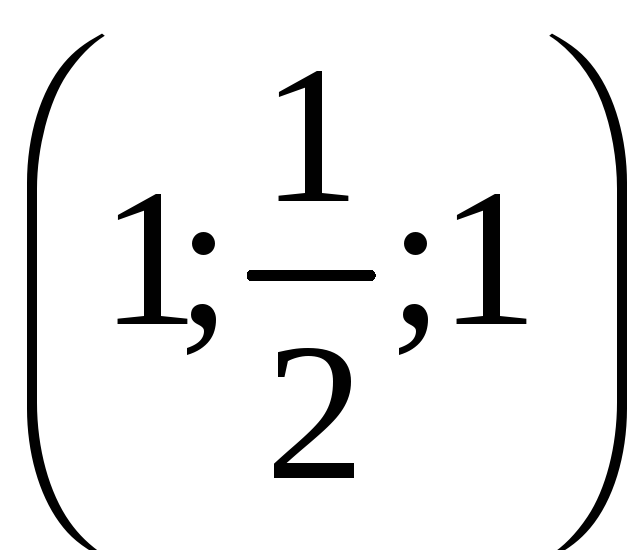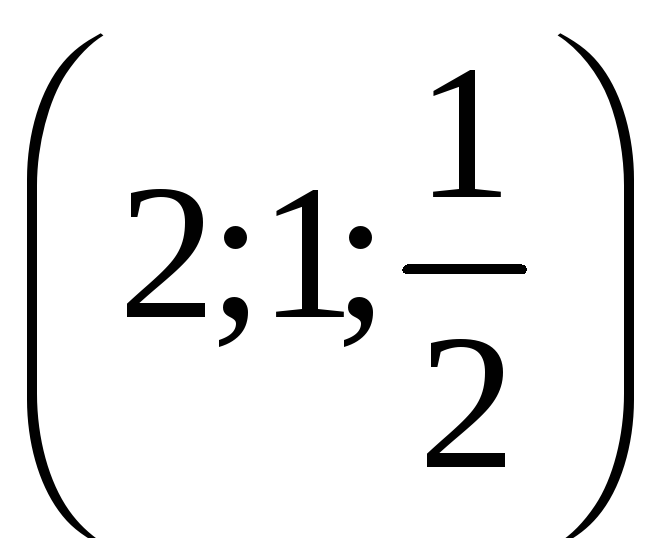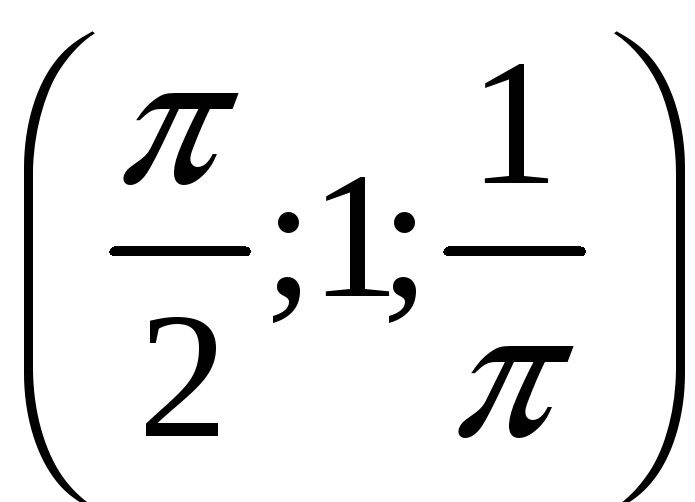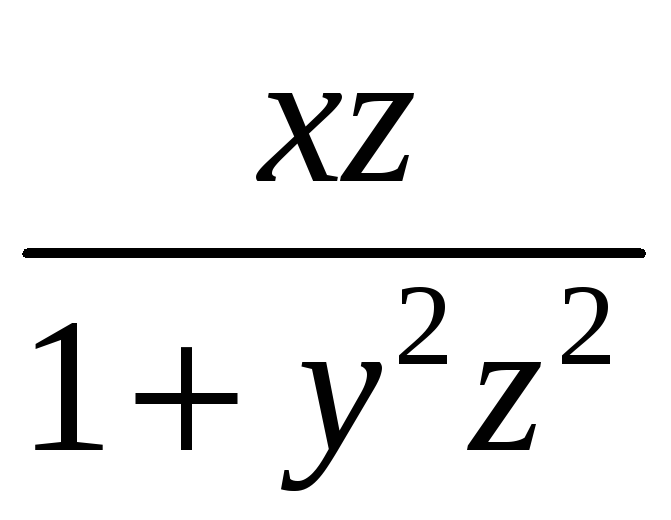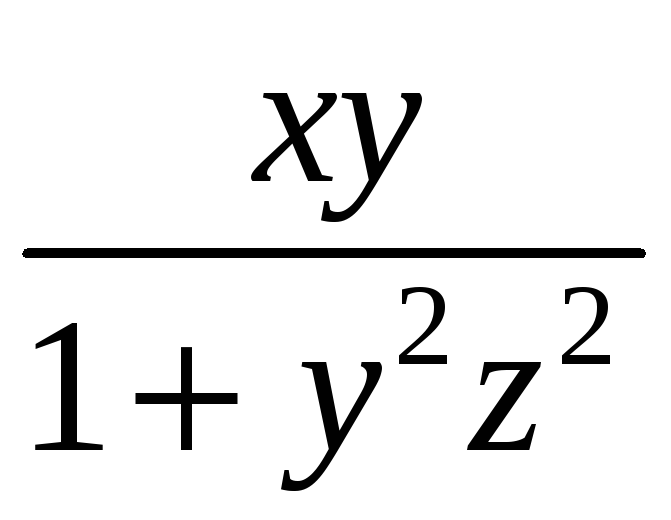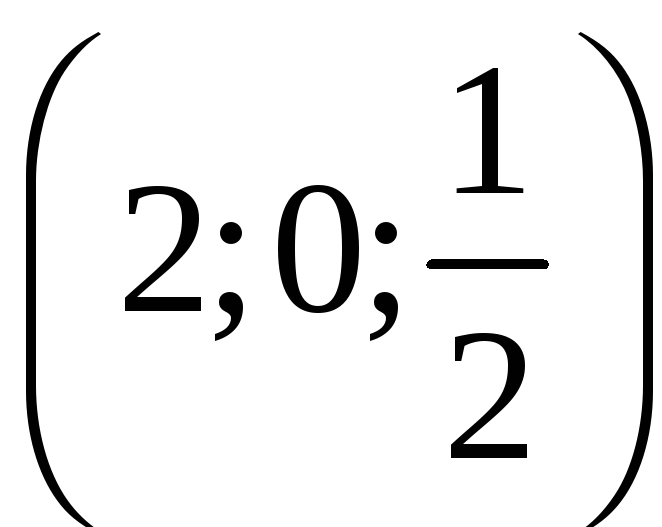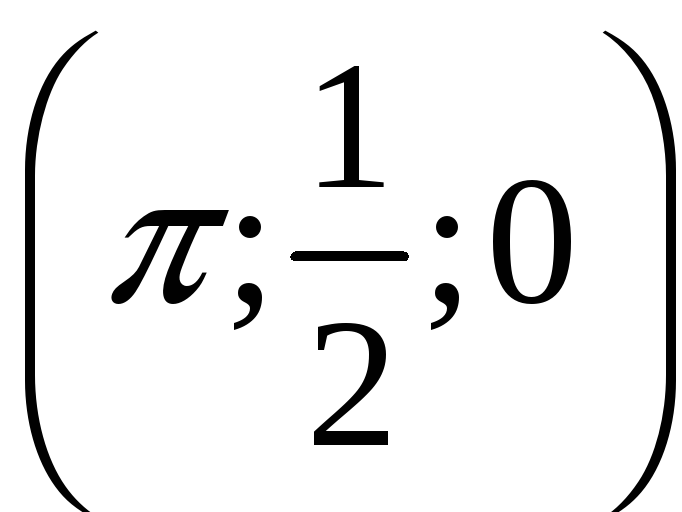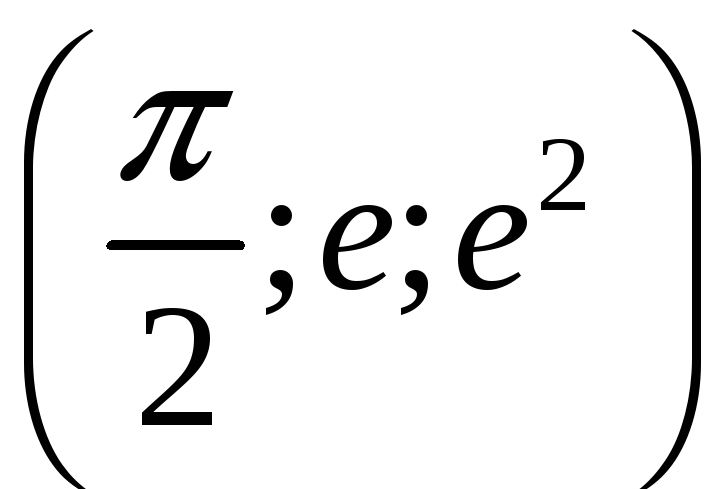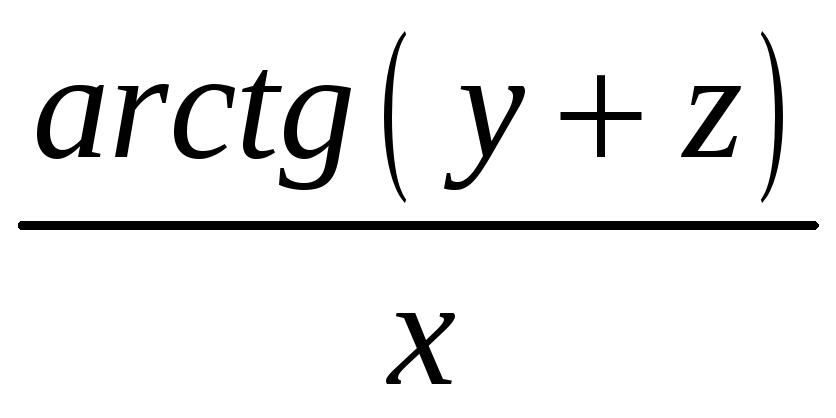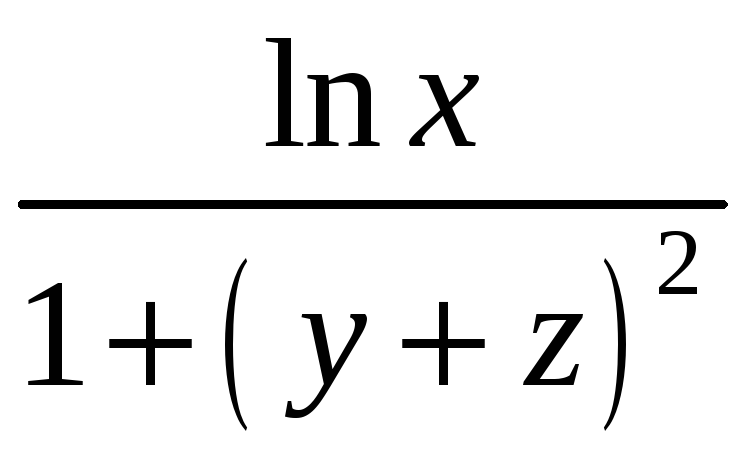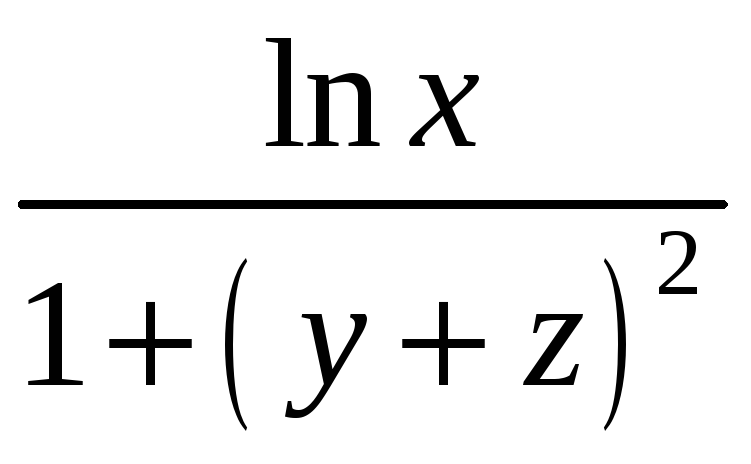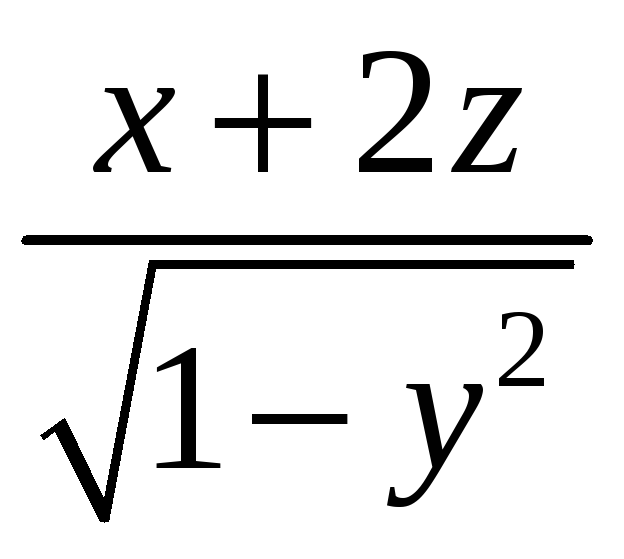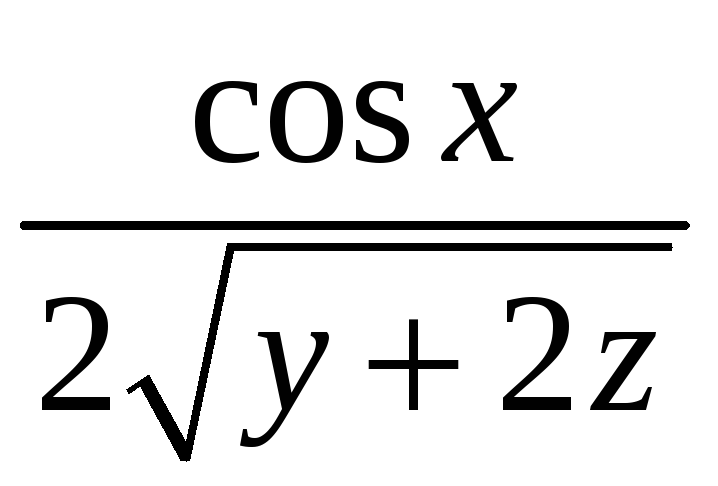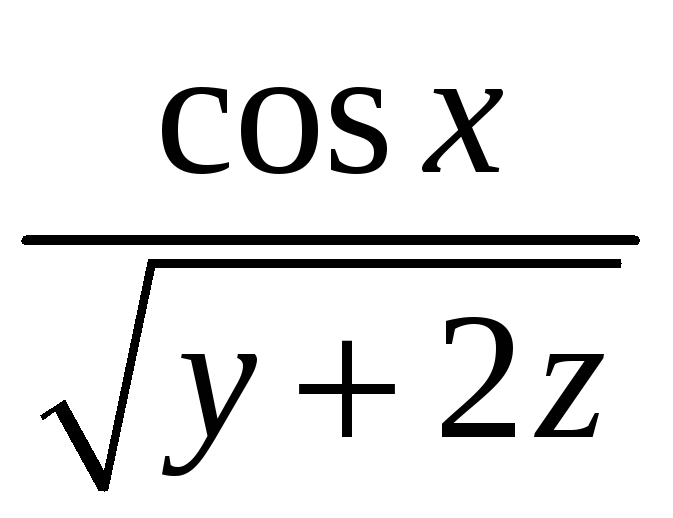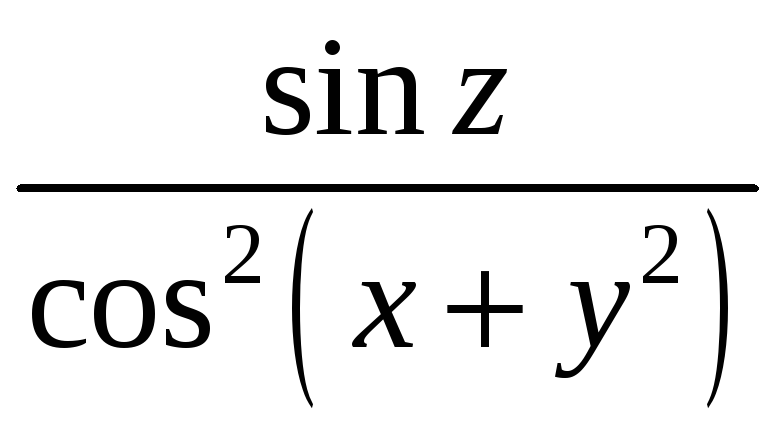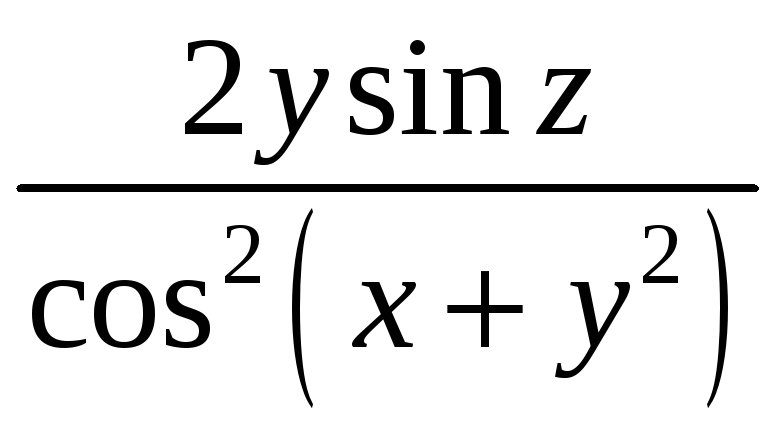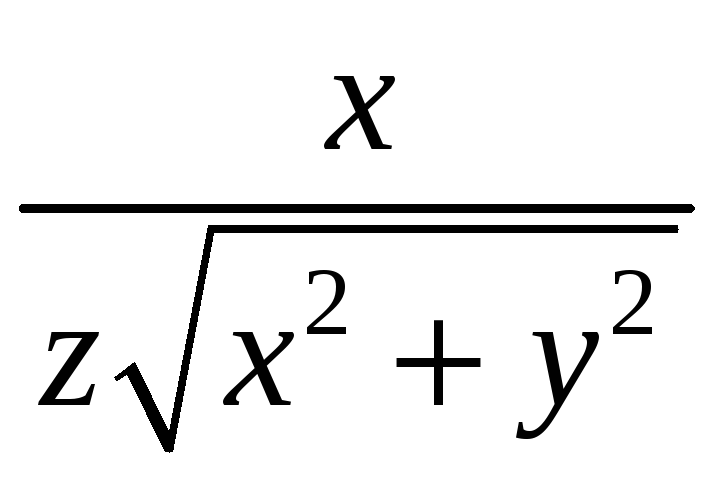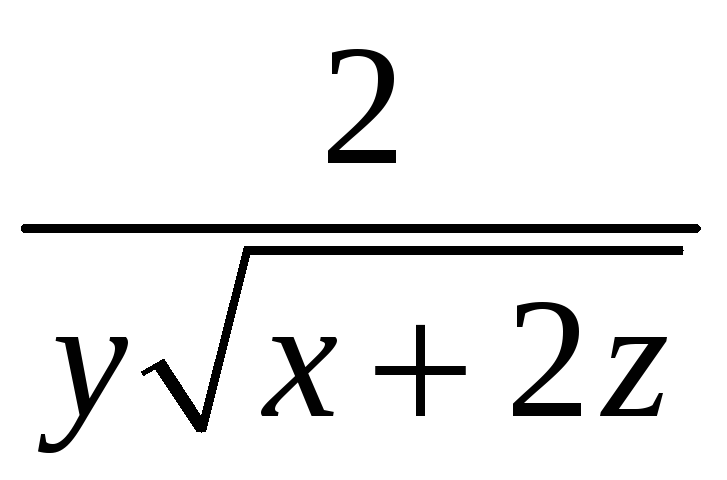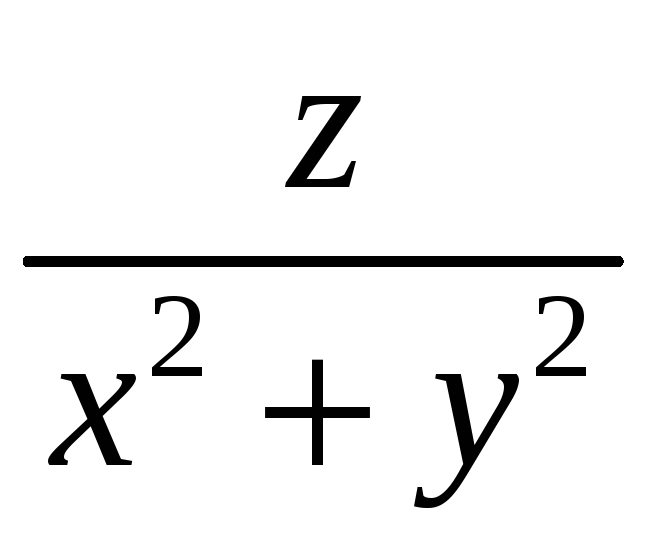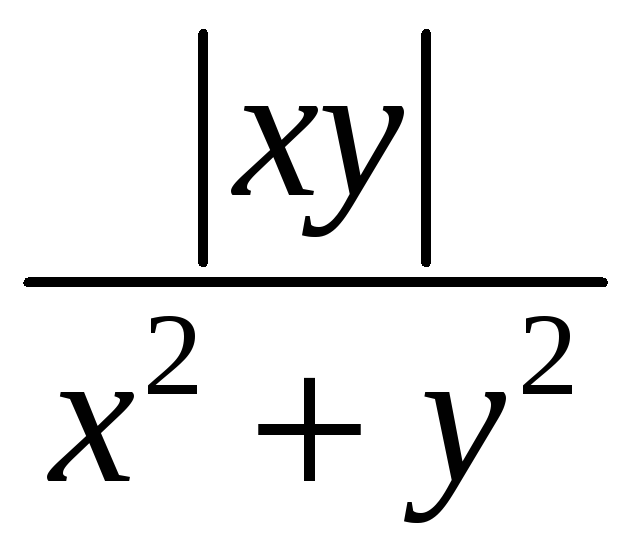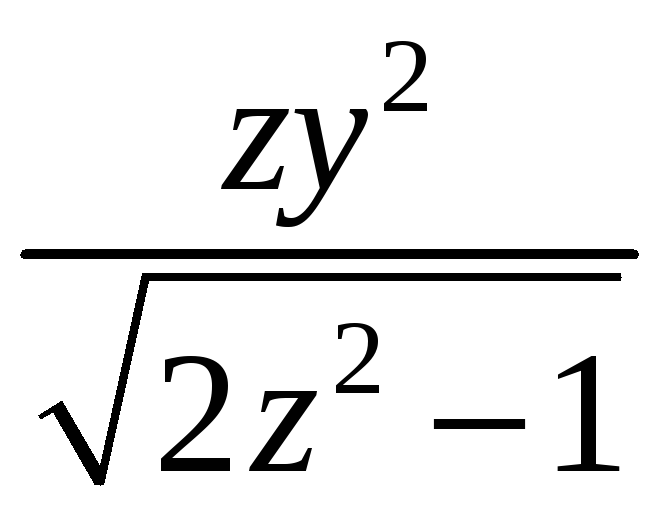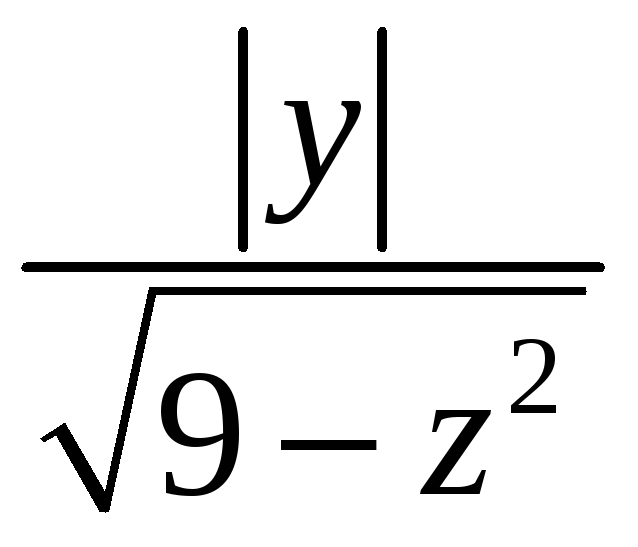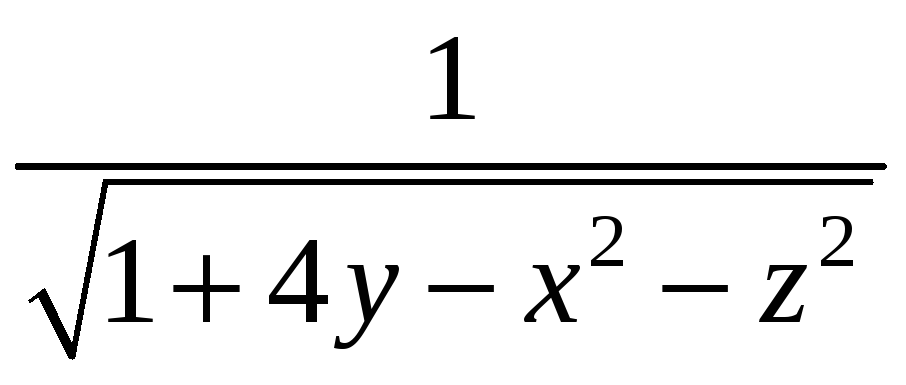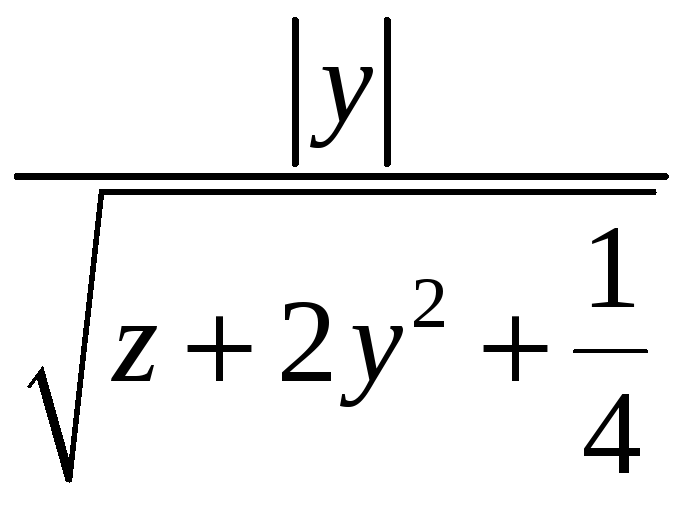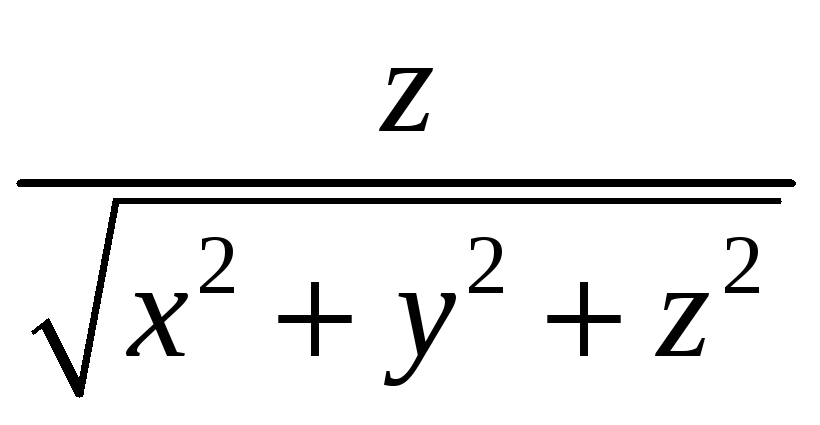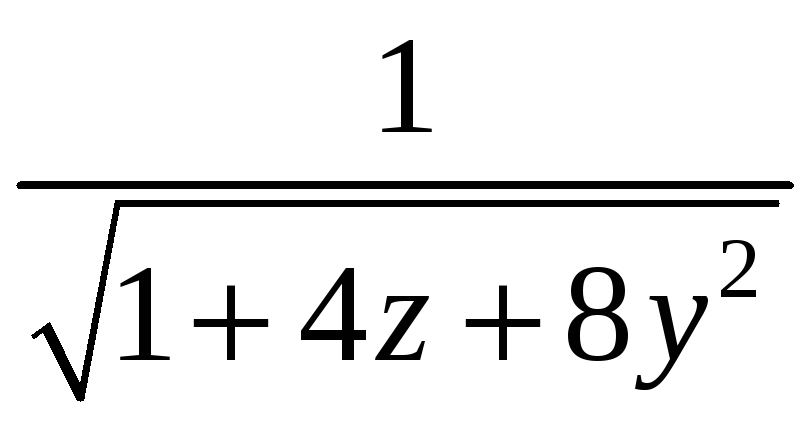ДЗ Криволинейные и поверхн.Теор.поля 2 к.3 с

ДЗ № 2. КРИВОЛИНЕЙНЫЕ И ПОВЕРХНОСТНЫЕ ИНТЕГРАЛЫ. ТЕОРИЯ ПОЛЯ.

ЗАДАЧА 1. В вариантах 1-10: найти момент инерции кривой относительно начала координат. В вариантах 11-20: найти массу кривой С. В вариантах 21-30: найти центр масс кривой С. Плотность кривой С и уравнение кривой С даны в табл.8.

ЗАДАЧА 2. В вариантах 1-15 вычислить криволинейный интеграл , убедившись в том, что подинтегральная функция является полным дифференциалом. Координаты точек А и В, а также функции Р(x,y,z) , Q(x,y,z), R(x,y,z) даны в табл.9. В вариантах 16-30: найти функцию V(x,y,z) по ее полному дифференциалу (dV=Pdx+Qdy+Rdz) c помощью вычисления криволинейного интеграла. Функции P(x,y,z), Q(x,y,z), R(x,y,z) даны в табл. 9.

ЗАДАЧА 3. Дана поверхность плотности . В вариантах 1-10 найти массу поверхности. В вариантах 11-20 найти координаты центра тяжести. В вариантах 21-30 найти моменты инерции относительно осей координат и начала координат. Данные в табл.10.

ЗАДАЧА 4. Найти поток векторного поля F через часть плоскости G, ограниченную координатными плоскостями и расположенную в соответствующем октанте. Сторона плоскости определяется нормалью, образующей острый угол с указанной в таблице осью координат. Данные в табл. 11.

Табл.8.

№ вар.	Плотность	Уравнение кривой
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Табл.9 вар.1-15.

Вар.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

Табл.9 вар.16-30.

Вар.
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30

Табл.10.

Вар.	Поверхность	Плотность
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30