
Уравнения Максвелла и преобразования Лоренца учебно-методическое пособие
..pdf
Тогда функция вида (31) допускает такую интерпретацию. Пусть фиксированному начальному моменту времени t = t0 отвечает неко- торая поверхность уровня
ϕ0(х, y, z) = ωt0.
С течением времени эта поверхность как бы перемещается в про- странстве, занимая последовательно положения с различными, уве- личивающимися значениями ϕi (x, y, z) = ω ti. Такую бегущую по- верхность уровня принято называть волновым фронтом. Если в на- чальный момент времени t = t0 на поверхности волнового фронта за- фиксировать некоторую точку с координатами x0, y0, z0, то при дви- жении фронта волны эта точка опишет некоторую кривую, называе- мую лучом. Радиус-вектор
r(t) = xi + yj + zk
текущей точки на луче является функцией времени, и нашей бли- жайшей целью будет составить дифференциальные уравнения для определения этой функции. Очевидно, что скорость точки на луче
v(t) = dr = dx i + dy j + dz k dt dt dt dt
должна во все время движения оставаться коллинеарной вектору градиента функции ϕ (х, y, z), вычисленного в данной точке. Это по- ложение можно воспринимать и как определение луча.
Положим g = grad ϕ.
Тогда
dr = λg, dt
или в координатной форме
|
dx |
= λ |
∂ϕ , |
||
|
|
|
|
||
|
dt |
∂x |
|||
dy |
= λ |
∂ϕ , |
|||
|
|
||||
|
dt |
∂y |
|||
|
|
|
|
|
(34) |
dz |
= λ |
∂ϕ . |
|||
|
|||||
dt |
∂z |
||||
Коэффициент пропорциональности λ (х, y, z) находится следую- щим образом. Из данных выше определений волнового фронта и лу- ча вытекает тождество
21
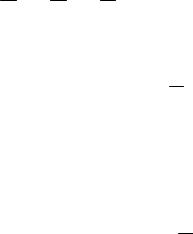
ϕ ( x(t), y(t), z(t)) = ωt,
дифференцируя обе части которого по времени, получим
∂ϕ dx + ∂ϕ dy + ∂ϕ dz = ω
.
∂x dt ∂y dt ∂z dt
Вносим сюда вместо компонент скорости их выражения из урав- нений луча (34). И, с учетом уравнения эйканала (32), найдем
λ = c2 .
ω
Теперь нетрудно вычислить квадрат элемента длины луча ds2 = dr2 = dx2 + dy2 + dz2 .
Принимая во внимание (32), (34) и (35), имеем ds2 = c2 dt2 .
Соответственно, получим величину лучевой скорости
v = c = ds . dt
(35)
(36)
Вводя в систему уравнения луча (34) в качестве переменной дли- ну дуги s, можно представить ее и в такой форме:
dx |
= |
|
|
c |
|
∂ϕ , |
|
|||
ds |
|
|
|
|
||||||
|
|
|
|
ω ∂x |
|
|||||
dy |
|
= |
c |
∂ϕ , |
(37) |
|||||
|
|
|
|
|||||||
ds |
|
|
|
|
ω ∂y |
|
||||
dz |
= |
c |
∂ϕ . |
|
||||||
|
|
|
||||||||
ds |
|
|
|
|
ω ∂z |
|
||||
Системы уравнений луча (34) или (37) содержат в себе, вообще говоря, некую неопределенность в виде неизвестных функций
∂ϕ , |
∂ϕ , |
∂ϕ , так как относительно функции ϕ (x, y, z) известно лишь |
∂x |
∂y |
∂z |
то, что она должна быть одним из решений уравнения эйканала (32). Но по значению только модуля градиента скалярное поле однозначно не восстанавливается. Однако систему уравнений луча возможно преобразовать и во вполне определенную систему, включающую только заданные функции.
22
Запишем следующие тождества:
|
∂g2 |
|
= 2 |
∂ϕ ∂2ϕ + 2 ∂ϕ |
|
|
∂2ϕ |
+ 2 |
∂ϕ |
∂2ϕ |
, |
|||||||||||||||||||||||||||||||||||||
|
∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
∂x ∂x2 |
|
|
∂y ∂x∂y |
|
|
∂z ∂x∂z |
|
|
||||||||||||||||||||||||||||||||||||||
|
∂g2 |
|
= 2 |
∂ϕ |
|
|
∂2ϕ |
+ 2 |
∂ϕ ∂2ϕ + 2 |
∂ϕ |
∂2ϕ |
, |
||||||||||||||||||||||||||||||||||||
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
∂x ∂x∂y |
|
|
|
∂y ∂y2 |
|
|
∂z ∂y∂z |
|
|
|||||||||||||||||||||||||||||||||||||
|
∂g2 |
|
= 2 |
∂ϕ |
|
|
∂2ϕ |
+ 2 |
∂ϕ |
|
|
∂2ϕ |
|
+ 2 ∂ϕ ∂2ϕ |
, |
|||||||||||||||||||||||||||||||||
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
∂x ∂x∂z |
|
|
|
∂y ∂y∂z |
|
|
∂z ∂z2 |
|
|
|||||||||||||||||||||||||||||||||||||
а также |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
d |
∂ϕ = |
∂2ϕ |
dx |
+ |
|
∂2ϕ |
|
dy |
+ |
|
∂2ϕ |
|
|
|
|
dz |
, |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
dt ∂x |
∂x2 dt |
∂x∂y dt |
|
∂x∂z dt |
|
|
|||||||||||||||||||||||||||||||||||||||||
|
d |
∂ϕ = |
∂2ϕ |
|
|
dx |
+ |
|
∂2ϕ |
dy |
+ |
|
∂2ϕ |
|
|
dz |
, |
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
dt ∂y |
∂x∂y dt |
|
|
∂y2 dt |
|
∂y∂z dt |
|
|
|||||||||||||||||||||||||||||||||||||||
|
d |
∂ϕ = |
∂2ϕ |
|
dx |
+ |
|
∂2ϕ |
|
dy |
+ ∂2ϕ |
dz |
. |
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
dt ∂z |
∂x∂z dt |
|
|
∂y∂z dt |
|
∂z2 dt |
|
|
|||||||||||||||||||||||||||||||||||||||
Отсюда, с учетом уравнений луча (34), |
||||||||||||||||||||||||||||||||||||||||||||||||
|
d |
∂ϕ = |
c2 |
|
∂ |
|
g2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt ∂x |
2ω ∂x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
d |
∂ϕ = |
c2 |
|
∂ |
g2 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt ∂y |
2ω ∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
d |
∂ϕ = |
c2 |
|
∂ |
g2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
dt ∂z |
2ω ∂z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
или, заменяя здесь квадрат градиента его значением из уравнения эйканала (32),
d |
∂ϕ = −ω |
∂ |
|
ln c, |
|
|
|
|
|
|
|||
dt ∂x |
∂x |
|
||||
d |
∂ϕ = −ω |
∂ |
ln c, |
(38) |
||
|
|
|
||||
dt ∂y |
∂y |
|
||||
d |
∂ϕ = −ω |
∂ |
ln c. |
|
||
|
|
|
||||
dt ∂z |
∂z |
|
||||
Таким образом, вводя в рассмотрение три новые неизвестные функции времени
23
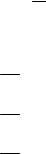
l = |
∂ϕ , m = |
∂ϕ , n = |
∂ϕ |
|
∂x |
∂y |
∂z |
и прибавляя к системе из трех уравнений (34) еще три равенства (38), получим для определения хода луча систему из шести уравнений первого порядка, у которых правые части составлены из заданных функций. А именно
|
|
|
dx |
|
= |
|
c2 |
|
l, |
|
||||||||
|
|
|
dt |
ω |
|
|
|
|
|
|
||||||||
|
|
|
dy |
|
= |
c2 |
|
m, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
dt |
ω |
|
|
|
|
|
|||||||||
|
|
|
dz |
= |
c2 |
|
n, |
|
||||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
dt |
ω |
|
|
|
|
|
|||||||||
dl |
|
= −ω |
|
∂ |
ln c, |
|
||||||||||||
|
|
|
|
|||||||||||||||
dt |
∂x |
|
|
|
|
|
||||||||||||
dm |
= −ω |
∂ |
ln c, |
(39) |
||||||||||||||
|
|
|
|
|||||||||||||||
dt |
|
|
∂y |
|
||||||||||||||
dn |
= −ω |
|
∂ |
ln c. |
|
|||||||||||||
|
|
|
|
|||||||||||||||
dt |
|
∂z |
|
|||||||||||||||
В качестве текущей лучевой координаты может быть выбран лю- бой удобный параметр. Система (39) приобретет еще более компакт- ную форму, если вместо времени t ввести лучевой параметр σ, опре- делив его дифференциал так:
dσ = c2 dt.
ω
При этом переменная σ имеет размерность площади ([σ] = м2). Теперь система (39) принимает вид
dx = l, dσ
dy = m, dσ
dz = n, dσ
24

dl |
|
= ω2 |
|
∂ |
|
|
|
1 |
|
, |
|||
dσ |
|
|
|
|
|
|
|||||||
|
2 ∂x c2 |
|
|
||||||||||
dm |
= ω2 |
∂ |
|
|
1 |
|
|
, |
|||||
|
|
|
|
|
|
||||||||
dσ |
|
2 ∂y c2 |
|
|
|||||||||
dn |
|
= ω2 |
∂ |
|
1 |
. |
|||||||
dσ |
|
|
|
||||||||||
|
2 ∂z c2 |
|
|
||||||||||
Из этой системы, конечно, можно исключить три неизвестные функции l, m, n и получить систему из трех уравнений второго по- рядка:
d 2 x = ω2 dσ2 2
d 2 y = ω2 dσ2 2
d 2 z = ω2 dσ2 2
∂1
∂x c2 ,
∂1
∂y c2 ,
∂1
∂z c2 .
Если возвратиться к первоначальному аргументу t, означающему время, то получится такая система трех уравнений второго порядка:
d |
2 |
x |
|
= −c |
∂c + |
2 |
|
|
|
dx |
|
|
∂c |
dx |
+ |
∂c |
dy |
+ |
∂c dz |
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
dt2 |
∂x c dt |
∂x dt |
∂y dt |
∂z dt |
|||||||||||||||||||||||||||||||||
d |
2 |
y |
= −c |
∂c + |
2 |
|
|
|
dy |
|
|
∂c |
dx |
+ |
∂c |
dy |
+ |
∂c dz |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
dt2 |
∂y c dt |
∂x dt |
∂y dt |
∂z dt |
|||||||||||||||||||||||||||||||||
d |
2 |
z |
= −c |
∂c + |
2 |
|
|
|
dz |
|
|
∂c |
dx |
+ |
∂c |
dy |
+ |
∂c dz |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
, |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
dt2 |
∂z c dt |
∂x dt |
∂y dt |
∂z dt |
|||||||||||||||||||||||||||||||||
которую, очень удобно представить, в векторной форме:
d 2 r |
= −c gradc + |
2 dr |
dr |
|
|||||
|
|
|
|
gradc |
|
|
. |
(40) |
|
dt2 |
c |
dt |
dt |
||||||
25
6.БЛУЖДАЮЩАЯ ВОЛНА
ВНЕОДНОРОДНОЙ СРЕДЕ
Рассмотрим одномерное волновое уравнение
∂2W − |
1 ∂2W |
= 0. |
(41) |
||
|
|
||||
c2 (x) ∂t2 |
|||||
∂x2 |
|
|
|||
Покажем, как найти его частное решение при произвольной функции с(х). Положим
W = X (x) + T (t),
тогда
d 2 X |
− |
1 |
|
d 2T |
= 0. |
dx2 |
c2 (x) |
|
dt2 |
||
|
|
|
Это необходимо приводит к соотношению
c2 (x) |
d 2 X |
= |
|
d 2T |
= λ = const, |
|
|
|
||||
dx2 |
|
dt2 |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
из которого находим выражения для функций X(x) и T(t): |
|
|||||||||||
|
|
|
|
1 |
|
|
T = λ t2 . |
|
|
|||
X (x) = λ∫ ∫ |
|
|
dx dx, |
|
|
|||||||
2 |
|
|
|
|||||||||
|
|
|
|
с (x) |
|
|
2 |
|
|
|
||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
λ t2 . |
|
|
|
|
|
|
W = λ∫ |
∫ |
|
dx dx + |
(42) |
|||
|
|
|
|
|
|
2 |
||||||
|
|
|
|
|
|
|
|
с |
(x) |
|
2 |
|
В полученном решении можно выделить слагаемые, соответст- вующие волнам, бегущим в противоположных направлениях. Преоб-
|
∫ |
|
∫ |
1 |
|
|
разуем интеграл |
|
dx dx. |
||||
с2 (x) |
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
||
∫ |
|
∫ |
|
|
|
dx dx = ∫ |
∫ |
|
d ∫ |
|
|
dx dx = |
|
|||||||||||
|
|
2 |
|
|
|
с(x) |
|
|||||||||||||||||
|
|
|
|
с |
(x) |
|
|
|
|
с(x) |
|
|
|
|
|
|||||||||
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
||||||
|
|
|
|
|
|
|
|
c′(x) |
|
|||||||||||||||
= |
|
|
|
|
|
|
|
|
dx dx + |
|
|
|
|
|
|
|
dx dx dx. |
|||||||
∫ |
с(x) ∫ с(x) |
∫ |
с2 |
(x) |
∫ с(x) |
|||||||||||||||||||
|
|
|
|
|
∫ |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Заметим, что
26
|
|
1 |
|
|
|
|
1 |
|
|
|
1 |
|
1 |
|
||||||
∫ |
|
|
|
|
|
|
|
dx dx = |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
c(x) ∫ с(x) |
|
|
2 ∫ с(x) |
|||||||||||||||||
Поэтому |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||||||
∫ |
|
|
|
dx dx = |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
∫ |
с2 (x) |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
1 |
|
|
1 |
|
|
|
2 |
|
|
c′(x) |
|
|
|||||||
= |
|
|
|
+ ∫ |
|
|
|
|||||||||||||
|
|
|
∫ |
|
|
dx |
∫ |
|
|
∫ |
||||||||||
2 |
|
с(x) |
с2 (x) |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx 2 .
|
|
(43) |
|
1 |
|
|
|
dx dx dx. |
|||
c(x) |
|||
|
|
||
|
|
||
Внося (43) в (42), приходим к представлению частного решения в виде
|
λ |
|
2 |
|
|
|
1 |
|
|
2 |
|
|
|
|
|
c′(x) |
|
|
1 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
W = |
|
t |
|
+ ∫ |
|
|
|
dx |
|
|
+ λ∫ |
∫ |
|
|
|
|
∫ |
|
|
dx dx dx, |
|||||||||||
2 |
|
с(x) |
|
2 |
(x) |
c(x) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
с |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
или, с учетом тождества α2 + β2 |
= |
1 |
(α − β)2 + |
1 |
(α + β)2 , |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
||||
|
|
|
|
W = λ |
|
|
|
|
|
|
1 |
|
|
2 |
+ λ |
|
|
|
1 |
|
|
2 |
|||||||||
|
|
|
|
t |
− ∫ |
|
|
|
|
|
dx |
|
t + |
∫ |
|
|
dx |
+ |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
с(x) |
|
||||||||||||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
с(x) |
|
|
|
4 |
|
|
|
|
(44) |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
+λ |
|
c′(x) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
dx dx dx. |
|
|
|
|
|
|||||||||||
|
|
|
|
∫ |
|
|
|
|
|
∫ c(x) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
∫ с2 |
(x) |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Таким образом, получено точное решение волнового уравнения с произвольным переменным параметром с(х). На основании этого ре- шения нельзя строить общее решение волнового уравнения и, соот- ветственно, нельзя удовлетворить наперед заданным граничным и начальным условиям, но волны, описываемые формулой (44), вполне могут существовать в неоднородной среде с переменной скоростью распространения с(х). Причем важно подчеркнуть, что эти волны распространяются, не затухая, и в связи с этим они получили весьма характерное название – блуждающие волны.
Заметим, что аналогичное решение может быть получено и для трехмерного случая.
27
Библиографический список
1.Анго, А. Математика для электро- и радиоинженеров / А. Анго. –
М.: Наука, 1965. – 778 с.
2.Баскаков, С.И. Основы электродинамики / С.И. Баскаков. – М.: Советское радио, 1973. – 248 с.
3.Бреховских, Л.М. Волны в слоистых средах / Л.М. Бреховских. –
М.: Наука, 1973. – 513 с.
4.Цапенко, Н.Е. Аналитические функции и интегральные преоб- разования / Н.Е. Цапенко. – М.: Физматлит, 2012. – 244 с.
28

Учебное издание
Журавлева Ирина Евгеньевна Цапенко Николай Евгеньевич
УРАВНЕНИЯ МАКСВЕЛЛА И ПРЕОБРАЗОВАНИЯ ЛОРЕНЦА
Учебное пособие
Редактор И.Н. Машакина
Компьютерная верстка М.А. Шамарина
Подписано в печать 10.03.15 Электронная версия |
Уч.-изд. л. 1,8 |
Формат 60 × 90 1/16
Национальный исследовательский технологический университет «МИСиС», 119049, Москва, Ленинский пр-т, 4
Издательский Дом МИСиС, 119049, Москва, Ленинский пр-т, 4
Тел. (495) 638-45-22
Отпечатано в типографии Издательского Дома МИСиС 119049, Москва, Ленинский пр-т, 4
Тел. (499) 236-76-17, тел./факс (499) 236-76-35
29
