ответы механики сплошной среды

Билет №1

1. Предмет механики сплошной среды

Механика сплошной среды – наука о равновесии и движении деформируемых твердых тел, жидкости и газа. В механике сплошной среды рассматриваются тела с изменяющимися формами и расстояниями между точками. В механике к сплошной среде относятся как упругие и пластические, так и жидкие и газообразные тела. В механике сплошной среды разрабатываются методы сведения механических задач к математическим задачам.

Основные гипотезы мсс:

Гипотеза сплошности объекта. Тело как объект исследования есть непрерывная, сплошная среда, заполняющая некоторый объем или часть пространства. Эта гипотеза позволяет отказаться от молекулярно-кинетической теории строения вещества и применять аппарат дифференциального и интегрального исчисления.

Гипотеза непрерывности метрического пространства. Пространство, в котором находится объект исследования, есть бесконечная, непрерывная протяженность, обладающая свойствами трехмерности, однородности и изотропности. Эта гипотеза позволяет применять аппарат аналитической геометрии.

Гипотеза непрерывности абсолютного времени. Время, в течение которого наблюдается объект исследования, есть бесконечная, непрерывная, однородная длительность, которая протекает одинаково для всех наблюдателей. Эта гипотеза позволяет не учитывать эффекты теории относительности.

2. Нелинейные задачи неустановившихся движений со свободной поверхностью

Введем в

Билет 2.

1. Точки зрения Лагранжа и Эйлера на изучение движения сплошной среды. Уравнение неразрывности

Сплошная среда представляет собой непрерывную совокупность точек.

Скорость 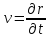. Кроме скорости требуется рассматривать еще ускорение точки сплошной среды, кот явл вектором, .

Первое основное дифференциальное уравнение механики сплошной среды, которое носит название уравнение неразрывности в переменных Эйлера

Билет 3.

1. Физические и математические основы движения жидкости в пористых средах. О фильтрационных аномалиях в пористых средах

Существуют молекулярно- поверхностные силы на границе соприкосновения

При движении жидкости в пористых средах следует учесть добавочные сдвиговые напряжения

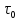
Численное интегрирование – это область приближенных методов вычисления определенных интегралов.

Билет 4.

1. Замкнутые системы механических уравнений для простейших моделей сплошных сред

2. Перемещение поверхности раздела между жидкостями разной плотности.

из ур-ния неразрывности получаем ,Подставляя в 7.4, получим систему двух нелин-х ур-й с частными производными.

Билет 5.

1. Некоторые сведения из тензорного анализа. Идеальная жидкость и газ

Тензор напряжений в идеальной жидкости задаётся одним числом р. Для идеальной жидкости – метрический тензор. Любой тензор Т, тензорная поверхность которого есть сфера, называется шаровым. Все шаровые тензоры имеют вид – скаляр.

2. Динамика грунтовых вод при поливах. Образование растекания бугров грунтовых вод.

Билет 6.

1. Линейное упругое тело и линейная вязкая жидкость.

Одними из частных сплошных сред, являются модель линейного упругого тела и модель линейной вязкой жидкости. Построение этих моделей прводится параллельно, так как способы их введения формально аналогичны. Эти 2 модели описывают два совершенно различных типа механического поведения реальных сред.

Раздел механики слошной среды, в котором изучаеется поведение сплошных сред, подчиняющихся закону Гука или более общему закону (2.1), носит название теории упругости, а раздел, в кот-м рассматриваются движения сплошной среды, подчиняющейся закону Навье-Стокса или более общему закону (2.2, 2.3) – теорией движения вязкой жидкости.

2. Движение с перетоками. Начально-краевая задача для движения с перетоками

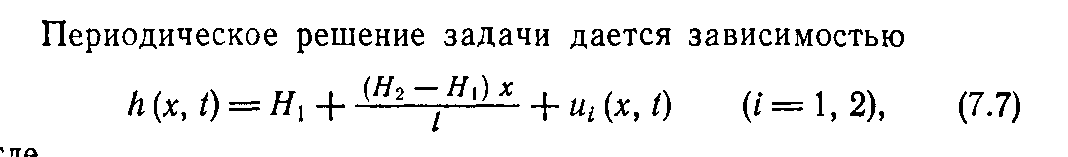
непрерывными.

билет №7

1. Основные понятия и уравнения термодинамики.

Термодина́мика — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии

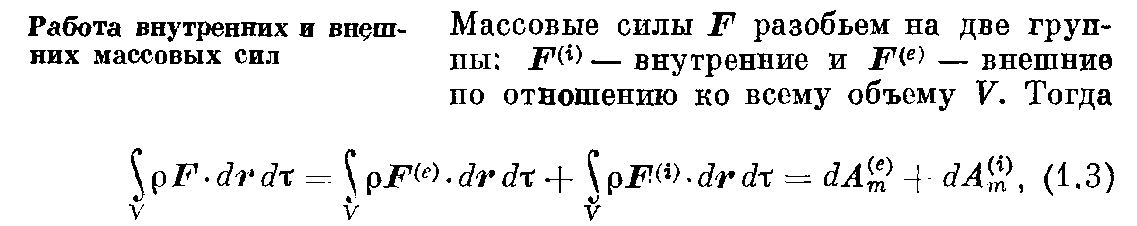
2. Статистический способ определения коэффициентов фильтрации и диффузии. Основные уравнения диффузии.

Билет 8.

1. Примеры идеальных и вязких сред и их термодинамические свойства.

А) Модель идеальной несжимаемой жидкости.

2. Метод конечных элементов для интегрирования уравнения неразрывности

условиям.

Разобъем всю область на треугольники, пронумеруем их. Обозначим значения h(x,y) . Получим основные уравнения метода конечных элементов для треугольной области и записываем их в матричной форме:

В выражении (7.3) для J(h) добавляется интеграл по контуру L, ограничивающему оббласть D: и ищется минимум такого расширенного функционала.

Билет №9

1. Теплопроводность. Теория моделей смесей жидкостей или газов с учетом химических реакций и диффузии компонент.

Билет №10

1. Моделирование смесей при обратимых процессах

Билет №11

1. Модели смесей с учетом необратимых процессов.

равновесным обратимым процессам. Допустим,

Билет 12.

1. Плоские движения в вертикальной плоскости.

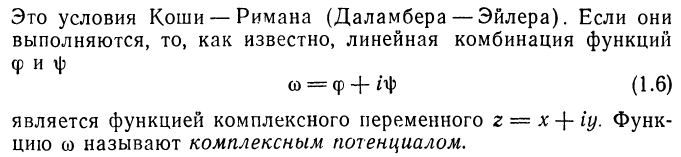
2. Вариационные методы в теории упругости и пластичности.

Вариационными методами наз-ся методы точного и приближенного решения задач, основанные на использовании экстремальных свойств некоторых функционалов. Рассмотрим ур-ние притока тепла для некоторого действительного процесса, проходящего через данное состояние покоя:

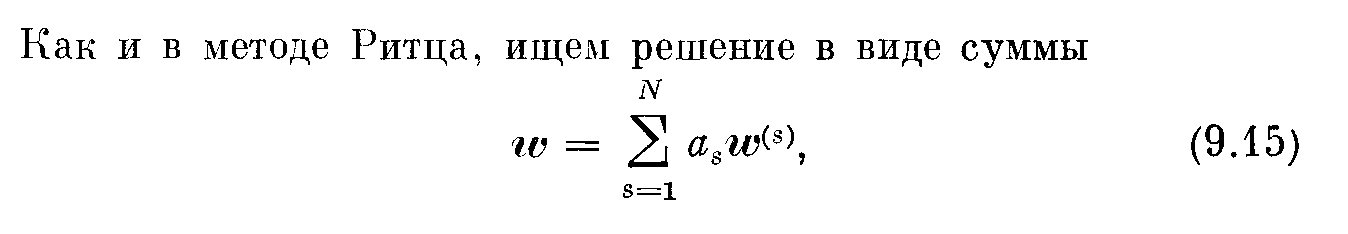
Билет 13.

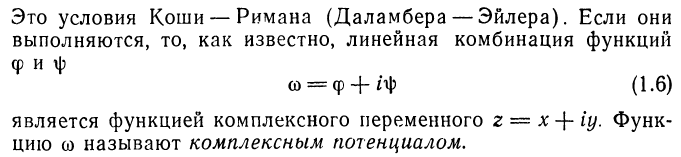
2.Модель упругого тела.

Все процессы деформирования упругих тел обратимы. Состояние малой частицы упругого

Например, св-ва симметрии кристаллов также можно задавать с помощью параметров , некоторые из которых могут быть компонентами векторов или тензоров. В распространенных классических вариантах моделиупругих тел принято, что в каждой частице

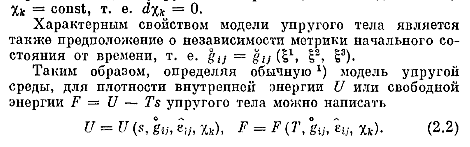
Билет 14.

1. Граничные условия в плоском установившемся движении

Различают 4 вида границ области движения:

1. Непроницаемые границы. Непроницаемые границы явл линиями тока, поэтому вдоль них ф-ция тока должна иметь постоянное значение. . Ур-ния (1) и (2)- характер-щее непроницаемую границу, м/о рассматривать как 2 усл., кот выполняются вдоль непр. границы.

2. Границы водных бассейнов. Предполагая, что водная граница представляет отрезок прямой будем рассматривать (3) и как два условия на границе водного бассейна.

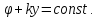3. Линии свободной поверхности представляют линии раздела между влажным и сухим грунтом. Здесь рассматривают 2 вида условий: 1) давление считают равным атмосферному. Получаем условие 2.)

4. Участки, где вода из тела плотины высачивается не в водный бассейн, а прямо в атмосферу наз-ся промежутками высачивания. Здесь выполняются усл-я:

2. Задачи теории упругости.

приложенных к упругому телу, в этом случае =0. В теории упругости рассматриваются и динамические задачи, например задача о колебаниях упругих тел. Примерами типичных статических задач теории упругости, которые отличаются друг от друга видом граничных условий, являются след-щие 3 задачи:

Билет 16.

1. Гидравлическая теория установившихся движений.

Под

виях и тд. Гидравлические теории дают хорошие результаты.

1. Принцип Сен-Венана

моментом этих сил и приближенно не зависят от детального характера распределения сил. Влияние деталей распределения сил практически сказывается только в непосредственной окрестности области их приложения.

Билет 17.

1. Гидравлическая теория и ее основные положения.

Под

виях и тд. Гидравлические теории дают хорошие результаты.

2. Методы сопротивления материалов в задачах об изгибе балок.

Метод сопротивления материалов дают возможность по известным суммарным характеристикам – перерезывающей силе и изгибающему моменту – определить распределение растягивающих и сжимающих напряжений и форму изогнутой ои балки. Поэтому важно знать величины М и Р в каждом сечении балки. Используя закон Гука для простого растяжения, для распределения получим ф-лу: Если растягивающая балку сила отсутствует, то ,или 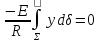. Зная напряжение, действующие в рассматриваемом сечении, можно вычислить изгибающий момент М:

Билет 18.

1. Свободная поверхность при инфильтрации и испарении.

В уравнении примем , но оставим , определяющее инфильтрацию или испарение. Перепишем 1.12 в виде . Интегрирование его дает

2. Примеры моделей пластических тел.

Билет 19.

1. Напорно-безнапорное движение

ными бассейнами гидростанции.

2. Задача о кручении цилиндрического стержня из упруго-пластического материала без упрочнения.

Билет 20

1. Движение в пластах с перетоками.

Пусть водоносный пласт с коэф-ом фильтрации к подсчитается слабо проницаемым гориз-ным

бит скважины совершенно определённый.

2. Напорно-безнапорное движение

ными бассейнами гидростанции.

МГЭ и МКЭ

Метод конечных элементов (МКЭ) — численный метод решения дифференциальных уравнений с частными производными, а также интегральных уравнений, возникающих при решении задач прикладной физики. Метод широко используется для решения задач механики деформируемого твёрдого тела, теплообмена, гидродинамики иэлектродинамики.

Метод граничных элементов для двумерной задачи.